广义分数阶Allen-Cahn相场方程的数值模拟研究
吴函宇 都昌发 刘雨婷 郑洲顺
(中南大学 数学与统计学院,长沙,410083)
1 引言
Allen-Cahn方程是相场模拟中描述非保守场变量的一类经典的高阶非线性偏微分方程,最初是由Allen和Cahn[1]在研究结晶固体的相边界运动时提出来的.Allen-Cahn方程及其衍生方程具有丰富的数学物理内涵和实际的应用背景,在图像处理、结晶和凝固过程、金属烧结过程、晶体生长过程等实际科学问题方面应用都非常广泛[2-5].
经典的Allen-Cahn方程本身具有诸多特性,在大多数情况下是无法得到其解析解的,因此构造高效的数值算法十分关键.一方面,Allen-Cahn方程满足一些特有的物理性质,如能量递减性,故如何构造出满足方程固有特性且能保证系统稳定的数值算法是我们要克服的难题.另一方面,Allen-Cahn方程中存在很强的非线性性,对非线性项进行处理从而构造高阶的算法也是我们要解决的难点.目前用于求解Allen-Cahn方程的数值方法主要有谱方法、有限差分法、有限元法、局部间断有限元方法和自适应有限元方法等[6-10].其中,Feng和Wu[10]针对Allen-Cahn方程的有限元逼近建立了一类残量型的后验误差估计,在此基础上提出了求解Allen-Cahn方程的自适应有限元算法.Feng和Prohl在文献[11]中一种求解Allen-Cahn方程的半离散格式和全离散格式,得到了先验误差估计,并证明了这两种格式分别具有最优阶的收敛误差.Lee[12]提出了一类简单且稳定的二阶算子分裂方法,该方法将Allen-Cahn方程分解成三个子方程来处理,且这三个子方程按照特定的顺序组合起来就可以达到二阶精度.Eyre[13]构造了一类具有一阶精度的非线性能量稳定的时间推进格式.在此基础上,大量能量稳定的格式被构造出来.Shen和Yang[14]构造了两类稳定化的分别具有一阶精度和二阶精度的能量稳定的半隐格式.Choi,Lee和Kim[15]提出了一类求解Allen-Cahn方程的无条件梯度稳定的格式.Feng[16]构造了能量稳定的一阶及二阶半隐半显格式.Zhang和Du[17]研究了一些能够保持数值稳定性及精度的时间推进格式.Wang和Yu[9]基于向后微分公式和Crank-Nicolson方法构造了两类求解Allen-Cahn方程的稳定的二阶半隐线性格式.
在对材料微结构演化的模拟中,虽然相场方法克服了描述突变界面的困难,但是传统整数阶的相场方法对于反常扩散现象或材料本身具有长时间的记忆效应等问题的描述和求解得不到好的效果,因此,引入分数阶相场去描述比传统整数阶相场更为适合.随着相场方法的广泛运用,将相场方程推广到分数阶也引起了国内外诸多学者的关注.其中,王宏等[8]研究了时空分数阶Allen-Cahn方程,时间上采用L1格式离散Caputo导数,空间采用配置方法,得到了该时间分数阶方程的离散格式,并通过不同的迭代方法比较了快速算法与直接求解的效率与收敛性.为了减少储存和计算量,张继伟等[18]研究了Caputo导数的一类快速算法,证明了提出的快速算法的稳定性,并通过数值算例验证了格式的准确性和低储存低耗时性.在此基础上,王宏等[19]研究了时间分数阶Allen-Cahn方程,构造了时间上采用快速Caputo算法,空间上采用Fourier谱方法的离散格式,并通过数值算例验证了其离散格式的准确性.沈捷等[20]引入了一个稳定项,使其与显式差分格式离散产生的误差同阶.这是一种基于差分方式的无条件能量稳定的数值格式.最近,汤涛等[21]首次证明了时间分数阶梯度流的能量耗散性,并采用稳定方法构造了一阶时间离散格式.
2 广义分数阶Allen-Cahn相场方程模型
由于分数阶微积分算子的定义比较多,例如Caputo,Riesz,Riemann-Liouville等[22],如何能得到一类能包含上述几种定义且更加一般的分数阶微积分算子的定义呢?上述疑问所概述的分数阶微积分算子我们称为广义分数阶微积分算子.当然广义分数阶微积分算子的种类也比较多,最早是由Agrawal于2012年提出的.在广义分数阶微积分算子的定义中,若引入尺度函数和权重函数,通过选定特殊的尺度函数和权重函数,则其可以退化为经典的Riemann-Liouville,Caputo,Hadamard和Kober等定义.在文献[23]中,作者指出尺度函数的出现将一致积分区间映射到非一致积分区间,权重函数表示在不同的时刻或空间位置给予不同的权重.尺度函数的作用考虑到了时间上的压缩和拉伸,确切地说,如果尺度函数是凸函数,数学上相当于将时间向终止时刻压缩,而将初始时刻进行拉伸,如果尺度函数为凹函数,则正好相反;而权重函数的作用则考虑到了不同时刻的物理量在研究范围内的比重.另外,在尺度函数取z(t)=t和权重函数取w(t)=1时,广义分数阶微积分算子便退化为经典的Caputo和Riemann-Liouville意义下的分数阶微积分算子.采用这种定义可以有效地求解一些积分方程,这也使我们可以从不同角度来了解分数阶微分方程.而广义分数阶Allen-Cahn方程和求解鲜见,因此把相场方程推广至更一般的广义分数阶方程还具有很大的发掘空间.
相场模拟运用于许多与材料微结构演化有关的实际问题中,比如晶粒的粗化与生长,铁电材料的相变和凝固现象等等.数学上通常用Allen-Cahn方程和Cahn-Hilliard方程来刻画这些过程.因此解决实际问题就可以转化成求解一个带有初边值条件的微分方程的问题.对于变系数非线性问题,则需要借助于数值方法来求解,主要有有限差分法和有限元法等等.实际问题中材料微结构演化时可能有多个场变量,客观地描述这些现象,需要分别在上述两个方程的基础上加上非线性项或某些参数.近年来,人们发现运用分数阶导数模型可以更好地描述某些特殊的扩散现象,因此出现了许多分数阶Allen-Cahn方程和Cahn-Hilliard方程.由于分数阶导数具有记忆性,通常这些分数阶方程的时间项导数都不再是一阶,而是介于0和1之间(次扩散),或者介于1和2之间(超扩散).时间分数阶导数意味着当前时刻的状态依赖于自初始时刻以来的全部历史状态.
本文研究如下形式的广义分数阶Allen-Cahn方程
(1)
其中,广义Caputo时间分数阶偏导数定义为
(2)
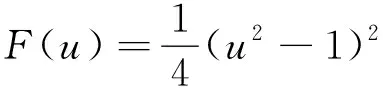
这个方程的一个重要特征是可以被看作是以下能量泛函的梯度流形式:
(3)
因为广义分数阶导数在特殊的情况可以退化为普通的分数阶导数和整数阶导数,因此研究这样更一般形式的Allen-Cahn方程显得很有必要,而且可以研究更一般情形下方程的解及其相性质.
3 广义分数阶Allen-Cahn相场方程的数值离散格式
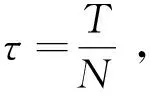
(4)
令ζ=z(s), 由z(s)的可逆性, 有s=z-1(ζ).对上述离散公式通过变量代换, 可以得到
(5)
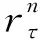
(6)
对于积分
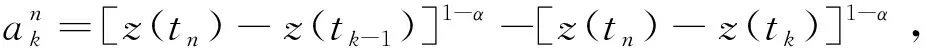
(7)
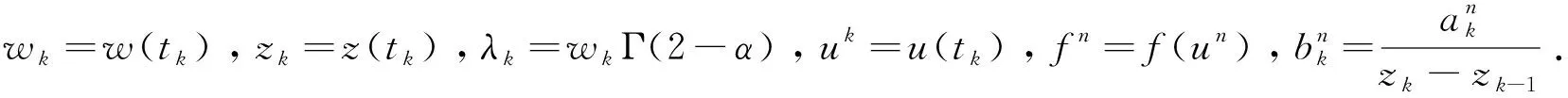
(8)
进而可得如下半离散格式:
(9)
下面我们采取有限差分方法对空间区域进行离散.记Δh为算子Δ的离散形式, 则对于一维和二维情形分别有
(10a)
(10b)
在时间半离散格式中用Δh代替Δ,得到方程的全离散格式,二维情形如下
(11)
在上式中忽略截断误差项,则可以得到如下数值格式
(12)
再加上相关的初值和边界条件,即可得到完整的数值离散格式.值得注意的是,由于非线性源项f(u) 的存在,使得求解过程中需要使用迭代方法,比如Newton迭代、Picard迭代等.当然也可以采用凸分裂技巧来处理.
4 广义分数阶Allen-Cahn相场方程的数值模拟研究
基于上一节构造的数值格式, 这一节我们结合具体的算例,重点关注不同相场模型的数值模拟.
4.1 一维Allen-Cahn相场方程的数值模拟
取定ε=1.2e-2,分别考虑不同的阶数α=1.0, 0.8, 0.6, 0.4和不同的尺度函数对演化过程的影响.初值u0=0.53x+0.47sin(-1.5πx),结果如图1所示.
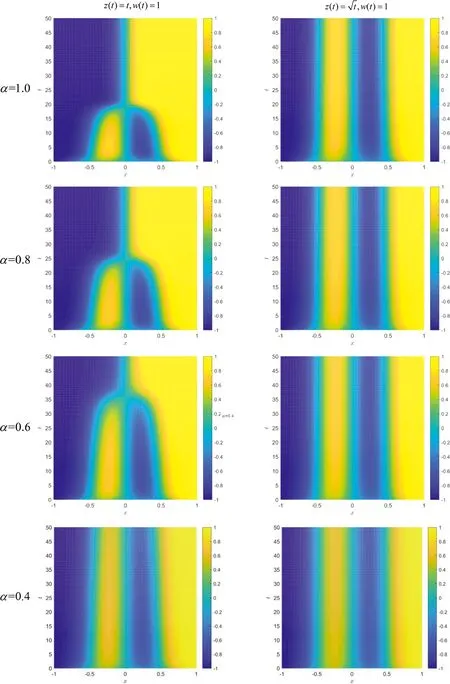
图1 不同尺度函数、权重函数和分数阶数对演化过程的影响
由图1可以看出,随着α的减小,相分离过程是在逐渐减慢的,而不同的尺度函数在相同的阶数下对相分离的速度也有一定的影响.
4.2 二维Allen-Cahn相场方程的数值模拟
4.2.1 随机初值
选择ε=1.0e-3,尺度函数和权重函数分别为z(t)=t,w(t)=1,这对应于普通分数阶的情形.我们选择带有扰动的初值来研究不同阶数对演化过程的影响:初值u0=cos(8πx)cos(8πy)(2rand(x,y)-1),其中rand(x,y)为[0,1]内的随机数,边界条件为Neumann条件,模拟结果如图2所示.
在图2中,对于上述四种情况,数值解在t=4之前看起来几乎相同,这对应的是相分离过程所需的时间.随着动力学进入长时间尺度的相粗化过程,数值解就开始不同了,进一步可以从能量演化图看出这一点.从数值上,我们可以得出结论:不同的分数阶具有相分离的相似动力学,但是随着分数阶阶数的减小,其对应的粗化动力学也逐渐变慢.
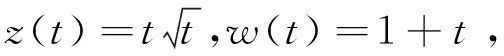
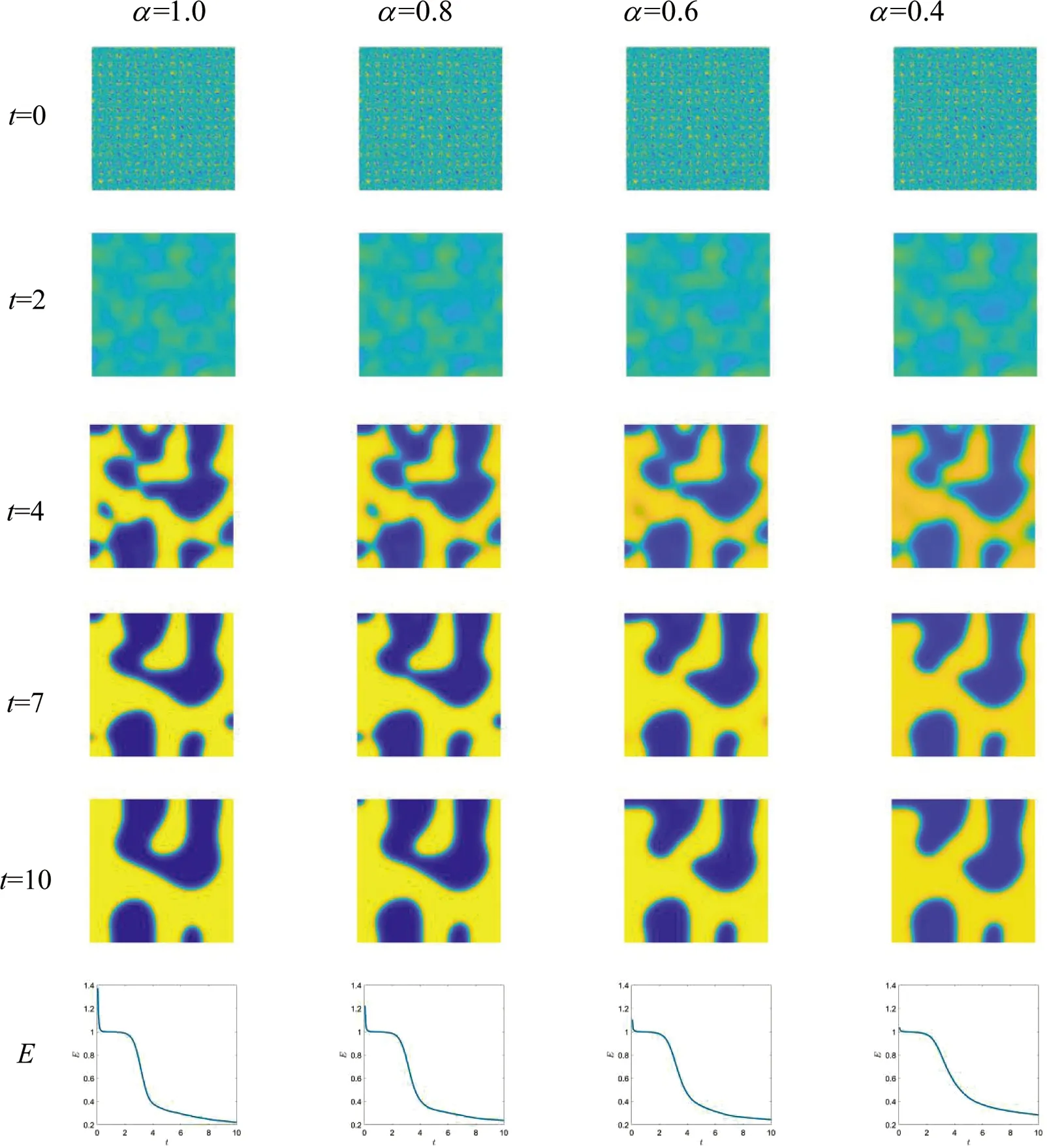
图3 不同分数阶数(广义分数阶)在演化过程中的影响
图3所示与图2情况类似.对于上述四种情况,数值解在t=4之前看起来几乎相同,同样,这对应的是相分离过程所需的时间.随着动力学进入长时间尺度的相粗化过程,数值解就开始不同了,进一步可以从能量演化图看出这一点.我们同样可以得出结论:不同的广义分数阶具有相分离的相似动力学,但是随着广义分数阶阶数的减小,其对应的粗化动力学也在逐渐变慢.
4.2.2 复杂初值情形
取定ε=1.0e-3,边界条件仍为Neumann条件,考虑如下两种初值:
(1)“哑铃”形状的初值u0:
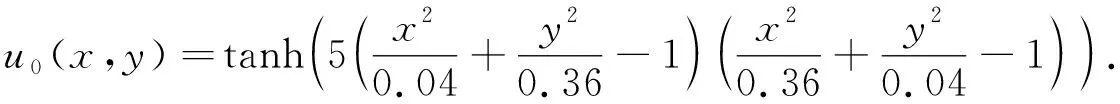
在普通分数阶和广义分数阶情形下的模拟结果分别如图4,图5所示.

图4 不同分数阶数(普通分数阶)在演化过程中的影响

图5 不同分数阶数(广义分数阶)在演化过程中的影响
从图4中可以看出,在普通分数阶情形下,随着时间的变化,α=0.5时的演化速度远小于α=1时的情形.其次能量均发生递减符合实际能量动力学的演化规律,但α=1时两相基本发生了完全的融合,能量也基本递减为0,而α=0.5时基本两相并未发生明显的融合现象,且能量递减的趋势也并不明显.
从图5中可以看出,在广义分数阶情形下,随着时间的变化,α=0.5时的演化速度远小于α=1时的情形.其次能量均发生递减,但α=1时两相基本发生了完全的融合,能量也基本递减为0,而α=0.5时基本两相并未发生明显的融合现象,且能量递减的趋势也并不明显.这与普通分数阶得到的结果一致,验证了从广义分数阶出发研究相场模型的有效性.
5 界面宽度ε对Allen-Cahn相场方程的数值解的影响分析
5.1 一维情形下,界面宽度变化对Allen-Cahn相场方程的数值解的影响分析
下面我们取初值u0=0.53x+0.47 sin(-1.5πx),研究不同的ε对不同模型的影响.结果如图6所示.
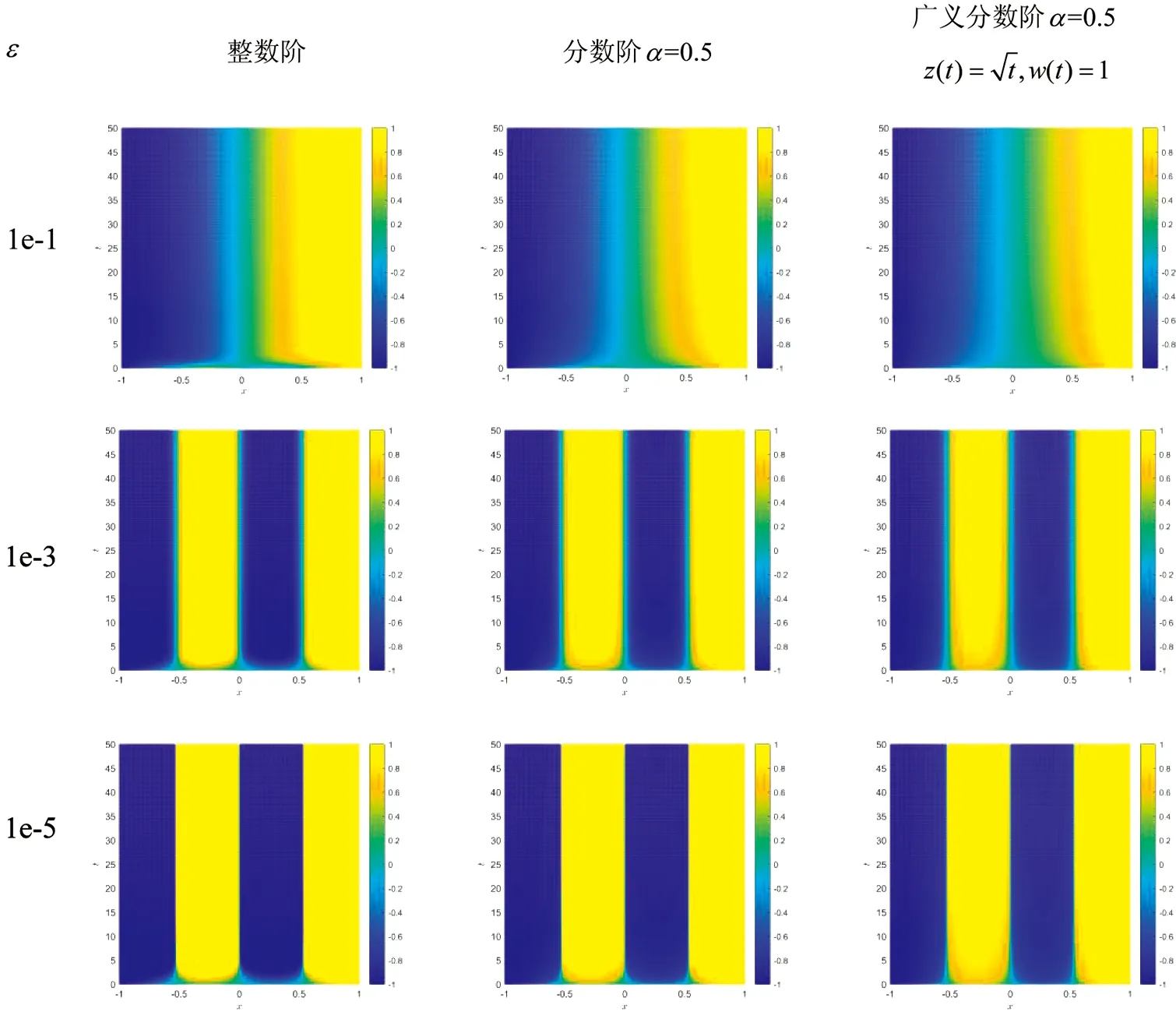
图6 不同界面宽度对不同的一维模型的影响
由图6可得,在同一阶数下,随着ε逐渐变小,相分离的速度也逐渐加快,这与ε的实际物理意义界面宽度在实际演化过程中对相分离的影响是一致的.
5.2 二维情形下,界面宽度变化对Allen-Cahn相场方程的数值解的影响分析
根据图7,我们可知无论是对整数阶、分数阶还是广义分数阶,随着界面宽度的变小,很容易得知演化速度越来越快,两相分离越快;针对同一界面宽度,广义分数阶的演化速度相较整数阶和分数阶较慢,但同样也达到了演化的效果,验证了从广义分数阶出发研究相场模型的有效性.
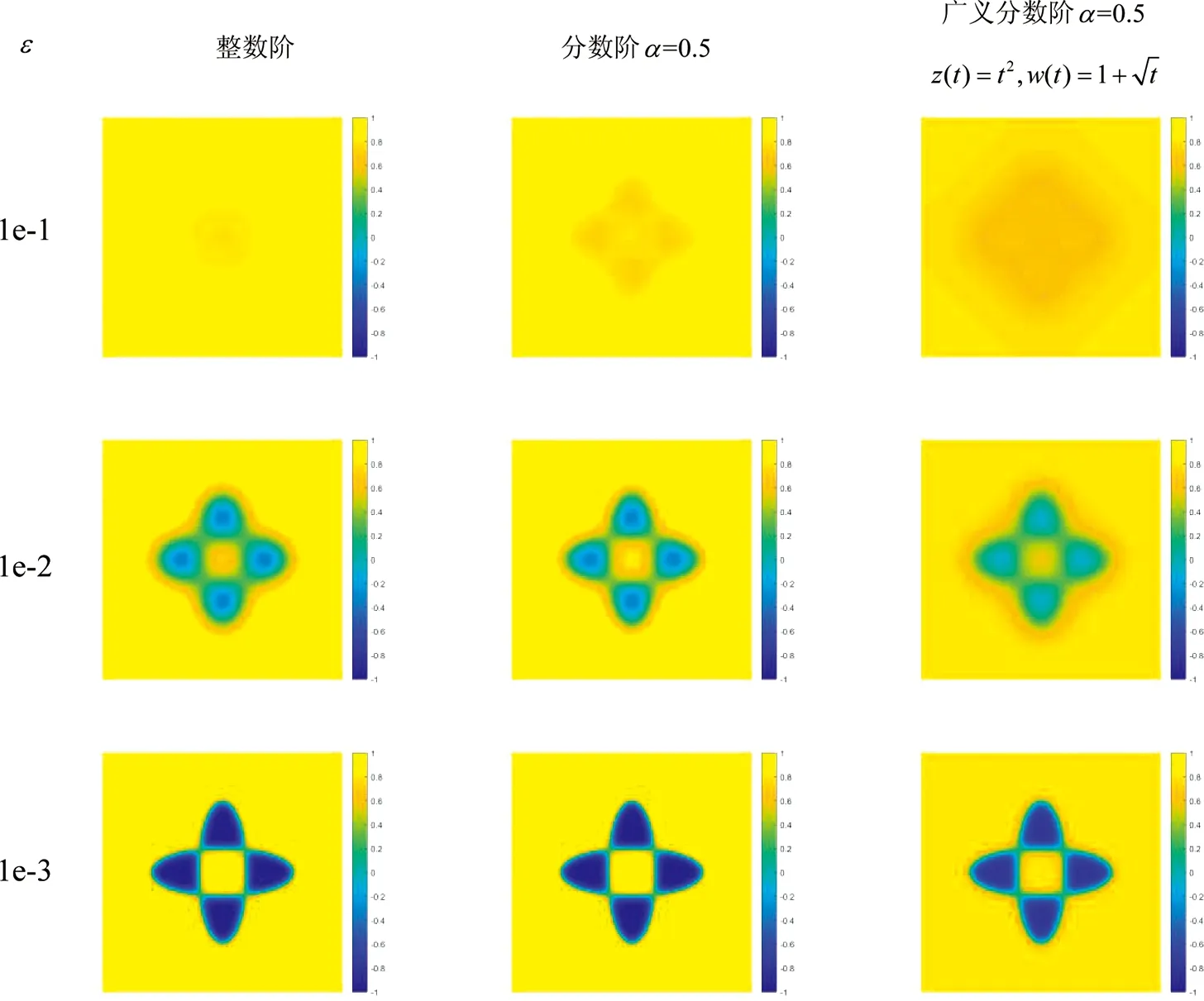
图7 不同界面宽度对不同的二维模型的影响(t=1时刻的演化结果)
6 结论
本文基于有限差分法研究和探索了整数阶Allen-Cahn方程的数值模拟方法,并将其推广至分数阶Allen-Cahn方程和广义分数阶Allen-Cahn方程,讨论了参数ε的变化对方程解的影响.
首先,采用了差分方法进行离散得到相应的离散格式,求解了整数阶Allen-Cahn方程,并用数值实验说明了该格式的有效性.
其次,将整数阶Allen-Cahn方程推广至分数阶和广义分数阶,分别给出了一维和二维的数值算例说明其相应的离散格式的有效性.
最后,基于数值方法分别分析了参数ε对整数阶Allen-Cahn方程、分数阶Allen-Cahn方程和广义分数阶Allen-Cahn方程解的影响,结果表明ε对方程数值解的影响与其实际物理意义界面宽度对材料微结构演化系统的影响是一致的.
- 数学理论与应用的其它文章
- GTH Algorithm, Censored Markov Chains, and RG-Factorization
- Multiplicity of Solutions for a Singular Elliptic System with Concave-convex Nonlinearities and Sign-changing Weight Functions
- Variants of Alternating Minimization Method with Sublinear Rates of Convergence for Convex Optimization
- A CCD-ADI Method for the Two-dimensional Parabolic Inverse Problem with an Overspecification at a point
- 鞅极大算子的一类四权弱型不等式
- Uniqueness on Recovery of the Permeability and Permittivity Distributions

