基于稀疏贝叶斯学习的煤岩图像识别方法

赵泽宾，孙 卓

（中国矿业大学（北京）机电与信息工程学院，北京 100083）

煤岩图像识别作为世界难题一直引起众多学者的关注，虽然现已提出多种煤岩图像识别方法，例如在计算机视觉技术方面，煤岩图像的纹理特征提取有小波变换法[1]，字典学习[2]，最大池化稀疏编码[3]等，但是这些方法都比较成熟而且已经发展到瓶颈。

目前煤岩识别技术主要分为物理探测技术和基于图像识别的多信息融合技术。近年来，最初作为机器学习算法的稀疏贝叶斯学习不仅继承了贝叶斯模型完善的理论基础，而且克服了其计算复杂度较高的不足，成为了众多学者的研究对象。由于稀疏贝叶斯学习能够充分的挖掘和利用数据的先验信息，并且可以得到信号和图像的稀疏表示，成功的被引用到信号处理和压缩感知领域[4,5]。为了将稀疏贝叶斯学习算法运用到煤岩图像识别领域，笔者采用该算法提取煤岩图像的纹理特征，通过迭代更新并趋于收敛的相关参数和最优权重对测试样本进行分类识别，来解决煤岩图像识别问题。

1 SBL算法基本原理

稀疏贝叶斯学习是稀疏信号重构的方法之一，其性能相当于重加权的范数恢复方法，并且不需要设置正则化参数[6]。稀疏贝叶斯学习的主要思想可以分为三步，首先获得先验概率和条件概率密度参数表达式，然后结合总体和样本，利用贝叶斯公式求得后验概率表达式，最后通过后验概率的大小进行统计决策。

1.1 基本模型

首先通过压缩感知的基本模型观测一个向量：

其中：为N×M的感知矩阵，它的列向量对应M个基向量；为N×1维压缩信号；为M×1维解向量，为未知的噪声向量。因为对于概率模型的训练过程实际上就是参数估计的过程，故：

式（3）反映了从先验分布到后验分布的转化。其中p(x)为先验分布，表示观测之前的概率；p(y)表示“证据”因子；是解向量x相对于其压缩信号的似然分布，在求最大似然估计的时候就是用该概率形式；被称为后验密度函数。然而在现实应用中，后验分布很难直接算出，但是通过贝叶斯定理可以将估计后验分布的问题转换为基于数据集来估计先验分布和似然。

通常在SBL算法中，把噪声v假设为高斯白噪声向量来处理，即v服从均值为0，σ2I方差为的高斯分布：

大部分情况下，σ2参数需要通过数据训练而得出。SBL要解决的问题是根据已知的A和y估算出未知解向量x，其实就是稀疏信号重构的过程。

1.2 推导过程

SBL算法在先验参数的结构下，采用了神经网络中常用的自动相关决策理论移除不相关的点来获取稀疏解。假设解向量的先验分布服从参数化的均值为0方差为α的高斯分布：

其中，解向量 x 的参数向量 α=(α1,α2,…αM) 是由超参数组成的向量。根据ARD可进一步表示，x的每个元素xi都服从一个参数化的且均值为0方差为αi-1的高斯分布[7]。因为假设噪声向量V符合均值为0，方差为σ2I的高斯分布，故可以得出压缩信号y符合均值为Ax，方差为σ2I的高斯分布，即似然分布为：

在贝叶斯框架下对参数加以先验分布，起到很好的约束作用，从而避免了模型中参数的数量和样本的数量一样多所造成的严重过匹配的问题，故假设模型中参数向量α和噪声参数σ2服从Gamma先验概率分布：

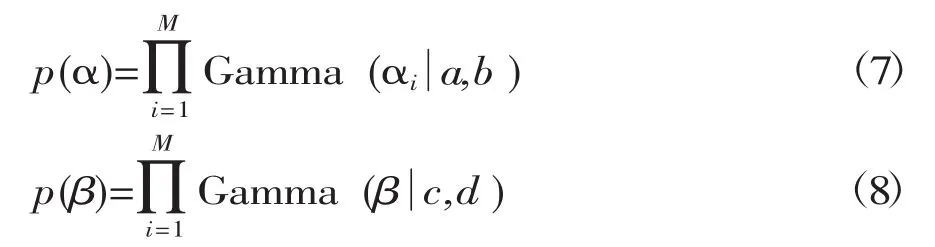
其中β=σ-2，再一次的说明稀疏贝叶斯学习对数据有着优秀的数据挖掘能力。

利用全概率公式对权值进行积分即可得出第二类似然函数表达式：

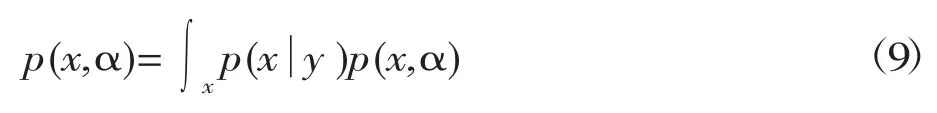
将式（5）和（6）代入到（9）可得：

其中，Γ=diag(α)。通过进一步计算可以得出：

其中：C是一个常数。此式我们可以得出p(x,α)是一个均值为0，协方差矩阵为Σv=σ2I+AΓ-1AT的高斯分布。

根据贝叶斯定理可以得出解向量的后验分布为：

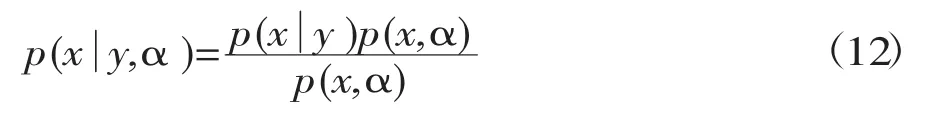
上式分子部分是两个高斯函数的乘积，根据高斯函数的相关性质可知，其乘积结果当然也是高斯函数，再结合分母部分也是服从高斯分布的，所以解向量的后验分布服从高斯分布，故将公式（5）、（6）和（9）代入（12）可得出：

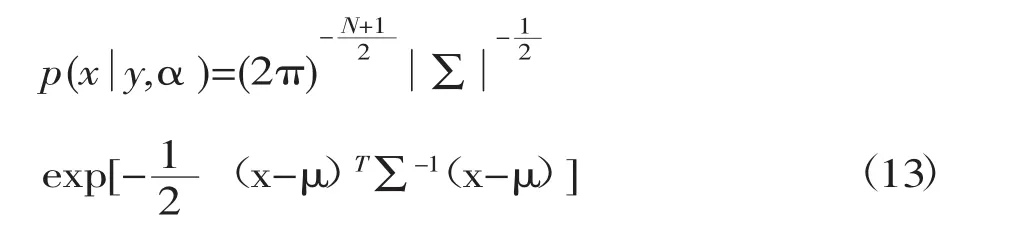
其中 μ=A（ATA+σ2Γ）-1ATy,Σ=(σ-2ATA+Γ)-1。μ 表示此高斯分布的均值，通过指数部分对x的一阶导数零点求得，协方差矩阵Σ为指数部分对x的二阶导数的逆。故解向量x的最大后0验估计由这个高斯分布的均值μ给出。而笔者要做的事情就是通过该模型寻找煤岩图像识别的新方法，提高煤岩识别率从而应用于实际的生产过程中。

1.3 线性回归与分类

贝叶斯线性回归是经典的线性回归方法之一，对数据有自适应能力，可以重复的利用一定数量的实验数据，并防止过拟合。对于本模型对应的似然函数可表示为：

回归的目的就是根据上式对x和σ2作出最大似然估计，从而找到解向量x=(x1,x2,…xM)中少量的非零元素。对式（12）中第二类最大似然函数求关于参数α和σ2的偏导并令其等于0进行求解，可以得出本模型的参数更新公式为：

其中：γi=1-αiΣii。在该算法的学习过程中，每次运算都会更新统计量μ和Σ，并代入式（16）和式（17），通过不断重复的计算使超参数α和σ2达到最大的迭代次数或者满足收敛条件[8-10]。

2 煤岩图像的识别

2.1 样本采集

实验选择110张页岩和砂岩图片作为岩石样本图片，再选择110张烟煤和无烟煤图片作为煤层样本图片，每类各55张，共计220张。每张图片的大小为48×48，格式为jpg，灰度级为256。

2.2 环境测试

从四类图片中各随机选出42张图片，共计168张作为训练样本，剩下的52张作为测试样本。并且各类图片均来自矿井下不同时段不同光照强度的现场图片，window环境下在MATLAB R2013b软件上进行实验。

2.3 特征提取与分类

煤岩图像的特征提取过程，其实就是该模型解向量的求解过程，说到底还是参数和迭代更新的过程。首先对样本图片进行预处理，其目的就是为了减少训练样本中的冗余信息，达到降维效果；然后利用稀疏贝叶斯学习算法进行模型的参数训练；最后根据稀疏贝叶斯分类模型对测试样本的分类识别。表1展示了使用和不使用SBL算法的识别率对比。

表1 稀疏贝叶斯学习对识别率的影响Table1 Impact of sparse Bayesian learning on recognition rate

3 总结

1）基于稀疏贝叶斯学习的煤岩图像识别方法大大增加了煤岩图像的可区分性，错误样本数从19个降低到2个；

2）该SBL算法将噪声干扰考虑在内，可以很好的解决矿尘等对煤岩图像的干扰；

3）该SBL算法可以为煤岩自动识别技术提供新的解决思路；