基于智能手机立体影像的稠密三维重建

张宁，王竞雪，2

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.西南交通大学 地球科学与环境工程学院，成都 610031)

0 引言

随着计算机视觉与数字图像处理技术的飞速发展，基于影像三维重建成为众多学者研究的热点问题[1]，并且已经应用到机器视觉[2]、游戏人物建模、生物医学[3-5]、考古[6]、火灾灾难现场还原[7]等领域，但是传统的三维重建方式是以工业相机拍摄带重建物体的表面纹理图像，通过匹配等工作进行三维重建，此方式操作复杂，对技术要求较高，并且重建的点云数目较为稀疏。曾昭鹏等[8-10]已经实现了手机图像的三维重建，但是文献[8-9]重建出的点云数目较为稀疏，不足以看出待重建物体的纹理细节信息，而文献[10]重建虽然可以看见纹理，但是并不清晰，而且仅仅适用于较为平整的场景。伊璐等[11-13]采用序列图像进行三维重建，并且获取了较好的实验效果，但是由于参加计算最终点云的图像数量较多，对计算机的要求较高，故不具有普适性。因此，为实现利用少量手机影像即能得到稠密的三维点云、简单易行的操作流程、良好的视觉效果，并且具有普适性的基于手机影像的三维重建，本文提出了一种基于智能手机立体影像的稠密三维重建方法，该方法对摄影设备要求较低，适用于不同的场景，重建点云稠密，并且有着良好视觉效果。

1 算法原理

本文提出一种基于智能手机立体影像的稠密三维重建方法：首先利用黑白棋盘格拍摄影像对相机进行标定，获取畸变系数和相机内参数；然后利用标定后的相机对重建物体进行拍摄，获取立体像对，并利用畸变系数对其进行影像初校正；在此基础上，结合SIFT匹配算法和RANSAC算法，提取初始可靠同名点，用于后续匹配及三维重建的参数计算。在密集匹配阶段，利用初始同名点，构建初始同名三角网，以三角形重心作为匹配基元，迭代匹配直到三角网达到一定的密集度。最后,结合相机内、外参数，利用三角测量原理对密集匹配得到的同名点进行计算，得到物方稠密三维点云。该方法总体流程图如图1所示。

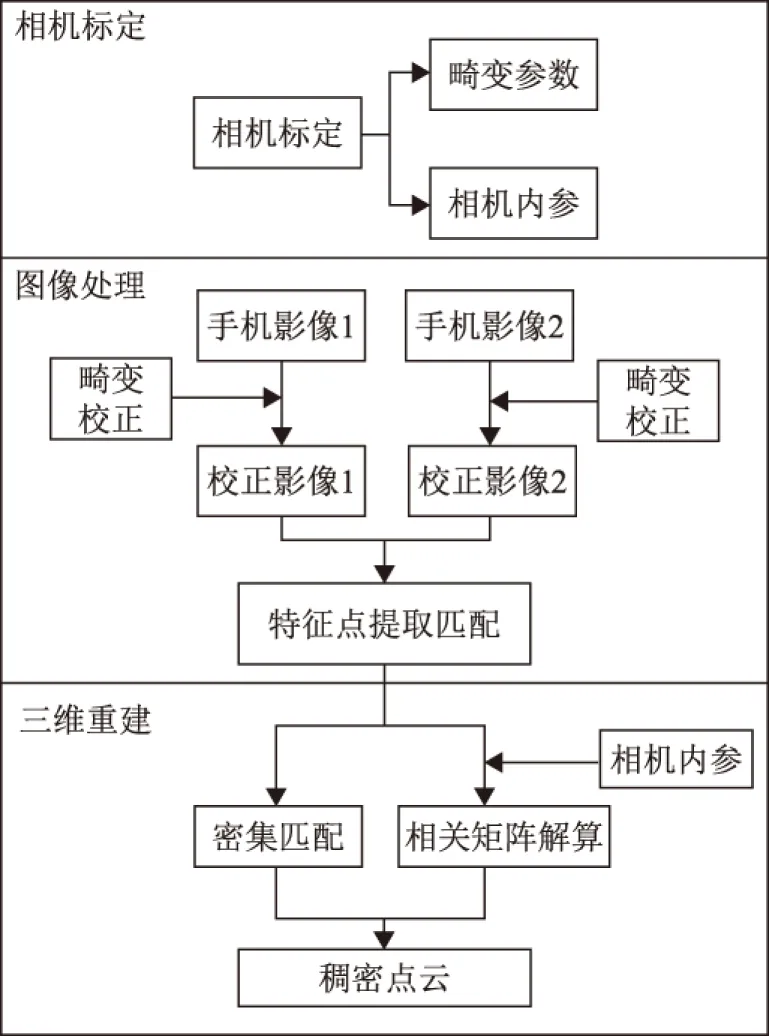
图1 基于智能手机立体影像的稠密三维重建总体流程

1.1 相机标定

相机可以将三维世界中的坐标信息映射到二维图像平面，该过程可以用简单的针孔模型进行描述[14]。假设空间点P在世界坐标系中的坐标为(XW，YW，ZW)，在相机坐标系中的坐标为(XC，YC，ZC)，在像平面坐标系中的坐标为(X，Y)，在像素坐标系中的坐标为(u，v)，针孔相机成像模型如图2所示。

图2 针孔相机成像模型

世界坐标系转换到像素坐标系的表达式如式(1)所示。

(1)

其中，K、H表达式如式(2)所示。

(2)

我们称K为相机内参矩阵，H为外参矩阵。公式(1)代表针孔成像模型中理想情况下的像素点与对应空间点的对应关系。然而，由于相机镜头的设计、制作工艺和安装等步骤中出现了错误，就不可避免地产生了畸变，从而公式(1)不能准确地表述该种关系，所以要对这些畸变进行校正。若求解出相应的畸变系数distortion，则可以尽可能地改善这些负面影响，进而达到校正影像的目的。

求解相机内参矩阵、畸变系数和相机外参矩阵的过程称为相机标定。本文采用张氏相机标定法对相机进行标定。由于不同的相机位姿对应着不同的相机外参，所以在该步骤获取相机内参K及其畸变系数distortion即可。

1.2 图像处理

本文对待重建的物体拍摄多张影像，在其中选择拍摄效果较好的2张影像作为三维重建的立体影像。再由上文得到的相机畸变系数对立体影像进行畸变校正。得到校正后的立体影像后，采取SIFT(scale invariant feature transform)算子进行特征点的提取匹配[15]。采用RANSAC算法对同名点进行错误点去除，得到高精度的同名点坐标，为得到可靠的基础矩阵F做数据准备，同时为密集匹配步骤提供更加准确、稳定的匹配基础。

1.3 三维重建

1)对极几何。对极几何的含义是：在一个物体的2幅图像中，匹配点的相对位置受到2个图平面空间几何关系的约束，这种约束关系在计算机视觉中被称作是对极几何关系。而基础矩阵F可以表示这种关系[16]。

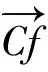
F=K-TEK-1；(f′)TFf=0

(3)

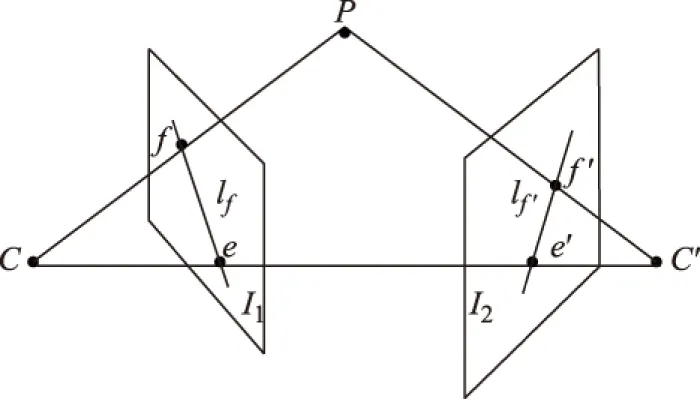
图3 对极几何示意图

进一步可以得到式(4)。

E=KTFK

(4)

将同名点带入公式(3)，并利用归一化八点算法求得基础矩阵F。因为基础矩阵F的秩为2，并且它有7个自由度，所以至少需要7个同名点对进行求解。在使用归一化八点算法得到的基础矩阵往往会因为噪声等原因导致基础矩阵的秩不为2，所以本文利用SVD分解法强行加入秩为2的解，具体办法如下所示。

①将同名点分别设为X=(x，y，1)T和Y=(x′，y′，1)T，根据公式(3)可得式(5)。

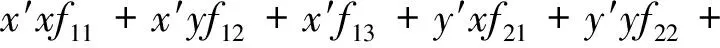
(5)

即(x′x，x′y，x′，y′x，y′y，y′，x，y，1)F=0。

②设F=USVT，对其进行SVD分解后得到U，S，V。

③得到的S=diag(s1，s2，s3)，且s1≫s2≫s3，所以将s3设置为0，S′=diag(s1，s2，0)。

④令US′VT=F′，此时F′即为所求。

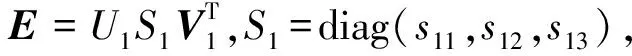
4)密集匹配。采用文献[17]算法，对立体像对进行密集匹配。该算法基本原理如下：在本文初始匹配得到同名点的基础上，利用RANSAC方法剔除误匹配点，并进行目视检测，以剔除误匹配的同名点，进一步提高初始同名点对的可靠性和准确性。文献[17]密集匹配采用迭代的思想，初始同名点的精度不高会造成后续迭代加密过程中误差传播。利用正确的同名点构建同名三角网，初始的匹配基元是三角形重心，结合极线约束、同名三角形约束、相关窗口灰度相关约束，匹配确定同名匹配点。如果上述过程未匹配到同名点，则计算待匹配同名三角形的相似度。如果三角形相似度满足设定的阈值，则利用仿射变换及其重心约束来确定最终同名点的坐标位置。加入同名点，更新三角网。重复上述步骤，直至三角网内所有三角形的面积小于一定阈值或没有新的同名点产生，则停止迭代，最终得到密集匹配的密集同名点。

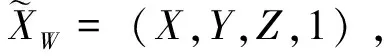
(6)

由图2可知，每一对同名点及其所对应的相机光心反向射线可以在空间中相交于一点，但由于噪声等因素的影响，在实际情况中很难交汇于一点，所以采用最小二乘法，计算同名点对应在空间坐标系中的三维坐标。对密集匹配后的同名点逐一进行计算，并根据同名点所对应在影像中的RGB三通道分量，分别对点云坐标进行渲染，最终得到具有RGB三原色的稠密三维点云信息。

2 实验结果与分析

实验过程中影像获取设备为VIVO X7手机，所摄像片大小为3 120像素×4 160像素，实验平台采用Intel(R) Core(TM) i5-4590 CPU @3.30 GHz，运行内存4 GB，Windows 10 64位操作系统。采用张定友相机标定法，得到手机摄像头内参矩阵K、畸变系数distortion和平均重投影误差(mean reprojection error，MRE)，如式(7)所示。

distortion=[0.099 646 5，-0.177 191 025，0，0，0]

MRE=0.374

(7)

本文平均重投影误差0.374较文献[8]中的平均重投影误差0.39更小。经过分析认为，该重投影误差较小的原因是：在将多张标定板像片进行相机标定时，删除了重投影误差较大的标定板像片，最终留下了12张存在各个方向上且重投影误差较小的标定板像片。

利用VIVO X7手机分别对内墙角、外墙角、石头、墙面4个特征地物进行拍摄，4种特征地物均有不同的纹理细节，以便检验本文稠密重建方法与传统重建方法重建结果的差异。获取4组立体影像用于验证本文方法。其中拍摄获取的原始影像与校正影像分别如图4、图5所示。

图4 原始图像

通过初始同名点计算得到相机投影矩阵P1，P2，如表1所示。本文将4组不同场景的手机立体影像分别以传统重建方法和本文重建方法进行三维重建，重建的三维点云数目统计见表2，统计图见图6。传统方法点云重建成果及本文方法点云重建成果见图7。在图7中：第一列为初始同名点三维重建得到的三维点云，即传统方法重建得到的三维点云主视方向观察图；第二列为本文方法重建得到的三维点云俯视方向观察图；第三列为本文方法重建得到的三维点云主视方向观察图。

图5 校正图像

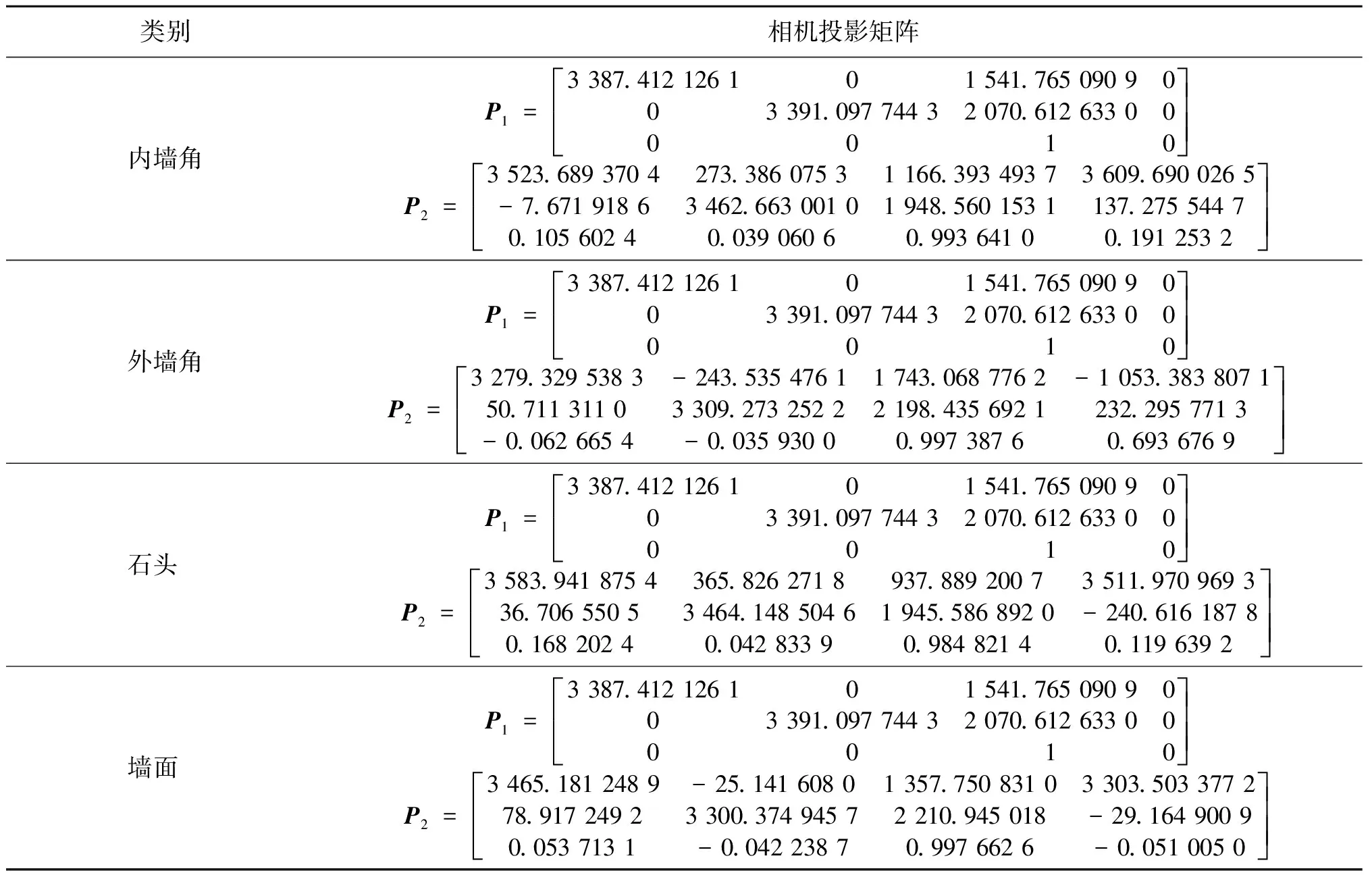
表1 相机投影矩阵

表2 点云数目 个

从表2分析可以得出，针对4组实验影像本文重建方法生成点云数目较传统重建方法生成点云数目分别增加了11倍、10倍、13倍、338倍，远远大于传统方法所重建的点云数目。而在图6统计图可以直观地看出2种重建方法在点云数目上的巨大差距，传统方法重建点云数目与本文方法重建点云数

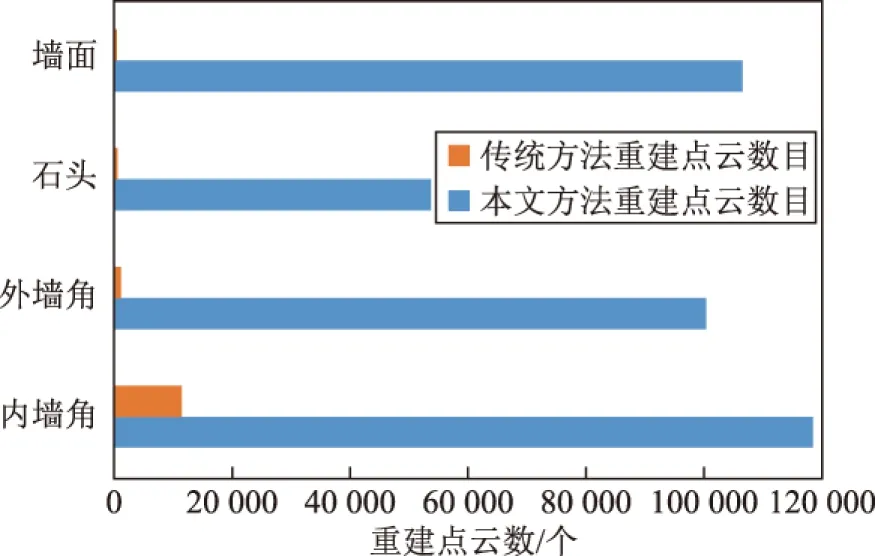
图6 点云数目统计

目相差了几个数量级。巨大的点云数目差异直接影响了点云的重建效果。由图7中的4组实验结果可以看出，本文重建方法得到三维点云效果要优于传统的重建方法，无论是在点云的纹理细节、视觉效果，都可以看出传统重建方法与本文重建方法的巨大差距。在图7第一列传统方法重建图中，除“内墙角”的实验结果外，其余实验结果均无法看出重建物体的轮廓与纹理细节，而且内墙角影像传统方法的重建结果仅可以看到重建地物的大致轮廓，但是纹理细节、效果均不如本文方法。本文提出的三维点云重建方法在4组实验中均没有出现较大误差，在不同的场景中表现出了较为良好的适应性，验证了本文方法的可靠性和鲁棒性。

图7 重建结果

3 结束语

针对传统立体影像三维重建对技术设备要求较高、重建三维点云稀疏、视觉效果不佳且不具有较好的场景适应性等问题，提出一种智能手机立体影像的稠密三维重建方法。该方法原理简单，通过在传统方法基础上增加了密集匹配步骤，大大提高了三维点云的稠密度，场景适应性强，视觉效果好。但该方法受初始同名点分布的影响，对立体影像重叠范围内同名点未覆盖区域未能实现三维重建，并且对于存在重复纹理的影像，初始点云精度对最终的重建结果影响较大。后续将进一步对上述2个方面进行深入研究。