基于像差特征分析的变焦光学系统装调

赵 岳，李 华，康世发，秦 星，郭惠楠

（中国科学院西安光学精密机械研究所，陕西 西安 710119）

引言

为保证在连续变焦过程中获得目标区域的图像清晰一致，使变焦系统在长短焦极限位置均具有较高的调制传递函数[1-4]，对光学系统的装调提出较高要求。目前，常用的装调方法有两种：一种是以光学定心加工为基准，根据平行光管星点像的状态，通过调整光学元件的不同空间姿态完成装调；另一种是以调焦组的入射光线光轴为基准，依次对变倍组、补偿组及后固定组完成共轴调整[5]。由于上述过程中光学元件数量较多，无法对光学系统中各光学元件的空间姿态进行量化，且装调周期长，装调精度低，已不再满足现阶段的装调需求。如何在变焦系统装调过程中定位影响像差的光学元件空间姿态，以及确保光学元件具有较高的共轴精度，是一项非常有价值的研究课题。

1 变焦光学系统初装调

1.1 光学系统描述

本文所研究的变焦光学系统，通过机械补偿法来降低像差的影响[6-8]。该系统由4 个不同组元相互作用完成成像，包括前固定镜组、变倍镜组、补偿镜组和后固定镜组。在成像过程中前固定镜组完成对光线的汇聚，为后面的变倍镜组提供参考目标；变倍镜组做线性运动，完成系统焦距的变化；补偿镜组通过光杆直线导轨实现与变倍组的相对运动，用以补偿运动过程中的像面位移。后固定镜组则是将补偿镜组所成物像汇聚在探测器靶面上，如图1所示。

光学性能指标要求该系统焦距为13.8 mm～280 mm，像元大小为3.45 μm×3.45 μm，相对孔径为1/2.4～1/6.23。装调完成后要求空间频率140 lp/mm 时，长短焦中心视场传递函数值分别大于0.45 和0.55，长短焦轴外0.7 视场传递函数值分别大于0.25 和0.35，变焦全程光学系统相对畸变优于3.2%。为达到上述要求，需要严格保证系统的光轴一致性。

图1 变焦光学系统Fig.1 Zoom optical system

1.2 变焦光学系统初装调

首先需要对光学元件完成微应力装调，通常使用Zygo 干涉仪将其面形控制在RMS≤ 0.025λ，减小面型对像散等像差的影响。

光学系统中各光学元件的空间姿态是影响该系统成像质量的主要因素，采用光学定心加工技术[9]，对微应力光学元件共轴精度进行有效控制，保证各光学元件间同轴精度在0.01 mm 以内，上下配合端面平行差 ≤0.005 mm。为了降低变焦光学系统的球差，要求调焦组和后固定组中各光学元件空气间隔公差 ≤±0.01 mm，变倍组与补偿组中各光学元件空气间隔公差 ≤±0.02 mm，变倍组中销钉中心与胶合镜2 的间隔公差 ≤±0.015 mm，补偿组中销钉中心与透镜7 的间隔公差 ≤±0.015 mm。

使用1 m 焦距平行光管对变焦系统在长短焦位置时的3#鉴别率板及 φ0.10 mm 星点像进行目视检测，所得鉴别率板图像锐利度较高，星点像较圆整。为量化光学系统指标，使用传递函数仪进一步检测，结果如表1所示。从表1可以看出，系统长短焦焦距满足设计要求，但长短焦传递函数MTF低于技术要求，表明初装完成的光学系统内部存在一定的像差，需要做进一步分析与调整。

表1 光学系统检测结果Table1 Detection results of optical system

2 CAA 技术在变焦光学系统装调中的应用

由图1可知，该变焦系统由多个组元构成，装调过程不可避免会引入人为误差，使光学系统不再具有对称性，从而产生各类像差。每一光学元件对于像差的影响各不相同，在装调过程中需要控制的变量也相对较多，增加了判断像差敏感元件的难度，降低了装调效率。本节在像差检测的基础上，使用CAA 技术，根据敏感元件的分布，完成对影响像差敏感元件的定位工作。

CAA（computer aided alignment）技术是指光学系统的计算机辅助装调[10]，是一种针对传统光学系统装调过程中出现的光学元件空间姿态不可控、无量化、随机因子影响大等缺点提出的一种新方法，通常应用在离轴三反光学系统的装调中。CAA 技术的核心是对光学系统中光学元件空间姿态进行量化及控制，其主要方法首先是使用干涉仪对光学系统进行波像差检测，然后根据检测结果及光学系统中心偏测量结果，进行Zemax 或CodeV 软件仿真，从而得出各光学元件的空间姿态位置及其调整量。最后通过使用各种调整工装，使各光学元件的空间姿态趋近于理论分析结果，从而完成光学系统装调。

2.1 变焦光学系统像差检测

由定义可知，波像差是实际波面与理想波面之间的光程差。当光学元件面形或空间姿态发生微量变化时，便会引入波像差，导致成像质量发生相应变化，进一步表现为MTF 指标不达标。对于精度要求较高的光学系统，通过定心加工校正各元件同轴度后，在系统装调中由于人为因素的存在，仍会引入装调误差，即光学元件偏心与倾斜，均会对该光学系统彗差、像散、场曲和畸变产生相应的变化[11-12]，但是不会对系统的球差产生影响。因此在精密光学镜头装调过程中必须保证光学系统的共轴精度，消除由光学元件偏心或倾斜所造成的像差。针对上文初装后检测结果，采用Zygo 干涉仪对其光学系统波像差进行检测，原理如图2所示。

对初装完成的变焦光学系统进行波像差检测可知，在短焦极限位置的像散为0.013 λ，彗差为1.282 λ，球差为0.005 λ；在长焦极限位置的像散为0.014 λ，彗差为1.882 λ，球差为0.005 λ。由此可见，彗差是该系统主要的像差，是造成变焦光学系统长短焦MTF 不达标的主要因素。

图2 干涉仪检测镜头波像差示意图Fig.2 Schematic diagram of wave aberration testing by interferometer

2.2 变焦光学系统彗差敏感光学元件分析

为了进一步有效定位产生彗差的光学元件，对变焦光学系统在长焦极限位置进行中心偏检测，结果如表2所示。

表2 偏心检测结果Table2 Results of eccentricity detection

图3为变焦光学系统中光学元件在不同情况下偏心及倾斜对彗差的影响变化。结合现有装配精度，使用CodeV 软件仿真建模，得到光学元件敏感等级由高至低分布（1～10）及相应MTF 变化量，结果如表3所示。由此可知，胶合镜1、透镜2、透镜5、透镜7 以及透镜10 的不同空间姿态是变焦光学系统产生彗差的主要因素，即为该系统产生像差的敏感光学元件，需要做针对性调整。

根据逆灵敏度公差分析方法[13-14]，将上述变焦光学系统中心偏检测结果带入CodeV 软件中构建正态分布模型并进行蒙特卡洛模拟仿真[15]，确定误差理想分布区间，从而精确求出补偿量，即当胶合镜1、透镜5 和透镜7 的单边偏心小于0.01 mm 以及透镜10 单边偏心小于0.008 mm，胶合镜1 倾斜小于45′′，透镜2 倾斜小于 60′′、透镜5 倾斜小于 50′′，透镜7 倾斜小于 60′′时，可满足理论设计对彗差的要求，使光学系统MTF 达到指标要求。

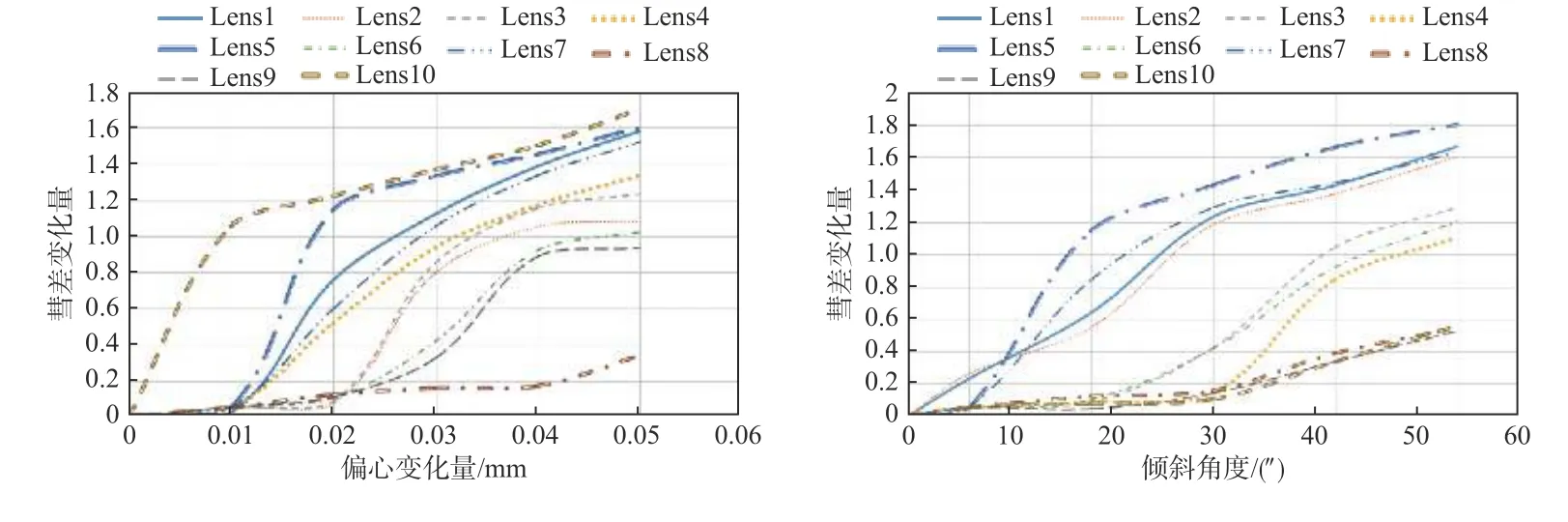
图3 偏心与倾斜彗差仿真结果Fig.3 Simulation results of eccentricity and tilt coma

表3 光学元件敏感等级Table3 Optical element sensitivity grades

3 光学系统共轴调试

根据中心偏测量仪原理及应用方法[16]，设计了一种共轴调试装置，通过芯轴与主镜筒内孔紧配合，完成对变焦相机主镜筒机械内孔轴与直线光杆导轨的平行性进行精确测量，保证动组组元光轴的共轴精度，从而降低彗差对光学系统成像质量的影响，测量原理如图4所示。

图4 测量原理Fig.4 Principle of measurement

表4为调整后的变焦光学系统光学元件偏心及倾斜调试后的测量结果。各光学元件偏心及倾斜均满足上文中对变焦系统敏感光学元件的分析结果。表5为变焦光学系统在长短焦极限位置时的MTF 测量值。通过对变焦光学系统中敏感光学元件空间姿态的调整，测得长焦极限位置时轴上MTF 值为0.453，短焦轴上MTF 达到0.552；长焦轴外0.7 视场MTF 为0.256，短焦轴外0.7 视场MTF为0.358，结果满足设计要求。调整后的变焦光学系统长短焦极限位置的彗差分别减小到0.011 λ和0.008 λ。

表4 偏心调试结果Table4 Eccentric adjustment results

表5 长短焦MTF 实测值Table5 Measured value of long and short focal length MTF

4 结论

本文采用CodeV 软件分析了光学元件不同空间姿态变化时的像差特点，在此基础上确定了影响光学系统成像质量的敏感光学元件，并针对性地完成了调整。除此之外，采用了一种同轴调试装置，对变焦相机主镜筒机械内孔轴与直线光杆导轨的平行性进行了精确测量，保证了动组组元光轴的同轴精度，实现了变焦光学系统各组元偏心的快速调试。最终检测结果表明，在变焦光学系统装调过程中采用该方法，可降低装调过程中彗差的影响，使传递函数MTF 满足设计要求。