圆柱型层析计算全息技术研究

鲁文超，易 青，周 皓，吴 丹,，杨俊义，顾济华

（1.苏州大学 光电科学与工程学院，江苏 苏州 215006；2.苏州大学 文正学院，江苏 苏州 215104）

引言

全息技术是目前三维显示中最受关注的技术之一。计算全息技术能对软件构成的虚拟三维物体进行显示，具有便于存储、不限光波段等优点，在三维显示研究领域受到越来越多的关注。一般的计算全息通过计算三维物体的平面全息图，仅能获得单个视角再现像[1-6]。若要实现多视角观察，需要生成不同角度的计算全息图，增加了计算复杂度。为了消除水平方向的视角限制，有学者提出采用圆柱型计算全息实现 360◦显示。该方法将物面与全息面视为同心圆柱面，通过计算物面到达全息面的衍射光场，并引入虚拟参考光以获得干涉图样。

许多学者们对计算圆柱全息技术进行研究，得到了一系列极具参考价值的实验结果：2005年，Sando 等人通过定义物体和全息图为同心圆柱面来满足位移不变性，在空域中通过卷积方法计算圆柱全息图，模拟过程用了3 次快速傅里叶变换（fast fourier transform,FFT），比直接计算方法快10 000倍[7]；2013年，Sando 课题组又提出了基于三维傅里叶频谱的圆柱全息图快速计算方法，通过三维物体与它在三维傅里叶空间衍射波前的关系来计算圆柱面的衍射光波进而生成圆柱全息图，过程中使用一维卷积运算和一维反傅里叶变换实现快速计算[8]；2007年，Sakamoto 等人提出平面层析方法将三维物体分成若干切面，得到平面物光波，并利用平面与圆柱面旋转平移不变性生成圆柱全息图，能再现三维物体120°视角内的信息，但无法再现深度信息，且实验生成13 mm×13 mm×13 mm大小物体的全息图需要2.76 小时[9]；2010年，Jackin等人定义物体和全息图为同心圆柱面，将Hankel变换应用到计算圆柱全息图生成过程中，只用了2 次FFT 计算[10]；2013年，Jackin 等人利用球谐函数生成了球面物体的球面全息图并进行再现[11]；2015年，Zhao Yu 等人在三维物体与圆柱全息面之间加入波前记录面，利用FFT 计算波前记录面进而生成圆柱全息图，提高了运算速度[12]；圆柱全息技术中一般都采用由内向外传播的模型，2017年，Wang Jun 等人提出了由外向内传播模型，推导了对应的衍射方程，并再现圆柱面物体证实了方法的有效性[13]；2019年，Anton Goncharsky 等人提出了在圆柱表面计算和合成衍射光学元件（diffractive optical element,DOE）的方法，获取的计算全息图以相位反射DOE 形式保存下来，当白光照射时就可以 360◦显示三维图像[14]；2019年，Chang Chenliang等人将彩色物体圆柱面的R、G和B 三色分量分为3 个不同的圆柱面进行计算，叠加后得到彩色物体的圆柱全息图，实现了彩色物体的显示[15]。但是，上述的计算圆柱全息方法采用的是单层圆柱面物体，并没有研究拥有不同景深三维物体的360◦显示，因此有必要对一般性三维物体的计算圆柱全息生成与再现进行研究。

文中研究了一种可对任意三维物体进行360°观察的圆柱型层析计算全息技术：将三维物体分成若干个圆柱面，每层圆柱面均包含物体部分信息，分别计算所有圆柱截面在全息面上的衍射光场，叠加后与参考光干涉获得三维物体的计算圆柱全息图，对所得全息图再现即可实现三维物体的360°不同深度的观察。在确定圆柱全息图半径和高度的情况下，研究了物体圆柱截面半径和波长变化引起空间频率和传递函数的变化，并结合实验分析再现图像质量。采用对应三维地球模型作为原始物光波开展实验，计算圆柱全息图并进行再现以验证方法有效性。

1 原理

1.1 圆柱型层析计算全息

一般的计算全息得到的平面全息图只能从某一个视角来观察再现物体。为了能够对物体进行360°观察，设定全息面为圆柱型，物面为全息面的同心圆柱面，这样可以保证系统的位移不变性，以便利用FFT 进行快速计算。将三维物体分成多层圆柱面，物体所在的每层圆柱面与全息面位置关系如图1（a）所示，其顶视图如图1（b）所示。

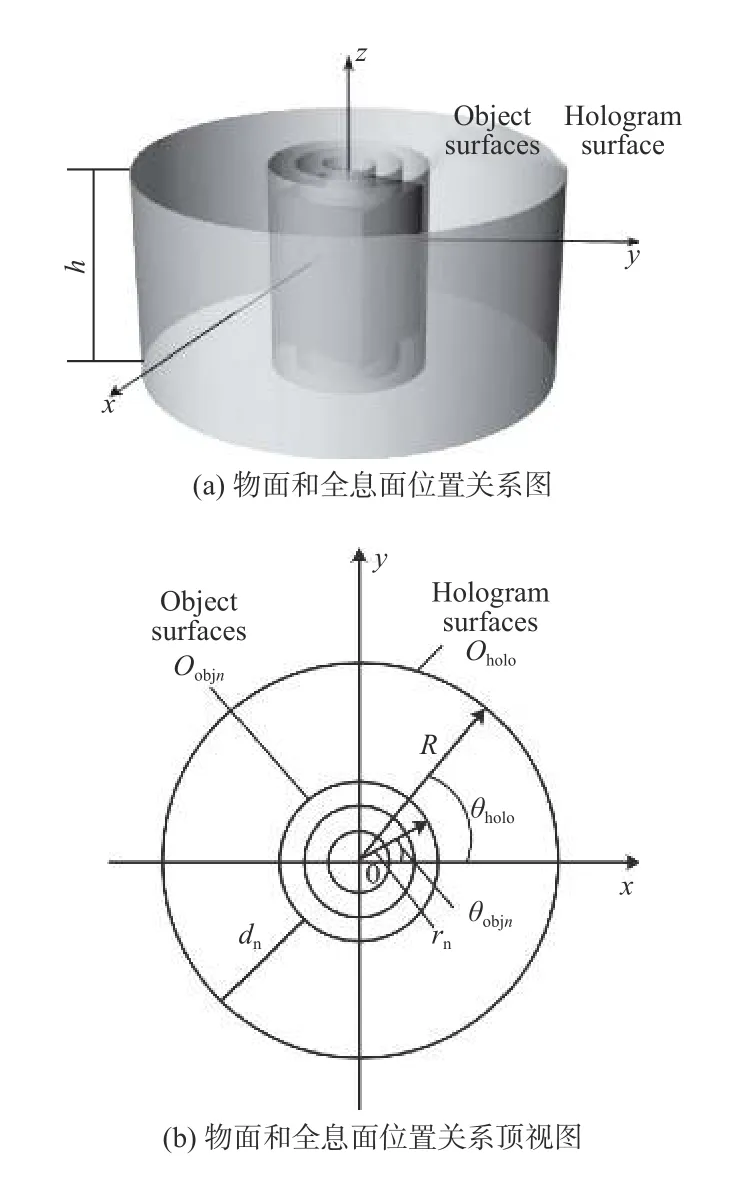
图1 物面和全息面位置关系Fig.1 Relations between object surfaces and holographic surfaces

假设三维物体第n层圆柱截面的光波分布表示为Oobjn(θobjn,zobjn)，全息面的光场分布表示为Oholo(θholo,zholo)。 半径为rn的物面上每一点光波传播到半径为R的全息面上，两点之间传播距离为：

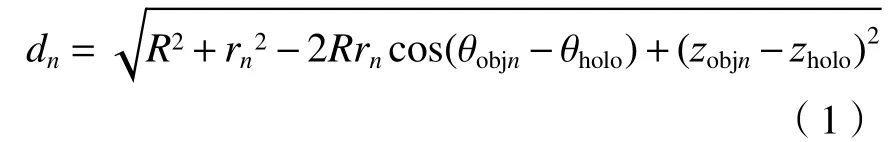
点扩展函数可表示为

若三维物体总共分为N层圆柱面，则全息面的光场分布可表示为

式中：k为波数，，λ 为波长，∗表示卷积运算。由（2）、（3）式可知：不同半径物体圆柱截面对应不同的点扩展函数，物光波与点扩展函数卷积之后叠加得到物体传播到全息面的光场。

全息面光场与参考光干涉得到三维物体的计算圆柱全息图H：

式中：ℜ为参考光；conj表示共轭。

1.2 空间频率与采样间隔

为了更好地重建图像，必须使圆柱方位角 θ和高度z方向上同时满足采样定理的条件。本文先通过点扩展函数二阶偏导数获得函数的极值点，然后分析2 个方向上的空间频率获得采样间隔需满足的条件。

在 θ方向对点扩展函数p(θ,z)求二阶偏导数并令其等于0 得到：

图2 PSF 二阶偏导数与θ的关系Fig.2 Relations between second partial derivative of PSF and θ

θ方向的空间频率表示为

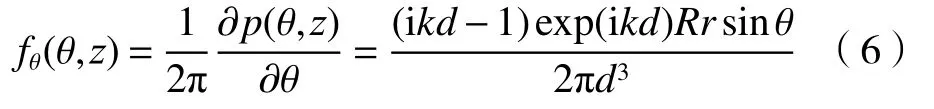
一阶偏导数在 [-π,-π/2)内 递增，在(-π/2,π/2)内递减，在 (π/2,π]内 递减。所以在 sinθ=1或sinθ=-1时 取得最值点。然后计算出 θ方向的采样间隔应满足取模之后得到

在圆柱高度z方 向对点扩展函数p(θ,z)求二阶偏导数并令其等于0 得到：

计算得到 -12π2z4=0，解得z=0 ，由于z≠0时，所以一阶偏导数递减。圆柱高度z方向的空间频率表示为

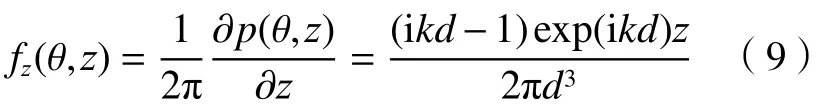
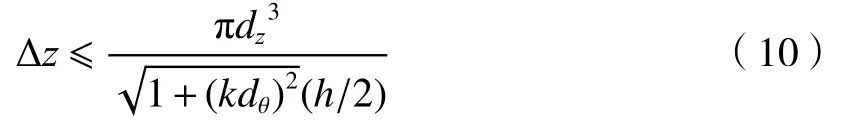
2 实验

2.1 再现像质量分析

为了评价圆柱型层析计算全息系统的成像能力，依据（6）式和（9）式，空间频率由点扩展函数一阶偏导数求得，对点扩展函数做傅里叶变换便得到系统传递函数。通过分析物体圆柱面和波长的变化对点扩展函数一阶偏导数和传递函数的影响来分析再现像质量，并通过仿真实验来进行验证。物面和全息面高度为10 cm，圆柱全息面半径为10 cm，波长为300 μm，r取值范围为0～0.2 m，sinθ=1 时，PSF 在 θ方向一阶偏导数极值点变化情况如图3（a）和图3（b）所示；物面和全息面高度和圆柱全息面半径条件不变，r= 0.01 m 时，λ取值范围为300 μm～1 100 μm，z=h/2时，PSF 在z方向一阶偏导数极值点变化情况如图3（c）和图3（d）所示。

图3 PSF 在θ方向和 z方向一阶偏导数变化情况Fig.3 Changes of first partial derivative of PSF in θand zdirections

对点扩展函数进行傅里叶变换得到系统传递函数，图4（a）～图4（c）分别是波长为300 μm，物圆柱面半径为10 mm、5 mm 和2 mm 时的传递函数。图4（d）～图4（f）分别是物圆柱面半径为10 mm，波长为400 μm、500 μm 和600 μm 时的传递函数。

通过以上对点扩展函数一阶偏导数和传递函数的分析可知，当全息面半径、物面和全息面高度确定，在满足采样定理条件下，物体圆柱面半径越趋近于全息面半径，或者波长越小时，空间频率越大，传递函数分布范围越大，成像质量也就越好。

本文采用一张512×512 像素大小的圆柱面物体开展实验来验证以上分析，物面如图5所示。

图4 不同条件下的传递函数Fig.4 Transfer functions under different conditions

图5 物体圆柱面Fig.5 Cylindrical surface of object

设定物面和全息面高度为10 cm，全息面半径为10 cm，波长为300 μm 时，物圆柱面半径分别为2 mm、4 mm、6 mm、8 mm 和10 mm 时再现情况如图6所示，表1为再现像与原图像的峰值信噪比和均方误差。

对波长改变的情况进行实验研究，设定物面和全息面高度为10 cm，全息面半径为10 cm，物体圆柱面半径设为1 cm，波长分别为300 μm、350 μm、400 μm、450 μm 和500 μm时再现情况如图7所示。表2为再现像与原图像的峰值信噪比和均方误差。

图6 （a）～（e）分别为物圆柱面半径2 mm、4 mm、6 mm、8 mm和10 mm 时的再现图Fig.6 Reconstructed images while radii of cylindrical cross sections are 2 mm、4 mm、6 mm、8 mm and 10 mm

表1 物圆柱面半径2 mm、4 mm、6 mm、8 mm 和10 mm 时再现像与原图的PSNR 和MSETable1 PSNR and MSE while radii of cylindrical cross sections are 2 mm、4 mm、6 mm、8 mm and 10 mm

图7 （a）～（e）分别为波长300 μm、350 μm、400 μm、450 μm和500 μm 时的再现图Fig.7 Reconstructed images while wavelengths are 300 μm、350 μm、400 μm、450 μm and 500 μm

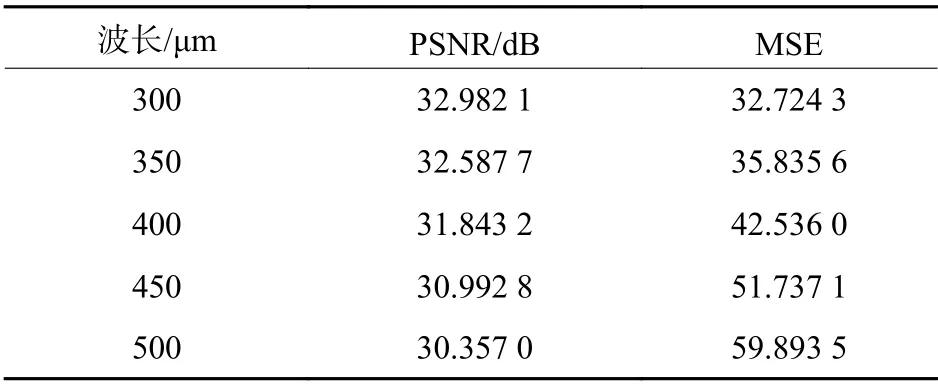
表2 波长300 μm、350 μm、400 μm、450 μm 和500 μm 时再现像与原图的PSNR 和MSETable2 PSNR and MSE while wavelengths are 300 μm、350 μm、400 μm、450 μm and 500 μm

由上述实验结果分析可知：在满足采样定理，确定波长、物面和全息面高度与全息面半径的情况下，随着物体圆柱面半径变大，峰值信噪比也变大，均方误差变小，再现像质量越来越好；在确定物面和全息面高度以及物面与全息面半径的情况下，随着波长变大，峰值信噪比变小，均方误差变大，再现像质量越来越差，验证了本文的再现像质量分析是正确的。在计算三维物体圆柱全息图时，在满足采样定理条件下，选取较大的物面半径和较小的波长有利于得到更清晰的再现像。

2.2 圆柱型层析计算全息实验

文中采用三维地球模型开展圆柱型层析计算全息实验，三维地球模型如图8所示。物体圆柱面与全息面高度均为10 cm，全息面半径设定为10 cm，参考光波长200 μm，分层后的物体圆柱面大小为512×1 024，最大半径为1 cm。采用1.1 节方法计算圆柱全息图，并再现不同角度和深度的信息。

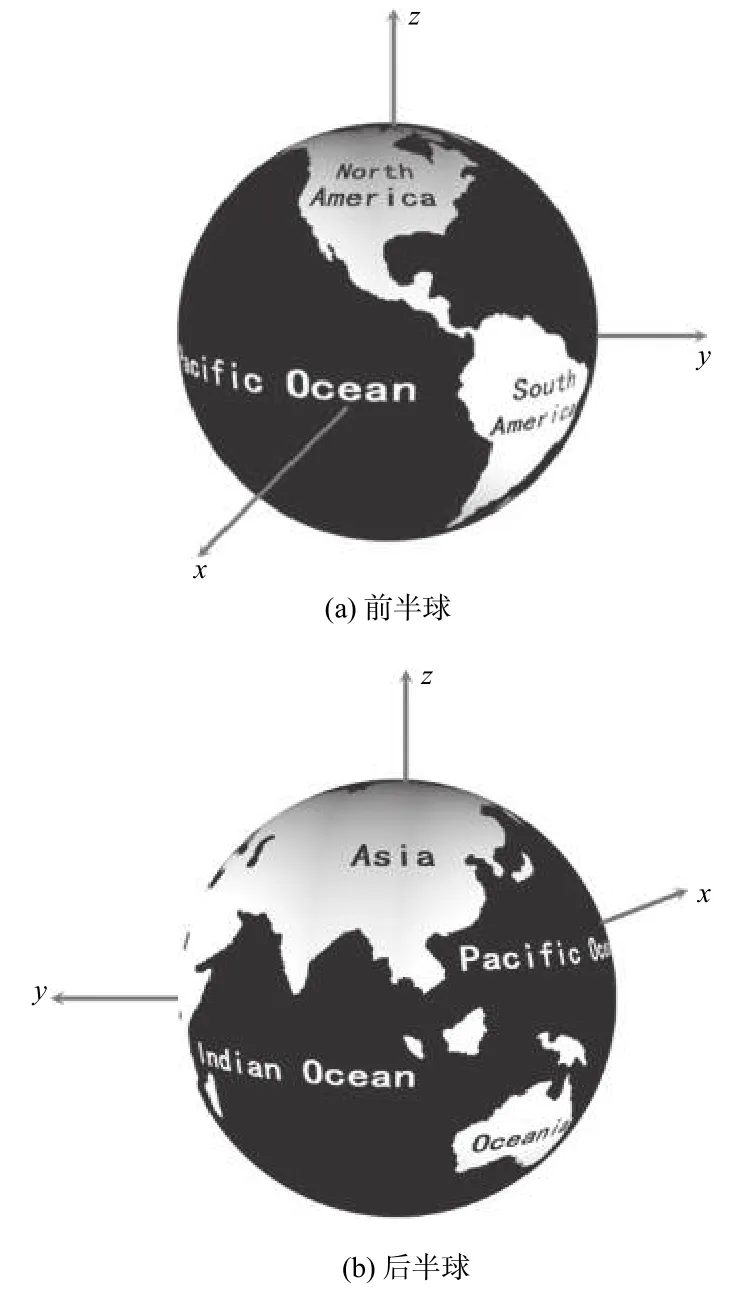
图8 三维地球模型Fig.8 Three-dimensional earth model

2.3 仿真实验结果

按上述实验过程计算得到了地球模型在半径为10 cm 的圆柱全息面上的全息图，大约用时2.5 s，如图9（a）所示。之后采用圆柱面再现和平面再现两种方法对再现结果来进行观测，圆柱面再现方法如下：

式中oc表示第n层的圆柱面再现像。再现柱面半径为1 cm 时圆柱面再现图如图9（b）所示。此时虚线框中的区域聚焦，其他区域均处于离焦状态。

图9 计算圆柱全息图和圆柱面再现图Fig.9 Computer generated cylindrical hologram and cylindrical surface reconstructed image

平面再现方法如图10 所示。再现平面高度为10 cm，宽度为2 cm。因为再现平面和全息面不是同心圆柱面，不满足位移不变性，所以通过直接积分计算再现像：

式中：op表示平面再现方法的再现像；U×V为物体圆柱面像素大小；ruv表示全息面上与再现平面上对应的点的距离。

图10 计算圆柱全息图平面再现示意图Fig.10 Schematic diagram of planar reconstruction for computer generated cylindrical hologram

再现结果如图11 所示，图11（a）与图11（b）选取的再现角度范围相同，均为[-5π/18,13π/18]，但是再现平面深度不同。图11（a）中再现平面位于r= 10 mm 处，正好等于三维地球模型的半径，所以在中心处虚线框内的“uth”清晰，其他区域离焦；图11（b）中再现平面位于r=9.6 mm处，小于地球模型半径，虚线框中聚焦位置也随之改变，距离中心不远处的 “S”和“ca”清晰；图11（c）选取的再现角度范围为[-π/2,π/2]，再现平面位于为r=10 mm处，在中心处虚线框内的“an”清晰，其他区域离焦；图11（d）选取的再现角度范围为[0,π]，再现平面位于r=9.4 mm处。虚线框中聚焦位置相比（b）离中心更远，“Afr”清晰。

图11 （a）～（d）平面再现图Fig.11 Planar reconstructed images

本实验采用圆柱面再现以及平面再现方法2 种方法，对三维地球模型的不同角度和深度的信息进行了再现观测，结果验证了文中方法实现了三维物体圆柱全息图的生成以及不同角度和深度的再现。

3 结论

文中研究了一种圆柱型层析计算全息技术：将三维物体各分层圆柱截面光波与对应的点扩展函数卷积后叠加得到全息面物光波分布，与参考光干涉后生成计算圆柱全息图。分析了物体圆柱面半径、波长变化对空间频率和系统传递函数的影响，采用峰值信噪比和均方误差对再现图像质量进行评价。在此理论基础上确定实验参数，有利于获得更加清晰的三维物体不同角度和深度的再现像。以三维地球模型作为实验对象生成圆柱全息图并进行再现，得到了较好的三维物体的不同角度与深度的再现结果。实验结果表明，本文的方法对三维物体的 360◦全视场显示具有较高的应用价值。