汽车主减速器齿轮间隙对整车振动特性的影响

刘兵 吕岩 王玉磊

（中汽研汽车检验中心（天津）有限公司）

在我国汽车工业高速发展的今天，对于汽车传动机构要求硬件产品具有高精度与高可靠性。然而在汽车的设计、加工以及装配过程中，机构间的间隙是不可避免的。间隙处运动副构件之间的碰撞和冲击会使接触碰撞力增大，加剧接触表面的破坏，导致间隙进一步扩大，引起整车系统的噪声与振动，对机构的动力学特性产生不利影响[1]。为了深入研究间隙对于汽车主减速器齿轮转子系统动力学特性的影响，文章提出了考虑多间隙耦合的汽车主减速器齿轮机构动力学模型，通过开展动力学验证试验研究，并结合试验数据，对比分析汽车主减速器齿轮转子系统的动力学特性。

1 多间隙齿轮机构系统动力学模型

汽车减速器主要依靠齿轮机构进行运动的传递，其中存在很多直齿轮机构，由于直齿轮机构在加工及装配中存在一定的误差，因此减速器齿轮传动系统必然存在齿侧间隙与齿轮的径向间隙[2]。为了研究间隙对减速器齿轮传动系统的振动影响，建立考虑多间隙的汽车减速器齿轮机构非线性动力学模型，如图1 所示。

图1 汽车减速器齿轮机构动力学模型

1.1 多间隙耦合模型

径向间隙（cri/mm）可用图1 中矢量ebrg表示：

最大嵌入量（δimax/mm）为：

在汽车减速器齿轮工作过程中，将会产生径向碰撞，造成汽车减速器齿轮转子系统的径向跳动，导致齿侧间隙大小时刻变化。在图1 中，epg表示实际中心距（AR/mm）：

从式（3）可以看出，AR与间隙矢量密切相关，AR的变化会进一步导致齿侧间隙的改变。根据汽车减速器齿轮转子系统的结构特点，齿轮之间的实际啮合位置会使实际中心距发生明显的变化，时刻变化的齿侧间隙（bt/mm）可表示为：

式中：A0——齿轮初始中心距，mm；

α0——齿轮的初始啮合角，（°）；

b0——齿轮的初始齿侧间隙，mm；

Rp'——主动轮的分度圆半径，mm；

sg'——从动轮节圆齿厚，mm；

Zp——主动轮的齿数；

sp'——主动轮节圆齿厚，mm；

ebrp——主动齿轮间隙矢量；

α'——主、从动轮齿啮合时的实际啮合角，（°）。

根据式（1）、式（3）、式（4），得出动态齿侧间隙（bt/mm）的函数表达式为：

1.2 径向碰撞力模型与齿轮啮合力模型

利用L-N 模型[3]建立齿轮轴承在某一接触点处的径向碰撞力模型，其表达式为：

式中：Fr——主、从动轮的轴承碰撞力，N；

Kr——接触刚度系数；

n——力指数；

Rj——轴半径，mm；

Rb——轴套半径，mm；

δ——嵌入量，mm；

Cr——阻尼系数；

υb，Eb——轴套的泊松比和弹性模量；

υj，Ej——轴的泊松比和弹性模量；

ce——恢复系数；

m——阻尼力指数；

主、从动齿轮之间的动态啮合力（Ft/mm）可表示为：

其中：

式中：Kt——时变啮合刚度，表示主减速器齿轮转子系统啮合数变化对啮合刚度的影响；

Ct——非线性阻尼系数；

fg——间隙关系函数；

gt——啮合过程中的位移函数；

km——平均啮合刚度；

ka——刚度幅值；

ωm——啮合频率，是与齿数和转速相关的函数；

φ——初始相位；

R'p，R'g——调整后的主、从动轮半径，mm；

ebrpx，ebrpy——矢量 ebrp在 x、y 方向的分量；

ebrgx，ebrgy——矢量 ebrg在 x、y 方向的分量。

利用间隙函数描述主、从动齿轮之间的相对啮合关系。即：

从式（13）可以得出，汽车减速器齿轮转子系统中的相对啮合关系即为：当gt（t）≥0 时，正常啮合；当bt（t）＜gt（t）＜0 时，处于脱齿状态；当gt（t）≤-bt（t）时，出现齿背碰撞。

式（10）中的啮合阻尼力的主要参数为非线性阻尼系数Ct，用于描述能量损失，即：

式中：Cm——最大阻尼系数；

d——最大嵌入量，mm；

β——嵌入比。

1.3 齿轮系统动力学模型

根据汽车减速器齿轮转子系统的特点得到它的动力学模型，即：

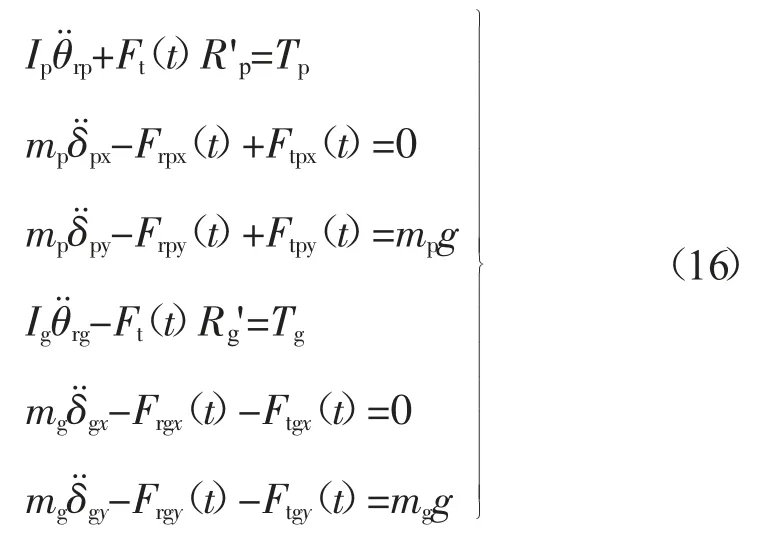
mp，mg——主、从动齿轮的质量，kg；

Tp——驱动力矩，N·m；

Tg——负载力矩，N·m；

Frpx（t），Frpy（t）——主动齿轮轴承碰撞力在坐标系中 x、y 轴上的分量；

Frgx（t），Frgy（t）——从动齿轮轴承碰撞力在坐标系中 x、y 轴上的分量；

Ftpx（t），Ftpy（t）——主动齿轮啮合力在坐标系中x、y 轴上的分量；

Ftgx（t），Ftgy（t）——从动齿轮啮合力在坐标系中x、y 轴上的分量；

g——重力加速度，m/s2。

当水平放置时，g=0。

2 减速器系统振动特性分析

目前国产减速器存在噪声大、振动大、寿命短等问题[4]，针对这些问题，利用上述动力学模型探讨间隙对汽车减速器振动特性的影响。

首先根据实际情况在齿轮箱中安装直齿轮传动部分，探究在直齿轮传动过程中，直齿轮间隙的存在对汽车减速器振动的影响。

为了研究不同速度对汽车主减速器系统响应的影响，选择直流伺服电机作为测试装置，可调速度范围为800～2 200 r/min。为了避免电动机本身的振动对试验数据产生影响，将电动机和底座分开安装，动力通过同步带传递。三轴加速度传感器用于测量沿中心线方向的加速度，此方向不仅可以观察到轴和齿轮接触和碰撞时的振动频率，而且可以观察到该方向齿轮啮合振动的分量。加速度传感器通过信号收集器将收集的加速度信号发送到工控机。测试系统的特点是可以轻松调节齿轮径向间隙的大小和轴承的间隙，同时可以控制驱动速度，然后研究齿轮转子系统在多种情况下的振动特性。测试平台中使用的设备的主要参数，如表1所示。

表1 主减速器系统振动特性测试设备参数

齿轮的具体结构参数，如表2 所示。

表2 汽车减速器齿轮转子系统结构参数

根据表1 和表2 的参数，进行相应的数值计算和试验，将数值计算结果与试验结果进行比对。试验主要测量从动齿轮轴的振动加速度，因此在数值计算中也同样获取该项计算数据与试验数据进行比对。

对于传动系的扭转振动情况，通过在试验与仿真中测得飞轮旋转副、变速箱输入轴轴承、变速箱输出轴轴承和主减速器输入轴轴承的相对转速，处理得到扭转振动角位移综合幅值，将测试值与仿真值进行对比，如图2～图5 所示。

图2 汽车传动系统飞轮端振动响应

图3 汽车变速箱输入端振动响应

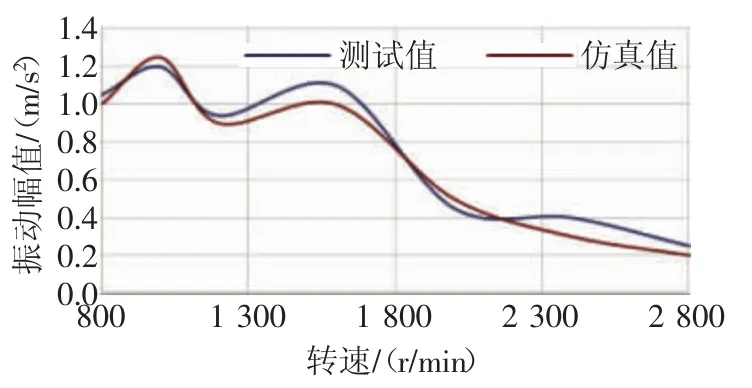
图4 汽车变速箱输出端振动响应

图5 汽车变速箱侧面外壳振动响应

从图2～图4 可以看出，在飞轮端、变速箱输入端及输出端，仿真数据的变化规律与试验数据的变化规律基本一致，而在变速箱侧面外壳的振动响应存在较大误差，如图5 所示。初步分析误差的原因为变速箱外壳结构对系统振动的响应存在一定的增强作用。在汽车主减速器飞轮端出现的最大振幅明显高于其它测试位置，而之后峰值便一直衰减，没有再发生共振现象。

从图3 可以看出，在汽车变速器的输入端转速为900 r/min 时，该位置的振动峰值最大。随着转速的增加，振幅会快速衰减，当转速处于1 600～2 400 r/min 时会出现振动的波峰。通过分析可知，在这2 个转速下，齿轮由于多间隙耦合的现象，发生了共振。对比试验数据与仿真数据可以发现，汽车齿轮多间隙耦合模型的数值计算结果与变速箱试验振动数据的误差较小，并且能够准确地预测出该位置的2 次共振现象。从图4可以看出，在变速箱的输出端发生了1 次共振，之后振幅随着转速的增加快速衰减，最后逐渐平缓。

3 结论

文章提出了一种考虑多间隙耦合的汽车主减速器齿轮系统动力学模型，在模型中考虑了多种间隙之间的相互耦合等非线性因素，并且对该汽车主减速器齿轮系统动力学模型进行试验验证。通过分析试验结果发现：

1）在飞轮端、变速箱输入端及输出端，仿真数据的变化规律与试验数据的变化规律基本一致，而在变速箱侧面外壳的振动响应存在较大误差。

2）误差源主要为：在数值计算中，通过理论公式得到的接触刚度和阻尼的数值与装置的实际情况存在一定误差；其次，受驱动轮轴和轴套加工精度的限制，表面粗糙度与理论模型之间存在差异，导致出现误差；最后，由于有齿加工误差的影响，实际齿侧间隙会偏离理论值且分布不均匀，导致出现误差。

3）汽车主减速器齿轮系统由于多间隙耦合的现象，发生了共振。对比试验数据与仿真数据可以发现，汽车齿轮多间隙耦合模型的数值计算结果与变速箱试验振动数据的误差较小，并且能够准确地预测出共振现象。

4）在未来的研究中，要选用高精度齿轮和轴套进行试验。