基于迭代学习控制的双容水箱液位控制

侯君虹

（陆军步兵学院 石家庄校区，石家庄 050000）

0 引言

在现代工业生产控制过程中，主要的被控量通常为：液位、流量、温度和压力4 种。其中，液位作为这4 种常见被控量中最容易测量和直接观察的被控量，理所应当受到的关注也是最多[1]。而双容水箱作为最常见的液位控制对象，工业上很多复杂的被控对象常常抽象为它的数学模型来研究。所以，对双容水箱的液位控制研究具有很广泛的应用背景和很重要的研究价值。

可是双容水箱系统一般呈非线性，并且存在着容积延迟，液位变化缓慢，系统惯性比较大等问题[2]。实践证明，传统PID 系统对双容水箱的调节时间比较长且控制效果并不是很好。

迭 代 学 习 控 制（Iterative Learning Control，ILC）由Uchiyama 于1978 年首先提出[3]，影响较小，后来Arimoto等[4]又于1984 年用英文发表。该方法的基本策略是，针对一类在有限区间上重复运行的非线性动态系统，通过前一次或前几次运行得到的误差信息和控制输入信息来修正当前的控制输入信息，以便可以使得整个重复任务可以取得更好的效果，如此不断重复，知道在整个时间区间上，系统的输出完全跟踪期望轨迹[5,6]。

本文为双容水箱的液位控制提供了一种利用I/O 数据的控制方式——ILC。首先对ILC 进行了详细的研究，然后利用控制系统的I/O 数据得到一次迭代的控制量，进而对双容水箱的液位进行控制，最后在MATLAB 中进行仿真，得到多次迭代后的仿真图，通过这些仿真图可以看出ILC的有效性。

1 迭代学习控制

考虑如下连续被控系统：

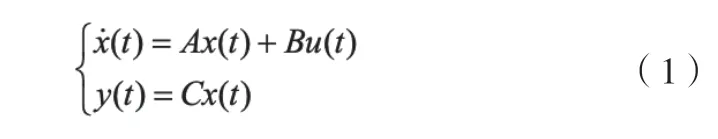
其中，x∈Rn，u∈Rr，y∈Rm，x为系统的状态向量，u为系统的控制向量，y为系统的输出向量。假设系统在时间区间[0,T]不断重复，最终使得y(t)→yd(t)。

在第k 次运行时，式（1）表示为：

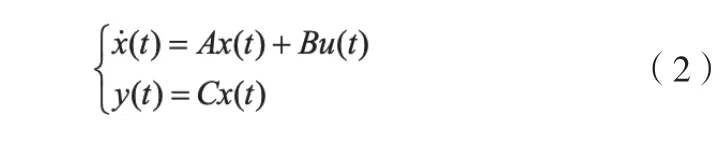
输出误差为：

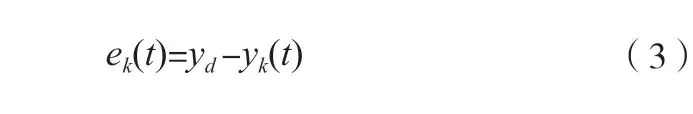
迭代学习控制的目标：对给定的控制对象，在规定的时间t∈[0,T]，寻找优化的控制输入uk(t)，使得当迭代次数k 趋于无穷时，系统的输出信号yk(t)与期望轨迹yd(t)之间的偏差为零[7,8]。

关于目前已有的迭代学习控制的学习律包括P 型、D 型、PID 型、高阶学习算法以及带遗忘因子的学习算法[9-11]，本文将详细介绍PID 型学习律。

PID 型学习律可以描述为：

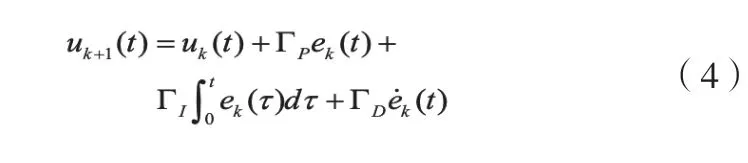
由于PID 型学习律算法简单有效、计算量小，且需要极少的系统先验知识，从而得到了广泛和深入的研究，是最成熟的迭代学习控制算法之一[12]。

闭环迭代学习控制的迭代效果要好于开环迭代学习控制，因为在迭代的过程，它使用的是本次操作时的输出误差，而不是上一次迭代的输出误差。开环迭代学习控制采用的是离线的计算方法，对系统的计算要求不高；闭环迭代学习控制存在部分在线计算量，对系统的要求更高。

每一次迭代结束时，需要检验是否满足停止条件。若满足，则停止运行。设ε 为设定的允许跟踪精度，一般的停止条件为：

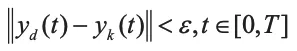
迭代学习控制算法具体算法流程[8]如下所述，设t∈[0,T]：

1）k=0 时，给定期望输出yd(t)，初始输入u0(t)。

2）对被控对象施加输入uk(t)，采集并存储yk(t)。

3）计算输出误差ek(t)=yd-yk(t)，根据迭代学习律，计算出下一次控制输入量，存入存储器中。

4）检验停止条件，若满足，停止迭代；若不满足，则k=k+1，跳入第二步重复运行。

2 控制器参数优化方法

开环PID 型迭代学习控制器参数优化的过程是基于对迭代过程收敛性分析得出的[13,14]。

设被控对象为线性时不变的离散系统，其传递函数为：

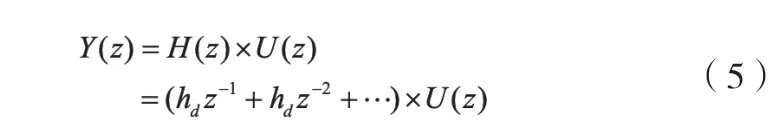
其中，z-1为标准的时间延迟算子，参数hi为系统H(z)的标准Markov 参数。并且该系统在时间[0,T]上不断重复运行，k 表示迭代次数。定义下列向量：

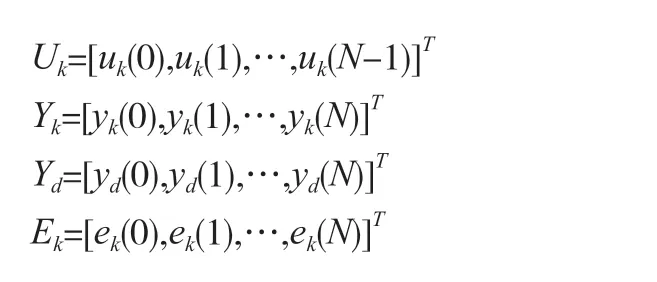
则受控系统（6）可以表示为：

则Hp为由被控对象Markov 参数构成的矩阵为：

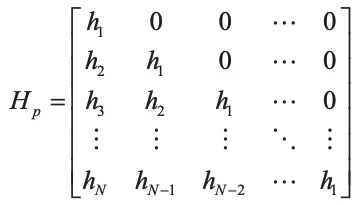
则受控系统的离散PID 型迭代学习控制律为：

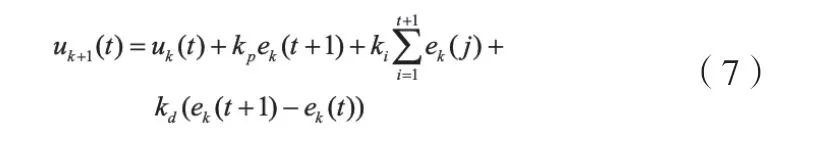
其中，kp，ki， kd为PID 型迭代学习控制器的参数。

式（6）采用向量的形式为：

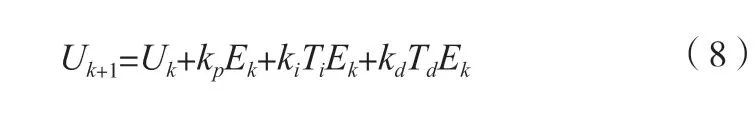
其中，Ti=T([1,1,…,1]T)，Td=T([1,-1,…,0]T)。

由（6）式可得：

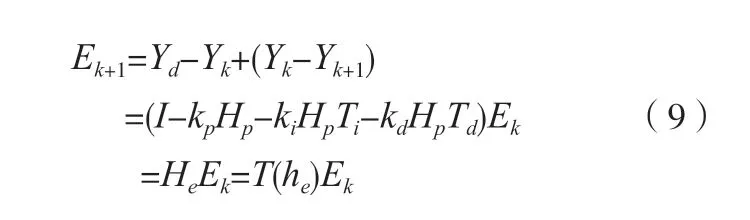
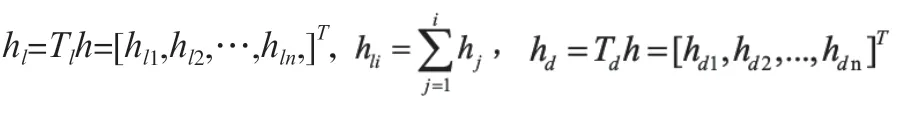
经计算可以得到：

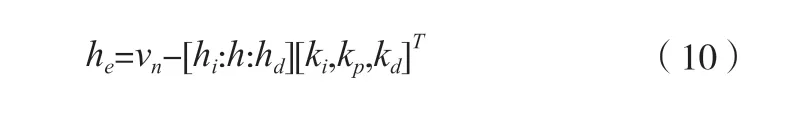
整个迭代过程的收敛条件为：

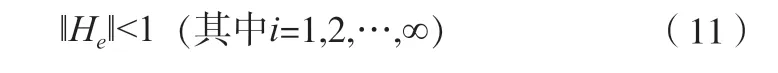
由于He是一个下三角的Toelitz 矩阵，可知：

且有He=T(he)，所以条件ǁHeǁ＜1 是Ek的1-范数和∞-范数收敛的充分条件，这样ILC 参数的设计就会转换成求解合适的kp，ki，kd使得ǁHeǁ＜1。从而，使得应用简单的数学计算方法来完成ILC 参数的设计成为可能。

定义下面优化设计的性能指标：

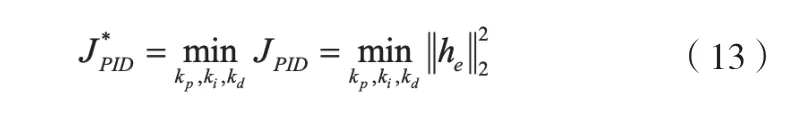
令H=[hi:h:hd]∈RN×3和gPID=[kp,ki,kd]T，并对g 求导，经过一系列计算可得：

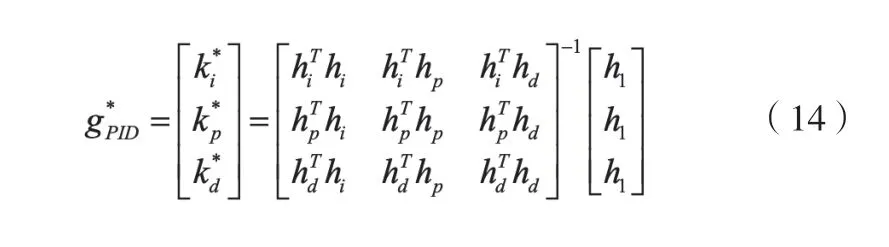
式（14）就是求得学习控制器最优参数，采用此数据结果可以缓解收敛速度慢的问题，加快学习收敛速度。

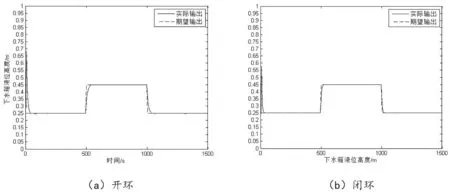
图1 输出跟踪曲线Fig.1 Output tracking curve

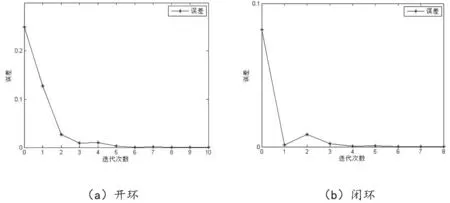
图2 误差变化图Fig.2 Error variation chart

关于连续系统迭代学习控制器参数优化的方法可以借鉴离散系统的求法，但条件是连续系统必须保证在整个仿真过程中采样时间（仿真步长）不变。

3 仿真

通过对双容水箱进行机理建模[2]，可以得出其传递函数为：

其中，A1=A2=2m2，R1=0.3656，R2=0.305[15]。

根据开环 PID 型迭代学习控制器参数优化的方法可以得出：Kp=1.4005，Ki=0.0084，Kd=12.5495。

另外，通过实验试凑法得出闭环PID 型迭代学习控制器参数如下：Kp=4.5，Ki=1，Kd=20。可以得出迭代学习控制的输出跟踪曲线和误差变化曲线分别如图1、图2 所示。

具体部分数据见表1。

从图1 的（a）（b）可以看出，开环PID 型迭代学习和闭环PID 型迭代学习都可以实现对双容水箱的控制。从图2 和表1 可以看出闭环迭代学习控制只需要较少迭代次数便可以实现精确地跟踪，这是因为开环迭代学习控制只利用了系统的前一次信息，而闭环迭代学习在系统前一次信息的基础上更好地利用了系统的当前信息。但是，由于闭环迭代学习控制系统学习律参数是通过实验试凑得到的，过程往往复杂却得不到理想的控制效果。在本文中闭环迭代学习控制系统对双容水箱的跟踪速度更快。

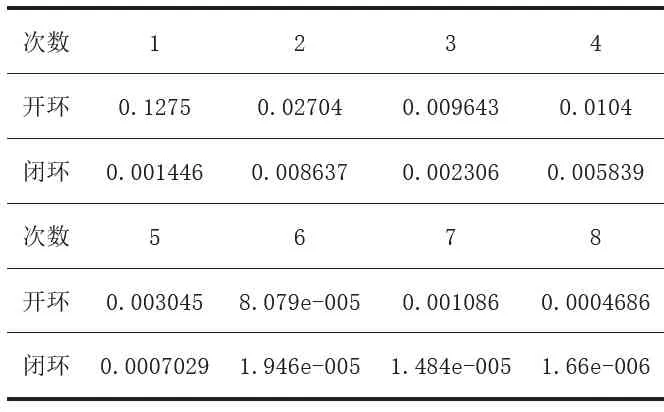
表1 误差eTable 1 Error e

4 结束语

将迭代学习算法应用于双容水箱的液位控制中，通过仿真结果表明：不管是开环PID 型迭代学习还是闭环迭代学习都可以取得较好的控制效果，达到了较高精度的跟踪控制要求。在本文中对开环PID 型迭代学习的学习律参数进行了优化设计，使其参数可以通过简单的数学计算得到，不需要进行反复的试凑，这也是开环迭代学习优于闭环迭代学习的地方。因此，对闭环迭代学习的学习律参数需要做进一步的研究，得出一个更加便捷的方法。