基于有向图的评分改进算法设计与实现

陈佳伊，李红波，崔伟灿，王 吉，应正波

（浙江中控技术股份有限公司，杭州 310053）

0 引言

一所现代化工厂成功的一个重要因素就是具有较高技术水平和丰富经验的现场操作人员。传统的师傅带徒弟的一对一培训模式由于效率低下，已经逐渐被淘汰，采用虚拟控制仿真培训系统不仅可以大大提高培训效果，节省培训费用，缩短培训时间，而且可以降低装置操作的不确定性，减少或避免事故发生。同时仿真培训可以培养一人多岗，一专多能的高素质人才，为企业的长期发展提供人才保障，是国内外公认的煤化工、石油化工等领域最高效的现代化技能培训与考核手段。

目前OTS 仿真培训的评分算法采用的是单向链表的数据结构，评分规则单一，对评分配置的限制诸多，难以满足工程上对于评分规则灵活性的要求。本文提出了一种评分关系依赖模型，改进了评分规则算法，使得工程实施时的灵活度和便利性大大提高。

1 建立评分关系依赖模型

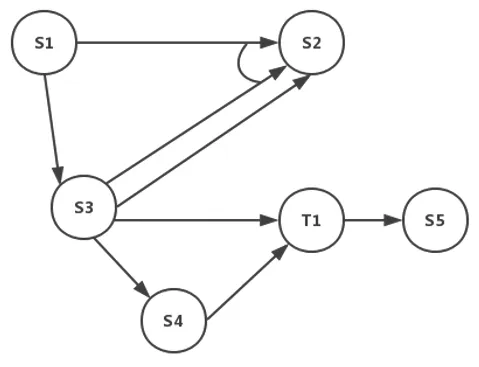
图1 有向图表示步骤间依赖关系示例图Fig.1 An example diagram of a directed graph of inter-step dependencies

在培训过程中，教员使用评分组态软件设计一套评分规则对学员的现场操作进行考察，构成评分规则的基本元素为评分步骤。步骤表示操作员的一个操作动作，不同步骤根据不同的规则组合在一起，用于评定操作员的操作顺序是否正确，操作是否达到预期目标。

一个步骤可以抽象为有向图中的一个节点，在此将步骤记为S。步骤与步骤之间存在依赖关系，依赖关系的类型有时间关系、顺序关系和引用关系。时间关系用于考察两个关联的步骤是否在设定的时间关系内完成，顺序关系考察两个关联的步骤是否按照设定的次序被执行，引用关系表示一个步骤引用另一个步骤的状态作为该步骤的评分依据。例如，步骤2 引用步骤1 的完成状态作为该步骤开始的条件。

步骤的最终计算结果与步骤间的依赖关系有关，步骤的时间关联和顺序关联也可抽象为有向图中的一个节点，分别记为T 和O，引用关系和函数关系以箭头方式表示。在评分关系依赖模型中存在多个依赖关系确定步骤状态的情况，记为{O,T-＞S}，其中O,T-＞S 的含义即为顺序依赖关系O 和时间依赖关系T 共同确定步骤S 的状态。图1 表示了这种依赖关系，其中用圆弧连接两条有向边表示节点间存在“与”的关系，“或”关系未在图中做出特殊标记。

2 评分算法的设计与实现

2.1 构建最小函数依赖集

步骤的规则属性间存在函数依赖关系，该函数依赖关系反映了规则属性间的关联性和数据的完整性约束。而由于各步骤规则属性间存在错综复杂的依赖关系，为了使依赖关系简单、明了，减少在实际运算过程中的重复运算，首先需要求解模型的最小函数依赖[1]集以简化运算。在求解最小函数依赖集的过程中，传统的算法能解决相应问题，但不够直观，将有向图的表达运用到函数依赖关系中去，会使得问题的求解更加清晰、直观。

下面给出最小函数依赖集F'的求解算法：

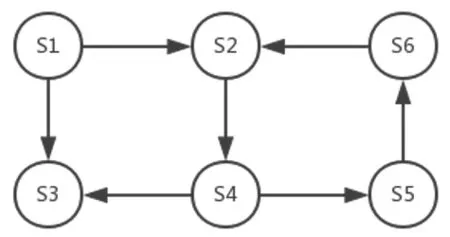
图2 深度遍历模型示例图Fig.2 Depth traversing model sample

1）根据函数依赖集F，画出步骤间依赖关系的有向图，其中各节点表示各个步骤或时间、顺序关系、引用关系，有向边表示函数关系，有向边箭头的起始结点为决定因子。

2）考察图中每条边，如果出现平行边，则删除存在“与”的关系的那组边，由于在函数依赖集中不会出现完全相同的函数依赖关系，所以这里的平行边只会存在于一条独立边与一组“与”边中的其中一条。

3）如果图中某个结点到达另一个节点的路径有多条，则删除直接相连的边，保留经过其他节点到达的边。经过简化后，消除了由传递函数依赖导致的多余函数依赖。

4）将变换后的图中属性间的关系转换为函数依赖关系的表达，得到的函数依赖集即为最小函数依赖集F'。

2.2 环的存在与检测

得到步骤关系依赖图，在对步骤进行拓扑排序前，需要对步骤间的依赖关系进行环路检测，保证得到的步骤关系依赖图是一个有向无环图[2]。如果存在环路，步骤间接引用自身的状态将会导致死循环。例如，步骤1 引用步骤3 的考试结束状态作为步骤开始的条件，步骤3 引用步骤2的考试结束状态作为步骤开始的条件，步骤2 又引用步骤1 的考试结束状态作为步骤开始的条件，此时步骤1 又去获取步骤3 的考试状态，造成死循环。

这里采用着色法检测有向图中是否存在环路，检测算法如下：

1）分别对每个节点进行深度遍历。

2）对每个节点的状态进行标记，白色代表此节点还没有被处理；灰色代表此节点正在被处理，或者说他的儿孙们还没有被处理；黑色代表此节点以及其所有儿孙都已经被处理过了。

3）在深度遍历时，如果到达了一个灰色的节点，说明该有向图中存在环路。

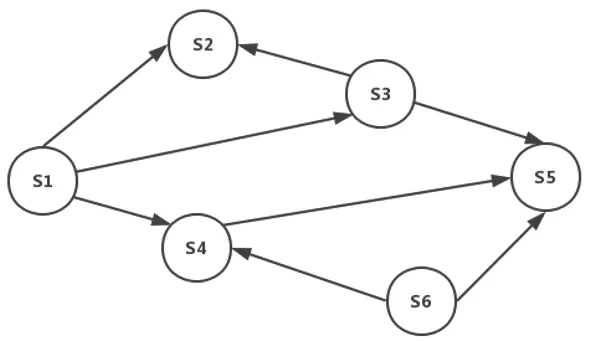
图3 评分关系模型示例图Fig.3 An example of scoring relationship model

以图2 为例，以深度优先搜索S1 节点时，先将S1 标记为灰色，依次寻找子节点得到S1-＞S3，到达S3 节点时发现不存在子节点，将S3 标记为黑色。继续搜索得到S1-＞S2-＞S4-＞S3,到达S3 节点时发现不存在子节点，将S1、S2 标记为黑色，此时对S1 节点搜索完毕，继续搜索S2 节点，先将S2 标记为灰色，依次寻找子节点得到S2-＞S4-＞S5-＞S6-＞S2，此时S2 的状态为灰色，该图中存在环路。

2.3 建立拓扑序列图

以下面的评分关系模型为例，如图3 所示。

在未经排序优化前，步骤根据默认的顺序进行计算，过程如下：

1）计算得到S1 的评分结果。

2）对S2 进行评分计算-＞获取本轮评分中S1 和上一轮评分中S3 的结果-＞得到S2 的结果。

3）对S3 进行评分计算-＞获取本轮评分中S1 的结果-＞得到S3 的结果。

4）对S4 进行评分计算-＞获取本轮评分中S1 和上一轮评分中S6 的结果-＞得到S4 的结果。

5）对S5 进行评分计算-＞获取本轮评分中S3 和上一轮评分中S4、S6 的结果-＞得到S5 的结果。

6）对S6 进行评分计算-＞获取本轮评分中S4、S5 的结果-＞得到S5 的结果。

由此可见，采用默认的计算顺序会导致评分计算轮次混杂，步骤的依赖数据未更新，甚至出现引用同一个步骤得到的计算结果不一致的问题，而实际应用中的模型远比上述模型复杂的多，更容易出现难以预料的结果。建立拓扑序列图[3]，对评分中的最小元素进行计算顺序的排序可以规避这种问题，拓扑排序算法如下：

① 在步骤关系依赖图中选一个没有前驱节点的节点并且输出。

② 从图中删除该节点和所有以它为尾的边。

③ 重复上述两步，直至所有节点输出，或者当前图中不存在无前驱节点的节点为止，最后得到整理好的拓扑序列。

以图2 的关系模型为例，展示拓扑排序过程：

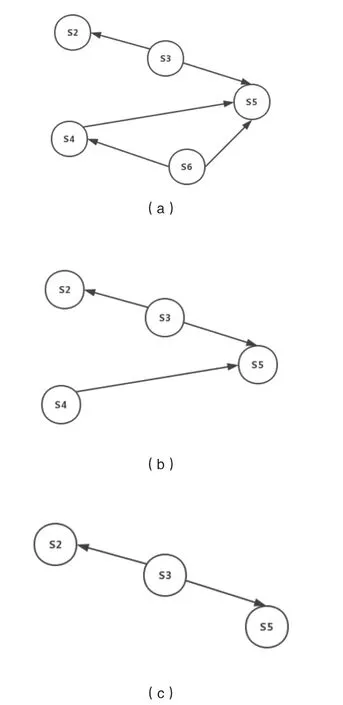
图4 变换后的步骤关系图Fig.4 Transformed step diagram

首先，发现S6 和S1 没有前驱节点，随机选择一个输出，这里选择先输出S1，删除和S1 有关的边，得到如图4(a)所示结果。

然后，继续寻找没有前驱节点的节点，发现S6 没有前驱节点，输出S6，删除和S6 有关的边，得到如图4（b）的结果。

然后，又发现S4 和S3 都是没有前驱节点的，这里选择先输出S4，得到如图4（c）结果。

然后，继续输出没有前驱节点的S3，此时只剩下两个没有前驱节点的节点S2 和S5，输出S2 和S5。最后全部节点输出完成，整理得到该图的一个拓扑序列为：S1-＞S6-＞S4-＞S3-＞S2-＞S5。

此时按照拓扑顺序依次计算步骤状态，可以保证步骤引用的每个依赖数据都是本轮次的最新数据。

3 结论

本文提出了一种基于有向图的工业仿真培训系统评分关系依赖模型，解决了在评分计算中的步骤状态循环引用检测问题，提高了评分规则设置的灵活性。同时对原有的评分算法进行了改进，提出了一种计算顺序重排算法，解决了在同一轮次中计算结果不一致的问题，规避了风险。