优越扩张下的投射性
汪 杰,周 珺,赵志兵
安徽大学 数学科学学院,合肥 230601
0 引言
广义倾斜模(也称Wakamastu倾斜模)首先由Wakamastu[1]提出并研究的,后成为倾斜理论和同调代数理论的重要研究对象.一方面,广义倾斜模本身具有很好的性质,更重要的是广义倾斜猜想,即具有有限內射维数的广义倾斜模是余倾斜模或等价的,一个具有有限投射维数的广义倾斜模是倾斜模,这一猜想与很多重要的同调猜想联系在一起.例如可利用著名的有限维猜想,推出广义倾斜猜想,进而可利用广义倾斜猜想,推出对称猜想和广义猜想[2-4].本文中的R,S均指带有单位元的交换环,R-模均指酉模.
定义1.1 设RW是一个有限生成的左R-模,若称RW为一个广义倾斜模(或称为Wakamastu倾斜模)[2],如果满足下列条件:
(1)对于每个i≥1,ExtRi(RW,RW)=0;
(2)存在正合列
使得每个Ti∈addRW(i≥0),这里的addRW指的是由所有的同构于RW的有限直和的直和项构成的左R-模的全子模范畴,且用HomR(-,RW)作用后上述正合列仍是正合的.

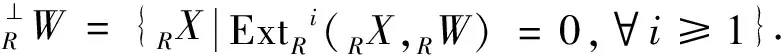
作为Gorenstein投射模[11]的推广的形式,Bennis和Quaighi[5]定义了X-Gorenstein投射模类,这里的X指的是包含投射模类的一个模类并统一了一些重要的模类.事实上,若令X为所有的模类,则X-Gorenstein投射模即为经典的投射模,若令X为投射模类,则X-Gorenstein投射模即为经典的Gorenstein投射模.

P:…→P1→P0→P0→P1→…

注2:根据文献[6]中的结果,本文有:

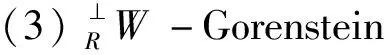
优越扩张是一类重要而有意义的环扩张,经典的例子包括域上的群代数是这个群的具有有限指数的正规子群代数上的一个优越扩张,一个环上的矩阵是这个环的一个优越扩张等等,见文献[7].在优越扩张下,许多的同调性质和表示性质均是保持的[8].
定义1.3 设R是S的子环且R与S具有相同的单位元,则称S是R的一个环扩张,记为RS.一个环扩张RS称为优越扩张,若满足:
(1)S是R的有限正规扩张,即存在a1,a2…an∈S,使得S=Ra1+Ra2+…+Ran.
(2)S作为R-模是自由的,即有RS≅RR(n).
(3)S是R-投射的,即若SM是SN的子模,当RM|RN时必有SM|SN,这里M|N是指M是N的直和项.

1 主要结果
命题2.1 如果RW是一个广义倾斜R-模,RS是一个优越扩张,则SS⊗RW是一个广义倾斜模.
证明:显然有SS⊗RW是有限生成的,这是因为SR是一个有限生成的自由模.对任意的i≥1,有:
ExtSi(SS⊗RW,SS⊗RW)≅ExtRi(RW,HomS(SR,S⊗RW))
≅ExtRi(RW,RS⊗RW)≅ExtRi(RW,RW(n))由于对任意的i≥1,ExtRi(RW,RW)=0,从而ExtRi(RW,RW(n))=0;于是对任意的i≥1,有:ExtSi(SS⊗RW,SS⊗RW)=0.
另一方面,因为RW是一个广义倾斜R-模,于是存在正合列:
T:0→RR→T0→T1→…→Ti→…
其中Ti∈addRW(i≥),且用HomR(-,RW)作用上述正合列仍正合.现用张量积SS⊗R-作用得到:
SS⊗RT:0→SS⊗RR≅S→SS⊗RT1→SS⊗RT2→…→SS⊗RTi→…
其中,SS⊗RTi∈addSS⊗RW(i≥1),从而有:
HomS(SS⊗RT,SS⊗RW)≅HomR(T,HomS(SSMSS⊗RW))≅HomR(T,RS⊗RW)≅HomR(T,RW)⊗RS
第一个同构是由连接同构得到,第二个同构是由张量赋值同构得到.由于HomR(T,RW)是正合的,且RS是自由的,所以HomS(SS⊗RT,SS⊗RW)是正合的.
综上所述,SS⊗RW是一个广义倾斜模.

命题2.2 设RS是一个环的优越扩张,RW是一个广义倾斜R-模且模X是一S-模,当且仅
ExtSi(SS⊗RX,SS⊗RW)≅ExtRi(RX,HomS(SR,SS⊗RW))≅ExtRi(RX,RS⊗RW)≅ExtRi(RX,RW(0))
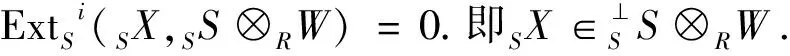

0=ExtSi(SS⊗RX,SS⊗RW)≅ExtRi(RX,HomS(SR,SS⊗RW))≅ExtRi(RX,RS⊗RW)


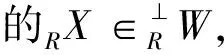
命题2.4 设RS是一个的优越扩张,RW是一个广义倾斜R-模.若RM是一个投射模[11],则SS⊗RM是一个投射模.

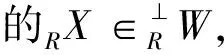
ExtSi(SS⊗RM,SS⊗RY)≅ExtRi(RM,HomS(SS,SS⊗RY))≅ExtRi(RM,RS⊗RY)≅ExtRi(RM,RY(n))=0
这是因为对于任意的i≥1,有ExtRi(RM,RY)=0,又因为有RS≅RR(n),所以可得到式:ExtSi(SS⊗RM,SY(n))=0.于是对任意的i≥1,有ExtSi(SS⊗RM,SY)=0;
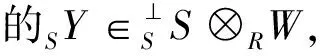
HomS(SS⊗RP,SY)≅HomR(P,HomS(SS,SY))≅HomR(P,RY)
所以HomS(SS⊗RP,SY)是正合的.
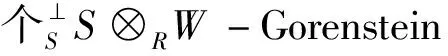
命题2.5 设RS是一个环的优越扩张[12],RW是一个广义倾斜R-模.M是一个S-模,则有RM是一个投射模当且仅当SM是一个投射模.
证明:“⟹”:根据命题2.4,以及X-Gorenstein投射模类保直和项的性质易知显然成立.

ExtRi(RS⊗SM,RS⊗RX)≅ExtSi(SM,HomR(RS,RS⊗RX))≅ExtSi(SM,SS⊗RX)
ExtSi(SS⊗RX,SS⊗RW)≅ExtRi(RX,HomS(SS,SS⊗RW))≅ExtRi(RX,RS⊗RW)≅ExtRi(RX,RW(0))=0

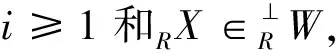
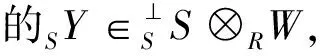
HomR(RS⊗SP,RX)≅HomS(P,HomR(RS,RX))≅HomS(P,SS⊗RX)


