水平荷载作用下轴压比对框架—泡沫混凝土复合墙板影响的有限元分析
钱 坤,董沛雨,丁芳芳
吉林建筑大学 土木工程学院,长春 130118
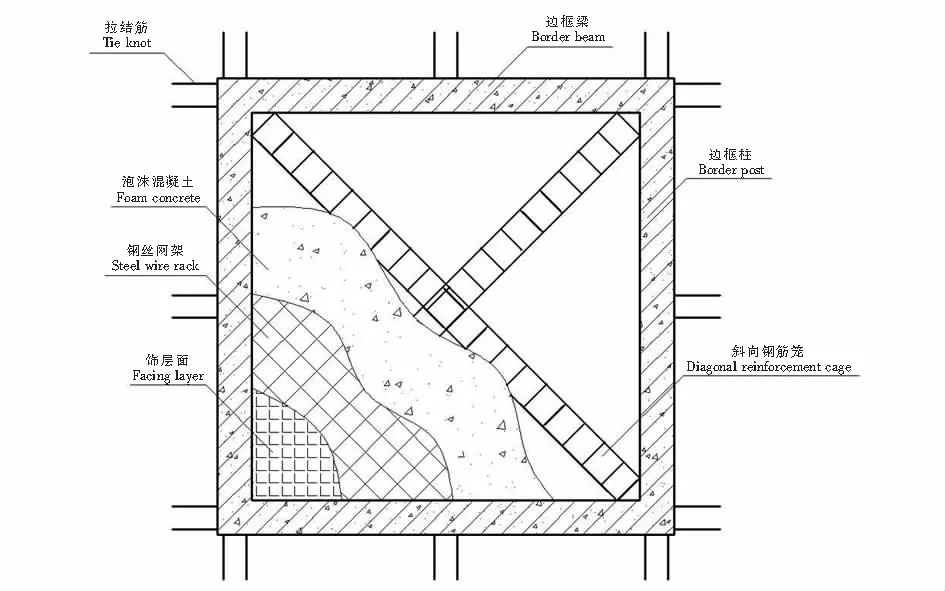
图1 复合板构造
框架—泡沫混凝土复合墙板具备轻质、抗震、环保的优点,是一种新型构造形式,如图1所示.一方面,墙板中斜向肋条约束钢筋和钢筋肋条间的发泡混凝土砌块,使其共同承担荷载,同时各肋条构成斜向钢筋笼,受到砌体的反向约束;另一方面,隐形框架和墙板构成统一整体,形成相互作用的复合墙体.在国内外墙板的抗震性能研究中,构件的轴压比、剪跨比和水平配筋等是重要研究内容,其中对于墙板在不同轴压比下受力状态和抗震性能的研究较多[1-4],如对不同轴压比的框架—泡沫混凝土复合墙板进行了试验研究,并取得了一系列成果,但由于复合墙板结构新颖,受力状态复杂,并不能单纯依靠模型试验.
本文利用ABAQUS有限元软件进一步分析了轴压比对框架—泡沫混凝土复合墙板的影响,通过建立8组水平和竖向荷载共同作用下的框架—泡沫混凝土复合墙板模型(复合墙板的轴压比分别取0.1,0.2,0.3,0.4,0.5,0.6,0.7,编号为BW 2~BW 8;取轴压比为0的一组为参照组,编号为BW 1;泡沫混凝土密度为1 000 kg/m3)进行数值模拟分析,得到不同轴压比下复合墙板的受力状态和抗震性能.
1 有限元模型的建立
1.1 分析模型
复合墙板的设计尺寸为1 500 mm×1 600 mm×100 mm,各构件截面尺寸及配筋情况如图2所示.有限元模型尺寸与复合板设计尺寸取11,混凝土等级采用C 30.

(a)试件尺寸(a)Section of specimen (b)1-1 (c)2-2 (d)3-3
1.2 本构关系
利用ABAQUS有限元软件对复合墙板进行分析时,首先要确定各构件材料的本构关系,即应力-应变关系[5-6].
1.2.1 混凝土的本构关系
本文参考《混凝土结构设计规范》(GB 50010-2010)[7]中附录C中的公式,来确定混凝土的本构关系.
受压区本构方程:
当x≤1时
y=αa+(3-2αa)x2+(αa-2)x3
(1)
当x≥1时
(2)
(3)
(4)
式中,αa为曲线上升阶段参数值,αa=2.4-0.012 5fc*;αd为曲线下降段参数值,αd=0.157(fc*)0.785-0.905;ε为混凝土压应变;εc为混凝土峰值压应变;σ为混凝土压应力,MPa;fc*为混凝土轴心抗压强度设计值,N/mm2.
受拉区本构方程:
当x≤1时,
y=1.2x-0.2x6
(5)
当x≥1时,
(6)
(7)
(8)
式中,αt为单轴受拉应力-应变曲线参数值,αt=0.312(ft*)2;ε为混凝土拉应变;εt为混凝土峰值拉应变,εt=(ft*)×65×10-6;σ为混凝土拉应力,MPa;ft*为混凝土轴心抗拉强度设计值,N/mm2.
混凝土力学性质如表1所示.

表1 混凝土模型参数
1.2.2 泡沫混凝土的本构关系
泡沫混凝土应力-应变关系本构方程为:
σ=σ0[2ε/ε-1.1(ε/ε0)2-1.7(ε/ε0)3+3.8(ε/ε0)4-2(ε/ε0)5]
0<ε≤ε0
(9)
σ=σ0[5.2+3.7(ε/ε0)]/[1+7.9(ε/ε0)]
ε0≤ε≤εu
(10)
其他参数如下:
σ0=0,85fck,ε0=0.003,εu=0.006
式中,σ为泡沫混凝土压应力,MPa;σ0为泡沫混凝土压应变为ε0时的压应力,MPa;ε为泡沫混凝土压应变;ε0为泡沫混凝土压应力达到fc时的压应变;εu为正截面泡沫混凝土极限压应变;fck为泡沫混凝土单轴抗压强度标准值,N/mm2.
1.2.3 钢筋的本构关系
为计算简便,钢筋的本构关系采用理想弹塑性模型[8].
σ=E·ε
(11)
式中,σ为钢筋拉应力,MPa;ε为钢筋拉应变;E为钢筋弹性模量,MPa.
1.3 有限元模型
框架—泡沫混凝土复合墙板主要由外框架、复合板边框、钢筋、泡沫混凝土构成.在ABAQUS有限元软件中依次完成对各构件材料属性的定义,装配完成后即完成建模.复合板装配模型如图3所示.

图3 框架-泡沫混凝土装配模型
1.4 模型边界条件和荷载的施加
本文忽略平面外墙体的位移,故将复合板模型底端设定为固定约束;忽略新旧混凝土、混凝土与泡沫混凝土之间的相对滑移,故将框架与边框、框架与底梁、边框与泡沫混凝土墙板之间设置为绑定连接;钢筋设定为内置区域.
为模拟正常工作状态下的框架—泡沫混凝土复合墙板,故在框架梁顶端施加竖向荷载,并根据轴压比的计算公式改变压应力大小,从而达到控制参数变量轴压比大小的效果;在水平方向上,建立作用点RP并将其与加载点处的混凝土面进行耦合,便于施加水平单调位移荷载.
2 有限元结果的分析
2.1 水平荷载作用下不同轴压比复合墙板的受力状态分析
为探寻水平荷载作用下轴压比对复合墙板应力、应变的影响,此处取BW 2和BW 4两块复合墙板进行对比分析,两个模型在单调水平位移荷载作用下的应力和应变见图4~图9.
由图4~图9可清晰地看出,两块复合墙板中各构件分担水平荷载的情况:两组复合墙板应力大小分布情况相似,斜向钢筋笼均承担了大部分的水平荷载;复合边框对钢筋笼构成约束,也承担了少部分荷载,由此体现了斜向钢筋笼与复合墙板边框协同工作的良好机理[9].
总体来说,不同轴压比的复合墙板受到水平荷载作用时,复合墙板受力状态相似,说明在水平荷载作用下轴压比对复合墙板的受力状态无明显影响.
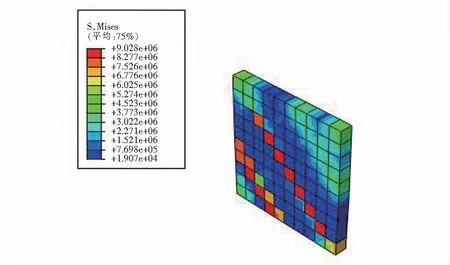
图4 BW 2填充墙应力云图

图5 BW 2整体应力云图

图6 BW 4填充墙应力云图

图7 BW 4整体应力云图

图8 BW 2钢筋笼应力云图
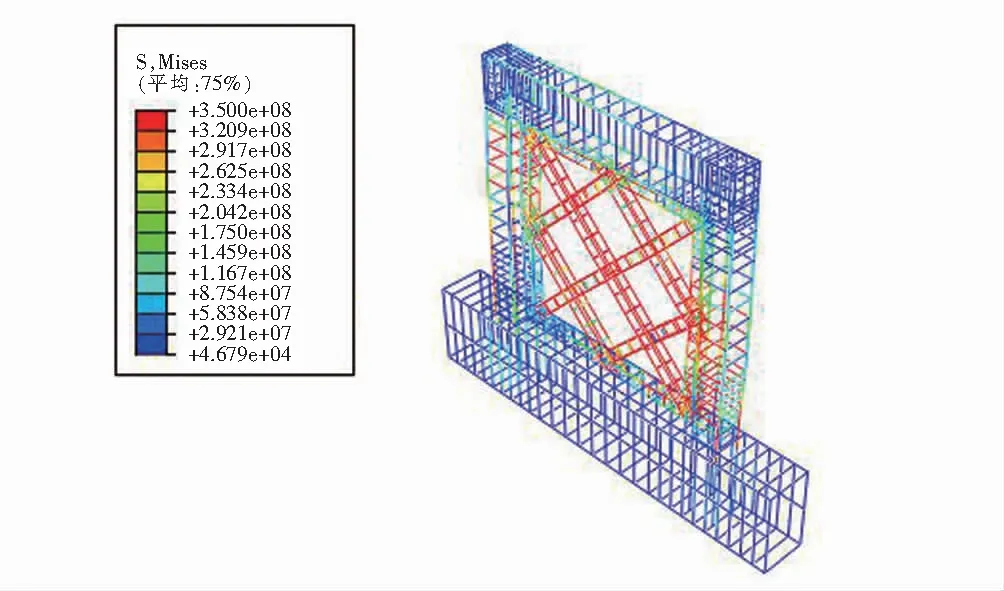
图9 BW 4钢筋笼应力云图
2.2 水平荷载作用下不同轴压比复合墙板的抗震性能分析
2.2.1 骨架曲线
对BW1~BW8模型的应力、应变和变形云图进行整理,绘制出的骨架曲线如图10所示.
由图10 可见,当轴压比小于0.3时复合板承载力增幅明显,承载力与轴压比成正比;当轴压比大于0.3时复合板承载力增幅明显降低.在此次模拟中,随着轴压比的增大,延缓了复合板的裂缝开展,从而裂缝间钢筋的拉应力减小,故承载力提高.当轴压比增大到一定程度,混凝土受压区应力增大,从而抑制了承载力的提高,故承载力增幅明显下降.当轴压比为0~0.3时,压应力较小,对极限位移基本没有影响;当轴压比为0.4~0.7时,复合板刚度逐渐增大;当轴压比大于0.3后,复合板延性急剧减小.只考虑承载力时,轴压比为0~0.5时,承载力逐步增大,轴压比越大越好;只考虑延性时,轴压比为0~0.3时,延性良好,再增大延性将明显降低.综合考虑复合板承载力和位移延性,轴压比取0.3左右最为合理.

图10 骨架曲线

图11 不同轴压比的复合板荷载曲线
2.2.2 承载能力
选取水平荷载作用下复合墙板各力学性能指标,并对BW 1~BW 8模型的应力、应变和变形云图进行数据整理,结果如表2所示.根据表2数据,整理绘制出荷载曲线如图11所示.

表2 轴压比对复合板力学性能指标
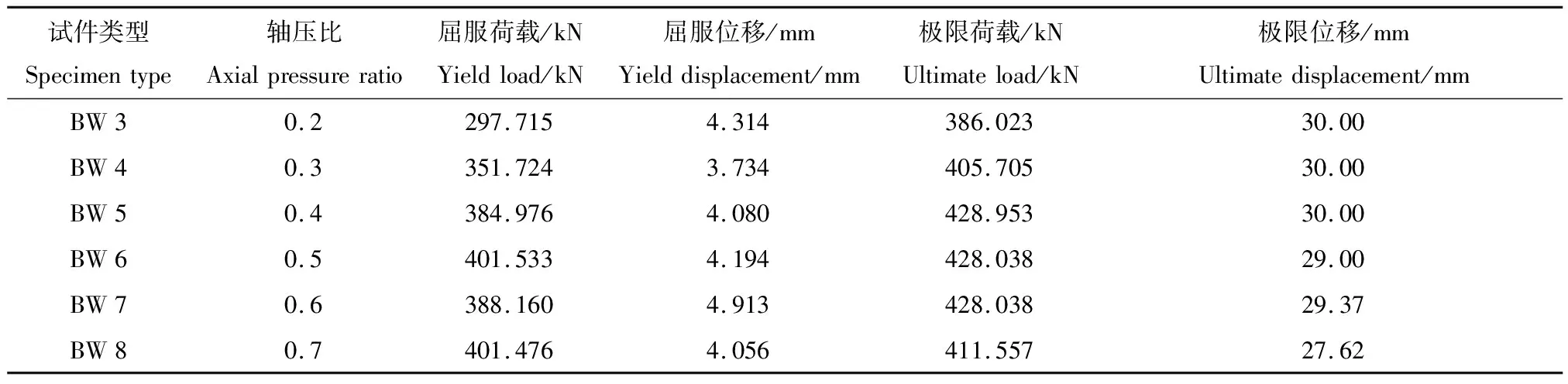
续表2
分析表2和图11可以得出,随着轴压比的增大,复合墙板的屈服荷载和极限荷载也随之增大,但增大趋势有所不同.对于极限荷载,当轴压比小于0.4时,呈直线上升,增幅明显;当轴压比大于0.4时,增幅降低,荷载降低.原因在于,复合墙板截面上产生的压应力与截面受拉一侧的部分拉应力相互抵消,混凝土和钢筋受到的拉应力就会减小,从而极限荷载就会提高.需要注意的是,在混凝土极限压应变不变的情况下,如果增大轴压比,截面受压区高度就会增加,截面曲率延性系数就会降低,所以应该限制轴压比来保证复合墙板的延性.
3 结论
(1)对不同轴压比的框架-泡沫混凝土复合墙板施加水平荷载时,斜向钢筋笼都承担较大荷载,复合边框承担少部分荷载,各构件协同工作.轴压比的变化对复合墙板受力状态无明显影响.
(2)在一定轴压比范围内,复合墙板轴压比越大,承载力越高,但延性越差.当轴压比为0~0.5时,轴压比越大,承载力越大;当轴压比为0~0.3时,延性合适,若超过0.3,延性显著下降.综合考虑,复合墙板的轴压比取0.3左右最为合理.
(3)随着轴压比的增大,复合墙板的屈服荷载和极限荷载随之增大;但在极限压应变不变的情况下,如果盲目增加轴压比将严重影响结构延性,反之应通过限制轴压比来保证复合墙板的延性.

