限制性两阶段多位点全基因组关联分析法在遗传育种中的应用

贺建波，刘方东，王吴彬，邢光南，管荣展，盖钧镒

限制性两阶段多位点全基因组关联分析法在遗传育种中的应用

贺建波，刘方东，王吴彬，邢光南，管荣展，盖钧镒

（南京农业大学大豆研究所/国家大豆改良中心/农业部大豆生物学与遗传育种重点实验室/作物遗传与种质创新国家重点实验室/江苏省现代作物生产协同创新中心，南京 210095）

全基因组关联分析（genome-wide association studies，GWAS）通过建立全基因组高密度分子标记以检测基因型与表型间的关联性，已成为动植物数量性状遗传解析的主要方法。然而，以往GWAS方法只注重于个别主要QTL的检测，而且使用仅有2个等位变异的SNP标记不能检测自然群体中广泛存在的复等位变异，一定程度限制了GWAS的应用。限制性两阶段多位点全基因组关联分析方法（RTM-GWAS）首先根据全基因组高密度SNP标记间的连锁不平衡程度，将多个相邻且紧密连锁的SNP标记组成为具有复等位变异（单倍型）的连锁不平衡区段（SNPLDB）标记。其次，RTM-GWAS使用由SNPLDB标记计算的遗传相似系数矩阵作为群体结构偏差的通用估计，并提取该矩阵的特征向量作为模型协变量以降低由群体结构偏差导致的假阳性。最后，利用具有复等位变异的SNPLDB标记与建立的多位点复等位变异模型，RTM-GWAS将性状遗传率作为QTL表型变异解释率的上限，通过两阶段分析策略高效地进行全基因组QTL及其复等位变异的检测，并最终构建多QTL遗传模型。该法还可以基于性状小区观测值，建立QTL与环境互作多位点模型，不仅能检测与环境有交互作用的主效应QTL，还能检测仅与环境有交互作用的无主效应QTL。RTM-GWAS不仅解决了以往GWAS不能估计复等位变异的问题，而且通过使用多位点模型拟合多个QTL提高了检测功效并能有效地控制假阳性的膨胀，为全面解析自然群体QTL及其复等变异提供了通道。该法能估计出等位基因的效应及其在群体内的相对频率，由其结果建立的QTL-allele矩阵代表了目标性状在群体中的全部遗传组成，不仅可用于候选基因发掘，还为群体内QTL及其复等位变异（基因及其复等位基因）的动态研究（群体遗传分化以及特有与新生等位变异）提供了新的工具。依据QTL-allele矩阵，还能进一步利用计算机模拟产生杂交组合后代基因型，并预测杂交组合后代纯合群体的表现，从而进行优化组合设计与分子设计育种。此外，RTM-GWAS还适用于双亲杂交后代重组自交系群体以及多亲杂交后代巢式关联作图群体，因避免了群体结构偏离的干扰，检测功效更高。本文归纳了RTM-GWAS的原理和方法，并综述了其在遗传育种研究中的应用。

全基因组关联分析；复等位变异；SNPLDB标记；多位点模型；QTL-allele矩阵

作物生产涉及的性状大部分是数量性状，研究和解析数量性状遗传基础不仅对植物遗传研究有意义，而且也是设计育种中组合优化设计和后代精准选择的前提。与质量性状由一个或少数几个基因控制不同，数量性状由大量基因控制，全面准确解析数量性状基因座（quantitative trait locus，QTL）至今仍具有挑战性[1]。目前，基于分子标记的连锁定位（linkage mapping）和全基因组关联分析（genome-wide association study，GWAS）是QTL/基因定位的2种主要方法。连锁定位一般基于双亲分离世代群体，如重组自交系群体（recombinant inbred lines，RIL），利用分子标记遗传连锁图谱和区间作图法进行QTL检测[2-3]。连锁定位通常只涉及2个亲本，该方法所能检测的遗传变异仅限于2个亲本间的遗传差异，例如在RIL群体中，每个遗传位点上最多存在2个等位基因的差异。因此，基于双亲分离世代群体的连锁定位往往只能检测到有限数量的大效应QTL，不能全面检测QTL及其复等位变异。基于多亲分离世代群体的连锁定位方法一定程度上丰富了遗传变异，例如玉米的巢式关联作图（nested association mapping，NAM）群体由25个具有共同亲本的RIL群体组成，则理论上每个遗传位点最多存在26个等位基因的差异[4-5]。然而，以往NAM群体的统计分析方法中将各RIL群体视为彼此独立的子群体，假定每个位点在不同RIL群体中具有不同的等位基因效应[6]，例如由25个RIL群体组成的NAM群体中，每个位点具有恒定的50个等位基因。因此，尽管NAM群体通过一个共同亲本将各RIL群体联系起来，但以往NAM群体的统计分析方法仅仅是多个RIL群体的联合分析，没能将NAM群体作为一个统一完整群体，模型中每个位点的基因型不是真实的分子标记基因型，从而导致每个位点等位基因数目与实际情况有所偏差，进而影响QTL的检测及进一步的育种应用。

自然群体/资源群体具有最广泛的遗传变异。GWAS利用自然群体大量的历史重组事件，通过检测全基因组高密度分子标记与表型的相关性，进而筛选与目标性状显著关联的标记位点，比之连锁定位具有更高的检测精度。GWAS能够检测全基因组QTL及其复等位变异，已经成为数量性状遗传解析的重要方法，广泛应用于人类与动植物数量性状遗传基础解析的研究[7-8]。然而，与连锁定位中群体遗传结构单一不同，自然群体由于长期的自然和人工选择等因素往往具有复杂未知的群体结构，而群体结构又可能导致非连锁位点间产生非随机关联，进而导致GWAS检测结果较高的假阳性[9]。目前，研究者已提出多种方法以降低群体结构对GWAS的干扰，其中最常用的方法主要包括结构关联（structured association，SA）[10]、主成分分析（principal components analysis，PCA）[11]和混合线性模型（mixed linear model，MLM）[12]。SA方法是将由STRUCTURE等[13]贝叶斯聚类算法推断的群体结构作为模型协变量以控制群体结构的影响。与SA方法类似，PCA方法是将群体遗传关系矩阵特征向量作为模型协变量。在SA和PCA的基础上，MLM方法又将遗传背景效应作为随机效应加入线性模型，并将亲属关系矩阵作为遗传背景随机效应的协方差结构，从群体结构和家系结构2个方面控制群体偏差对GWAS的影响。

以往GWAS通常基于全基因组SNP分子标记，而SNP分子标记在一个标记位点上仅有2个等位变异，不能检测自然群体中广泛存在的复等位变异，不仅一定程度限制了GWAS在育种中的应用，由于单个SNP分子标记仅能解析一对等位基因间的遗传变异，因而这也可能降低GWAS的检测功效。上述常用的GWAS方法均基于单位点模型，每个标记位点与表型的相关性测验彼此独立进行，因此，每个标记位点的效应估计会受到相邻位点的影响，从而导致位点表型变异解释率过高估计，例如检测的位点总表型变异解释率可能超过100%。由于GWAS涉及海量的分子标记，这将导致多位点模型中变量个数远大于观测值数目，不能直接求解线性模型，这很大程度上限制了多位点模型在GWAS中的应用。此外，为了控制单位点模型多重测验导致的全试验水平错误率增大，以往GWAS通常使用非常严格的显著水平控制假阳性，例如Bonferroni矫正方法。严格的显著水平同时也将导致较高的假阴性，以至于以往GWAS往往仅能检测到少数主要QTL，检测的位点往往仅能解释表型变异的一小部分，不能全面解析全基因组遗传位点。

针对上述GWAS的局限性，He等[14]将多个相邻且连锁不平衡（linkage disequilibrium，LD）程度高的SNP标记组成具有复等位变异的SNPLDB标记，并基于多位点复等位变异模型进行全基因组QTL检测，提出了限制性两阶段多位点全基因组关联分析方法（restricted two-stage multi-locus genome-wide association analysis，RTM-GWAS），该方法不仅解决了以往GWAS不能估计复等位变异的问题，而且基于多位点模型通过拟合多个QTL，提高检测功效并降低假阳性。RTM-GWAS方法通过全面解析自然群体QTL及其复等基因，建立群体的遗传构成，以进一步应用于基因发掘、群体遗传分化研究以及最优亲本组合的全基因组选择。本文首先总结RTM-GWAS的原理和方法，然后综述其在遗传育种研究中的应用。

1 限制性两阶段全基因组关联分析方法

RTM-GWAS方法包括2个关键创新点以解决以往GWAS不能估计复等位变异和单位点模型的问题。第一点关键创新是基于全基因组高密度SNP分子标记构建具有复等位变异的SNPLDB标记，并利用SNPLDB标记进行QTL检测。SNPLDB标记具有复等位性，因而可以拟合自然群体中丰富的复等位变异。第二点关键创新是建立两阶段多位点复等位变异模型以检测全基因组QTL，并最终构建多QTL遗传模型。多位点模型不仅解决了以往GWAS单位点模型效应估计有偏的问题，而且由于多位点模型不再涉及多重测验问题，从而可以使用常规显著水平，一定程度上能够降低由多重测验矫正导致的假阴性，提高检测功效。

由于GWAS通常涉及海量分子标记，直接求解多位点模型将导致模型空间过大而计算困难。RTM- GWAS方法采用两阶段分析策略以解决GWAS多位点模型计算耗时的问题，第一阶段将大量与目标性状无关的分子标记淘汰，第二阶段基于缩减后的分子标记拟合多位点模型。另外，RTM-GWAS计算程序（https://github.com/njau-sri/rtm-gwas/）基于C++编程语言实现，并借助高度优化的高性能线性代数运算库，使得RTM-GWAS方法具有较高的计算效率[15]。

1.1 复等位变异检测

通常SNP标记在全基因组的分布不是均匀的，相邻SNP间的连锁紧密程度显示出基因组的区段特征，区段内的单倍型序列保持不变的一起传递给下一代。因此，区段内SNP间的连锁不平衡程度较高，区段内多个SNP等位变异的不同组合形式则构成了不同的区段单倍型。区段单倍型提供了类似复等位变异的变异特征，比只有2个等位变异的SNP标记，更符合自然群体基因组变异特征。连锁不平衡是度量自然群体重组历史的通用指标，因此可根据SNP间的连锁不平衡程度在全基因组范围内寻找这种基因组区段。RTM-GWAS首先使用基于连锁不平衡置信区间的方法确定全基因组范围内的基因组区段[16]。按设定的连锁不平衡标准，区段内的SNP可能有多个，最少为一个。这些SNP组成的单倍型类型作为该位点的等位变异，群体内个体在该位点的基因型由这些SNP组成单倍型确定。这种基于连锁不平衡区段构建的具有复等位变异的标记类型就称为SNPLDB标记。

单个SNP同样被视为一个独立的SNPLDB标记。通过比较不同测序深度的数据比较显示，随着SNP密度的增加，仅包含一个SNP的SNPLDB标记将减少。例如，利用145 558个SNP构建获得36 952个SNPLDB标记，其中70.3%的SNPLDB仅包含单个SNP，而基于平均覆盖深度大于11×的数据，78.2%的SNPLDB标记都包含多个SNP[14]。

SNPLDB标记提供了比SNP标记更丰富的复等位变异信息，由于复等位变异是自然群体/资源群体的自然属性，SNPLDB标记理论上能够拟合不同等位基因数目的QTL，基于SNPLDB的QTL检测也比SNP更加合理。SNPLDB标记还可用于分析位点水平不同等位变异在不同亚群中的频率差异，比SNP标记也更适用于群体的遗传分化特征研究。此外，植物常规育种是一个聚合等位基因的遗传操作过程，将亲本材料互补的等位基因聚合到一个复合改良个体中，使其包含产量、品质或其他所需性状的优异等位基因[17]。因此，设计育种的首要前提就是解析目标性状全基因组QTL及其复等位变异组成，而基于SNPLDB的QTL检测为设计育种提供了潜在方法。

1.2 群体结构控制

以往用于群体结构控制的基于分子标记的遗传关系矩阵只适合于SNP标记[11,18-19]，不能用于具有复等位变异的SNPLDB标记。因此，RTM-GWAS利用基于SNPLDB标记的遗传相似系数矩阵以控制群体结构对GWAS的影响。基于SNPLDB标记的个体（假定二倍体）间的遗传相似系数定义为处于状态同样SNPLDB标记的比例，即：

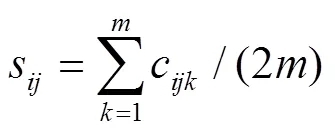
其中，c定义为在第个SNPLDB上个体与个体的共有等位基因数目（取值为0、1、2），是SNPLDB总个数。尽管群体结构由于群体混合或近交程度的变化具有不确定性，但遗传相似系数矩阵无需预先设定假设，可以作为一种通用方法来估计群体结构。RTM-GWAS将遗传相似系数矩阵的特征向量作为协变量纳入线性模型以矫正群体结构偏差。这里，群体结构效应被视为固定效应而不是随机效应，因为群体通常是预先确定的，而不是随机形成的[9]。

1.3 多位点关联分析模型

尽管GWAS通常涉及数百万的分子标记，然而大部分标记与目标性状并不相关。为了有效缩减多位点模型空间，RTM-GWAS采用两阶段分析策略。第一阶段，基于单位点模型进行全基因组位点的关联测验，使用常规显著水平（例如0.05）对标记位点进行初步筛选，淘汰与目标性状不相关的标记位点。线性模型可表示如下：

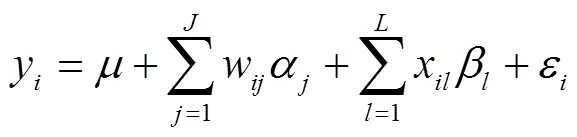
其中，y表示个体的表型观测值；表示总体平均数；w表示遗传相似系数矩阵第个特征向量在个体上的系数，α为第个特征向量的效应，为用于群体结构矫正的特征向量的个数；x为测验标记位点第个等位基因对于个体的基因型指示变量，取值0或1；β为第个等位基因的效应；为测验标记位点的等位基因数目；ε为假定服从正态分布的残差效应。该线性模型可以使用回归分析方法直接求解。

第二阶段，利用如下多位点模型对第一阶段筛选得到的标记位点进行分析，检测全基因组QTL并最终建立多QTL模型。

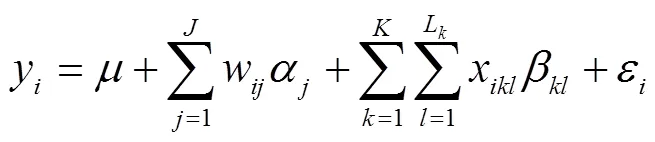
其中，x为第个位点的第个等位基因在个体上的基因型指示变量，取值0或1；β为第个位点的第个等位基因的效应；L为第个位点的等位基因数目；为总QTL数目。其他符号含义同上。该模型可使用逐步回归分析方法进行求解。由于QTL检测基于多位点模型，因此，RTM-GWAS检测的QTL所解释的总遗传变异将小于群体总遗传变异或表型变异解释率不超过性状遗传率。

1.4 全基因组QTL检测显著水平

由于多位点模型内含全试验水平错误控制的特性，因此，RTM-GWAS方法使用常规显著水平0.01和0.05检测全基因组QTL。这与以往基于单位点模型的GWAS方法不同，基于单位点模型的GWAS往往需要按标记一个一个进行大量独立的统计假设测验，即多重测验，此时常规显著水平下的全试验错误率将大大提高。这种情况下，有必要采取适当调整方法对多重测验进行矫正，例如基于Bonferroni方法调整的显著水平0.05×10-8，以控制全试验错误率[20]。但对于RTM-GWAS的多位点模型，所有位点被拟合于一个线性模型中进行联合统计假设测验，因此，使用常规显著水平便可以控制全试验错误率，无需进行多重测验矫正。

根据逐步回归方法的特点，除给出全模型显著的位点外，还可以给出每个入选位点的单独概率或显著性，通常和多重测验的校正概率相近，因而研究者还可根据需要采用特殊标准选取位点。例如，He等[14]使用常规显著水平检测到139个大豆百粒重位点（表1），包括22个大效应（2≥1%）位点和117个小效应（2＜1%）位点，总表型变异解释率分别为61.8%和36.4%。结果还包括了采用Bonferroni方法矫正显著水平检测的16个位点中的15个。因此，尽管没有必要对RTM-GWAS进行多重测验矫正，研究者仍然可以采用更严格的显著水平从常规显著水平下的结果中筛选个别显著程度高的大效应位点，而无需重新计算。例如，对于一个性状改良的育种方案，育种家可以使用0.05或0.01作为显著水平检测QTL，而对于候选基因克隆，研究者可以使用计算给出的单个位点的概率来筛选最重要的基因座位。

表1 中国大豆种质资源群体百粒重显著关联的SNPLDB标记位点

LC QTL：大贡献（2≥1%）QTL；SC QTL：小贡献（2＜1%）QTL。...：省略了部分数据。a：Williams 82第一版参考基因组（Wm82.a1）

LC QTL: large (2≥1%) contribution QTL; SC QTL: small (2＜1%) contribution QTL. “...”: data omitted.a: Williams 82 reference genome version 1 (Wm82.a1)

2 应用于自然群体数量性状遗传解析

自然群体遗传变异丰富，作物种质资源群体更是品种改良的重要基因资源。全面解析自然群体/资源群体大量存在的QTL及其复等位变异将有助于了解数量性状的遗传规律以及植物遗传改良。Zhang等[21]基于由366份地方大豆材料组成的资源群体，分别使用了RTM-GWAS方法和目前最常用的MLM方法对油脂、油酸和亚麻酸含量进行GWAS分析（表2）。结果显示，在Bonferroni多重测验矫正下，MLM方法对3个性状分别检测到3、18和22个QTL，表型变异解释率分别是19.69%、138.76%和206.52%。可见MLM方法检测的QTL不仅偏少，而且油酸和亚麻酸含量QTL的表型变异解释率还远超过性状遗传率，表明MLM方法中QTL效应估计偏差较大。而RTM-GWAS方法分别检测到50、98和50个QTL，表型变异解释率分别是82.53%、90.29%和83.84%，均小于性状遗传率，结果更为合理。

表2 基于大豆地方品种资源群体的全基因组关联分析方法比较

Table 2 Comparisons between RTM-GWAS and MLM for association results obtained from soybean landrace germplasm population

2：性状遗传率估计；2：QTL表型变异解释率；MLM：混合线性模型方法

2: trait heritability;2: phenotypic variance explained; MLM: mixed linear model

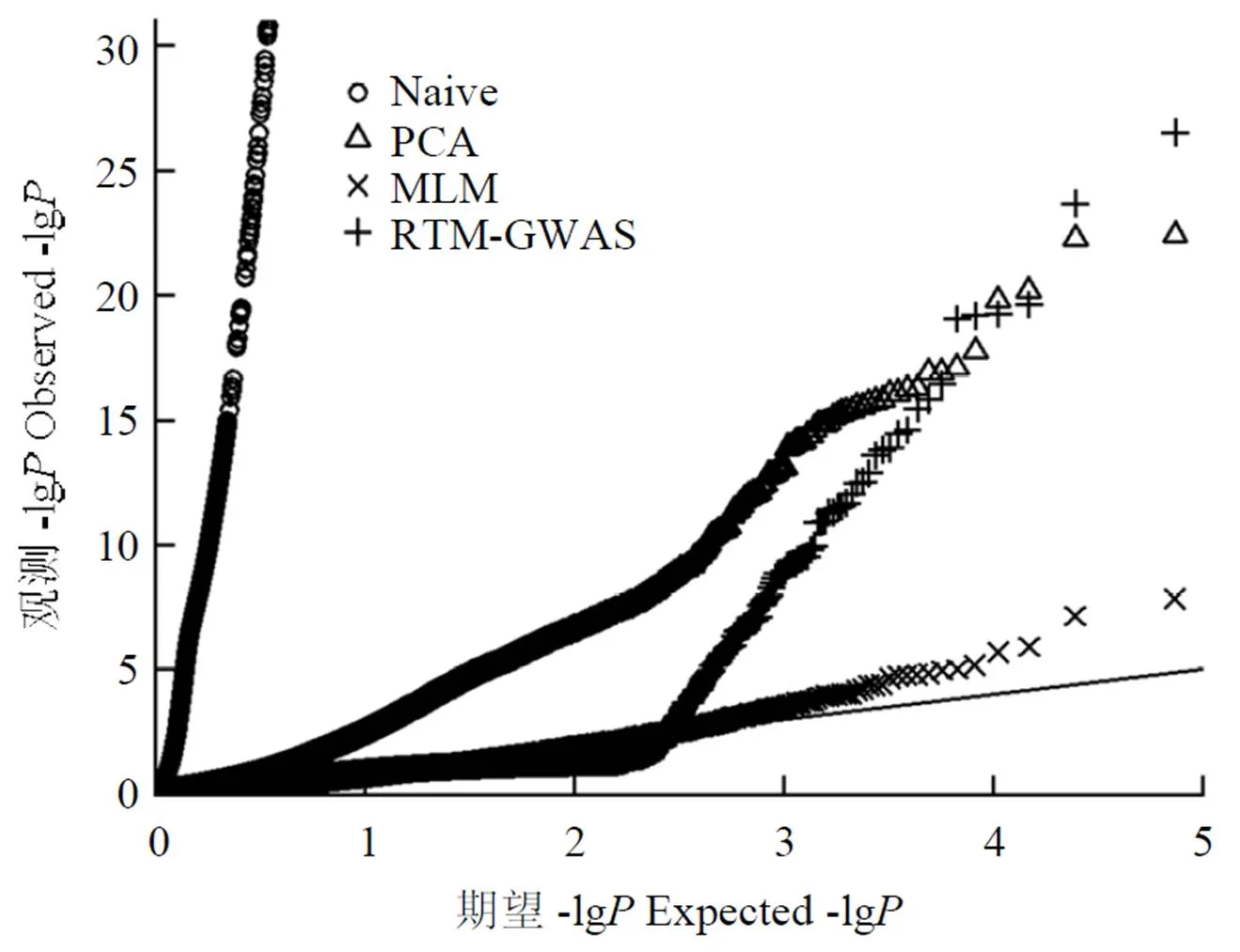
He等[14]对包括1 024份大豆材料的中国大豆种质资源群体的百粒重进行了全基因组关联分析，比较了RTM-GWAS方法与PCA和MLM方法。从分析结果Q-Q图可以看出（图1），未进行群体结构控制的单标记分析方法（Naive）中所有标记都大幅偏离理论值，假阳性非常高，这是因为该群体包括了野生大豆、地方大豆和大豆育种品种，不同材料又收集自不同的大豆生态区，形成复杂的群体结构。通过控制群体结构，PCA方法一定程度上降低了假阳性，但仍远远偏离理论值。MLM方法中所有位点均与理论值较为接近，虽然假阳性大幅降低，但是检测功效也随之降低。RTM-GWAS方法表现则比较合理，大部分位点与理论值接近，检测的QTL大幅高于理论值，既降低了假阳性，又保证了检测功效。

中国大豆种质资源群体中，RTM-GWAS方法共检测到139个百粒重QTL（表1和图2），包括MLM方法检测的3个QTL中的2个，覆盖前人已报道百粒重QTL的73%[14]。RTM-GWAS方法同时估计出139个百粒重QTL上402个等位变异的遗传效应。百粒重QTL及其等位变异效应反应了百粒重性状在群体的遗传构成，所有QTL在群体内材料上的基因型和等位基因效应可进一步构建为性状在群体的QTL- allele矩阵（图3）。QTL-allele矩阵包括了性状在群体内的所有遗传信息，可进一步应用于基因发掘和设计育种。

黑色直线为理论分布参考线

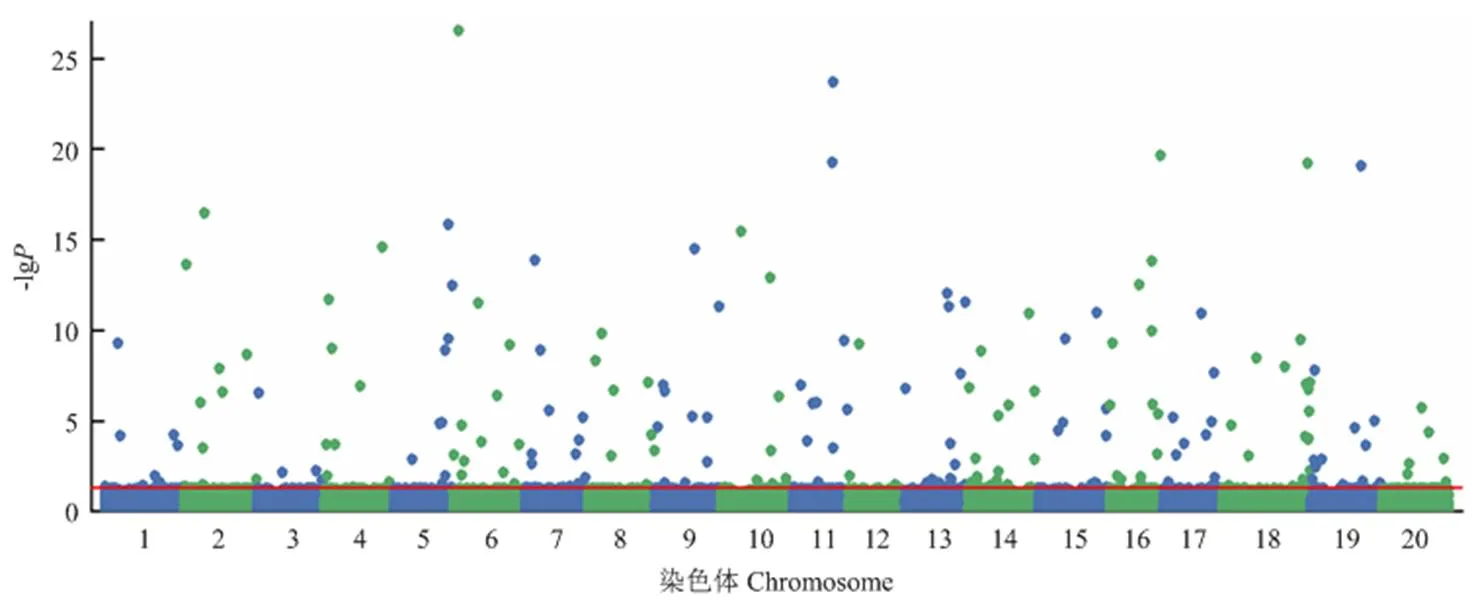
图2 中国大豆种质资源群体百粒重RTM-GWAS分析Manhattan图

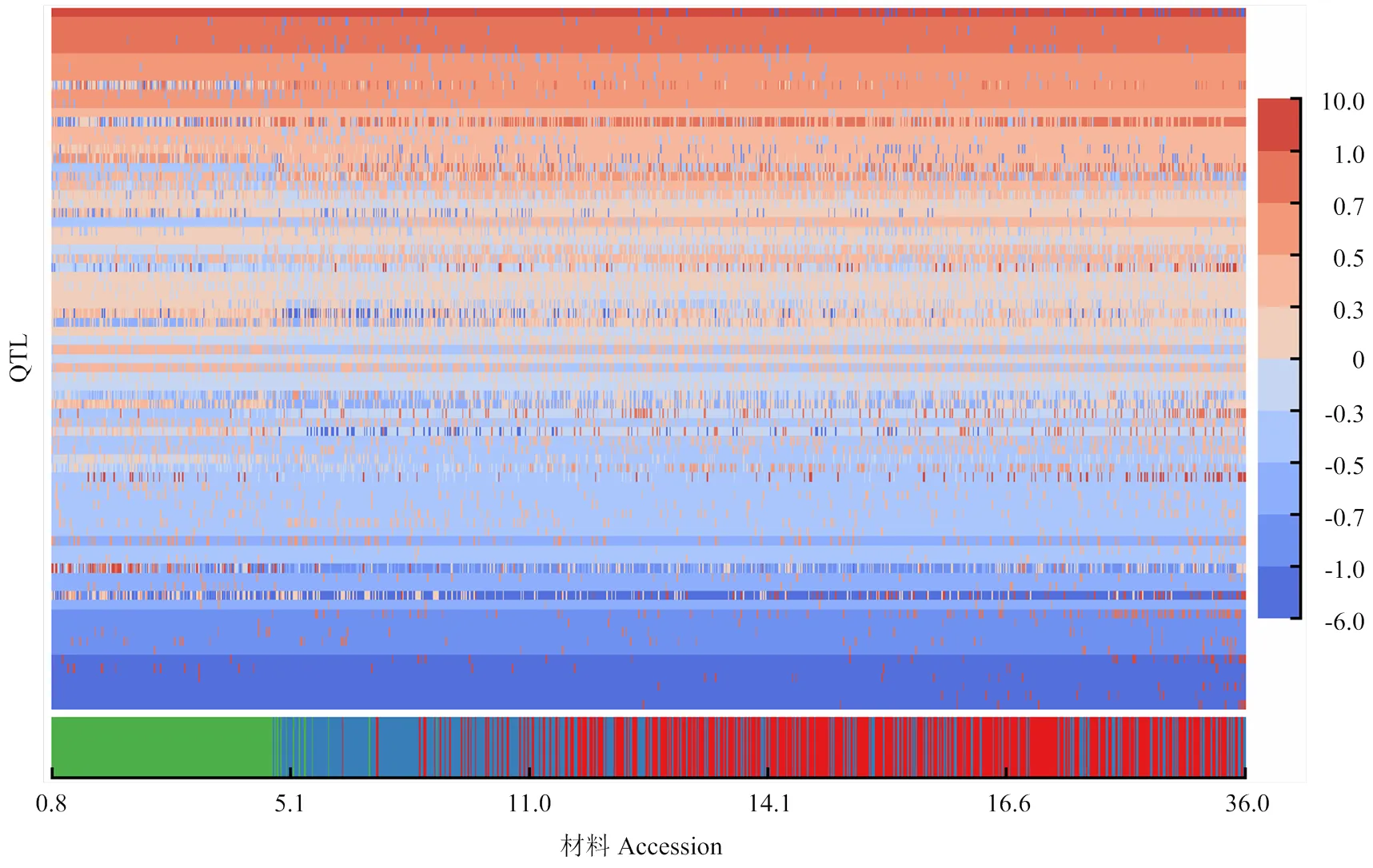
横坐标表示材料，按百粒重升序排列，每一列为一个材料的等位基因组成。纵坐标表示QTL，每一行为一个QTL等位基因在材料中的分布。等位基因效应大小使用颜色表示，暖色表示正效，冷色表示负效，颜色深度表示效应大小

3 应用于RIL和NAM群体数量性状遗传解析

越来越多的RIL群体也开始利用重测序技术获得全基因组高密度SNP分子标记，由于标记密度高，不再需要构建遗传连锁图谱便可以进行QTL检测，此时GWAS方法也可应用于RIL群体。同样，RTM-GWAS也适用于由双亲衍生的RIL群体和由多亲衍生的NAM群体。但是RTM-GWAS中SNPLDB标记根据基因组区段单倍型进行构建，而RIL群体和NAM群体中个体的位点基因型直接来自于亲本，此时SNPLDB标记等位变异应从亲本单倍型中构建。针对RIL群体和NAM群体，RTM-GWAS中SNPLDB标记构建方法作如下调整。首先，仍然使用基于连锁不平衡置信区间的方法确定全基因组范围内的基因组区段。然后将区段内的所有SNP在亲本中组成的单倍型类型作为该位点的等位变异，群体内个体在该位点的基因型由亲本单倍型确定。

Pan等[22]基于大豆RIL群体的分子标记和开花期数据，比较了不同定位方法（CIM、MLM和RTM-GWAS）和不同标记类型（SSR、BIN和SNPLDB）的应用效果。结果显示，3种方法分别检测到10、36、67个BIN-QTL和23、14、86个SNPLDB-QTL。CIM和MLM方法所检测位点的表型变异解释率均超过100%，而RTM-GWAS方法所检测位点的表型变异解释率均小于但接近性状遗传率。因此，RTM-GWAS方法不仅能检测较多的QTL，而且能合理估计QTL表型变异解释率，更适用于RIL群体的QTL定位研究。

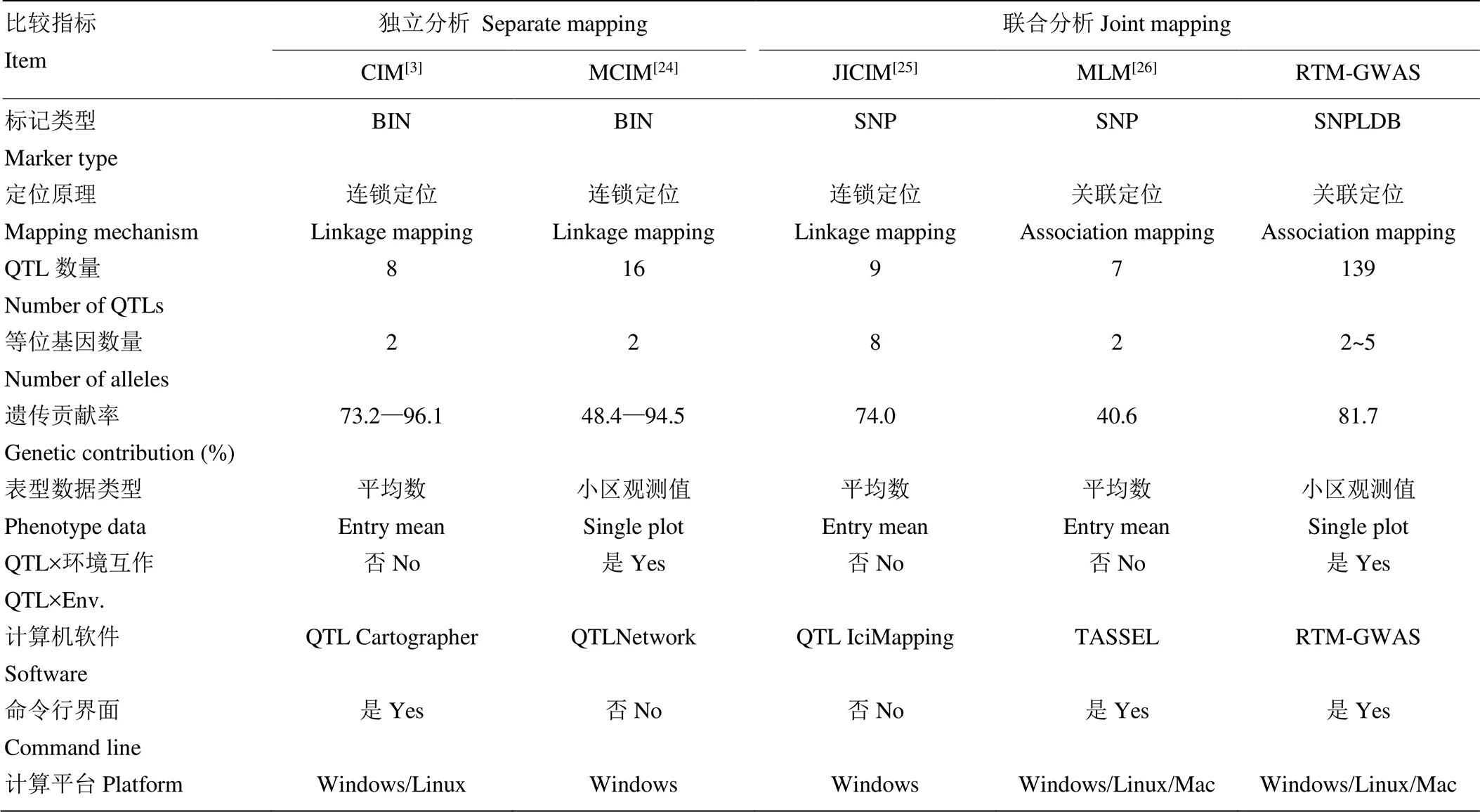
如前所述，尽管NAM群体通过一个共同亲本将多个RIL群体联系起来，提高了群体的遗传变异程度，然而以往分析方法却没将NAM群体作为一个统一完整群体。RTM-GWAS可通过构建SNPLDB标记对NAM群体进行统一分析。Li等[23]基于一个包含4个大豆RIL群体的NAM群体，比较了基于SNP标记的JICIM[6]和MLM方法，以及基于SNPLDB的RTM-GWAS方法（表3）。结果显示，3种方法分别检测到9、7和139个大豆开花期QTL，表型变异解释率分别是74.0%、40.6%和81.7%。该NAM群体有5个亲本，理论上位点上最多存在5个等位基因。而JICIM方法每个位点等位基因数目均为8，MLM方法每个位点等位基因数目均为2，显然不符合实际情况。RTM-GWAS方法每个位点等位基因数目最少2个，最多5个，合理地拟合了群体内的等位基因变异，更适用于NAM群体。

表3 基于大豆NAM群体的五种QTL定位方法特点归纳比较

Table 3 Comparisons of five QTL detection procedures based on soybean NAM population

4 应用于基因与环境互作遗传解析

数量性状不仅受多个QTL的作用，而且还受到QTL之间以及QTL与环境之间相互作用的影响。QTL与环境互作通过维持群体遗传变异在植物环境适应性中起着重要作用。例如，基因与环境互作效应对大豆耐旱性的影响非常大，这是由于干旱程度高度依赖于温度、湿度、降雨等环境因素[27]。因此，更好地了解QTL主效应以及QTL与环境互作效应，对不同环境下育种策略的制定至关重要。然而，以往GWAS通常基于个体表型平均数（最佳线性无偏估计或最佳线性无偏预测），无法解析QTL与环境互作效应。而RTM-GWAS方法基于数量性状的小区观测值，通过QTL与环境互作的多位点模型，不仅能检测主效应QTL，还能够检测仅与环境有交互作用的非主效应QTL。QTL与环境互作线性模型如下：

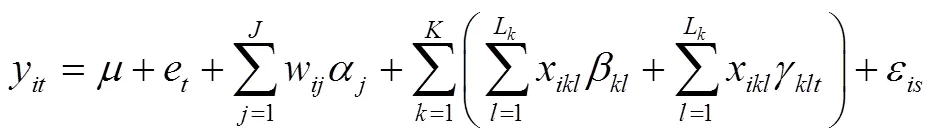
其中，e为第个环境的效应，γ为第个位点上第个等位基因与第个环境的互作效应。其他符号含义同上。RTM-GWAS首先基于模型效应检测QTL，即测验模型中QTL主效应及QTL与环境互作效应的总和是否显著。此时，QTL主效应或QTL与环境互作效应中至少有一项显著时，RTM-GWAS便可以检测出QTL。其次，RTM-GWAS分别对QTL主效应及QTL与环境互作效应进行测验，以确定具体的QTL模型。

Khan等[27]对由2个RIL群体组成的大豆NAM群体进行了苗期耐旱性鉴定，结果显示，对于相对根长和相对茎长，基因型与环境互作效应均极显著。利用RTM-GWAS分别检测到38和73个QTL，其中30和55个QTL主效应解释了26.11%和40.43%的表型变异，16和53个环境互作QTL解释了10.35%的表型变异。结果进一步说明了基因与环境互作效应在大豆耐旱性中起到了重要作用。

5 应用于群体遗传分化与设计育种

RTM-GWAS方法能够较充分的检测出QTL及其相应的复等位变异，由其结果建立的QTL-allele矩阵则代表了群体目标性状的全部遗传组成。因此，QTL-allele矩阵可进一步用于群体目标性状的遗传分化与进化特征与特有与新生等位变异分析。Zhang等[28]基于包括89个大豆蛋白质含量QTL及其255个等位基因的QTL-allele矩阵，分析了地方大豆在不同生态区间的遗传分化特征，发现有32.09%的等位基因为生态区特有，并总结出生态区间遗传分化的4种模式。如图4所示不同生态区间等位基因频率差异不显著和显著的各4个QTL，4个不显著QTL基因频率在6个生态区间相对一致（左边），4个显著的QTL基因频率在6个生态区间差异较大（右边）。这为进一步阐明QTL/基因的进化规律提供了参考。

亲本组配和后代选择是常规育种的2个主要步骤，QTL-allele矩阵则为亲本组配和后代选择提供了理论依据。He等[14]使用RTM-GWAS方法对包含1 024份大豆材料的种质资源群体的百粒重进行了遗传解析，获得了包含139个QTL及其402个等位基因的QTL-allele矩阵，并进一步基于QTL-allele矩阵对所有523 776个单交组合纯合后代群体进行了预测（图5），结果显示部分单交组合后代表现出超亲百粒重，最好的20个组合后代百粒重预测值相比亲本群体提高了12.4%—19.9%（表4）。基于全基因组QTL-allele矩阵的优化组合设计与全基因组选择有本质不同，后者假定全基因组标记均与目标性状相关，通过构建全部标记的预测模型对后代进行预测和选择，因此，需要对育种后代群体进行全基因组标记的鉴定，成本高昂。另外，模型构建所用群体与实际育种群体的差异，还可能导致选择出现严重偏差。由于育种条件的限制，目前，全基因组选择主要应用于动物育种研究。而基于QTL-allele矩阵的选择直接对目标性状位点进行独立选择，更符合实际育种需求，理论上比全基因组选择更加直接和高效。

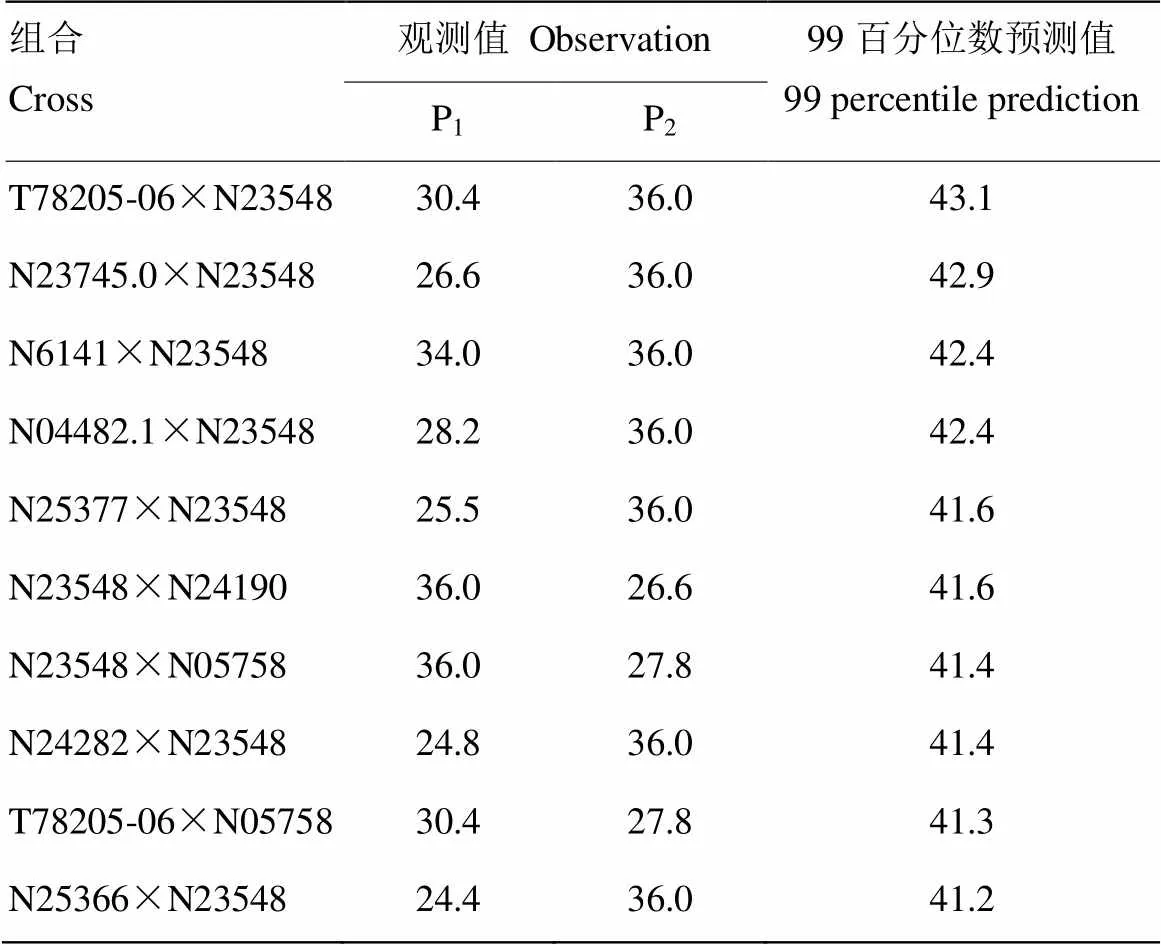
表4 中国大豆种质资源群体百粒重改良优异组合预测

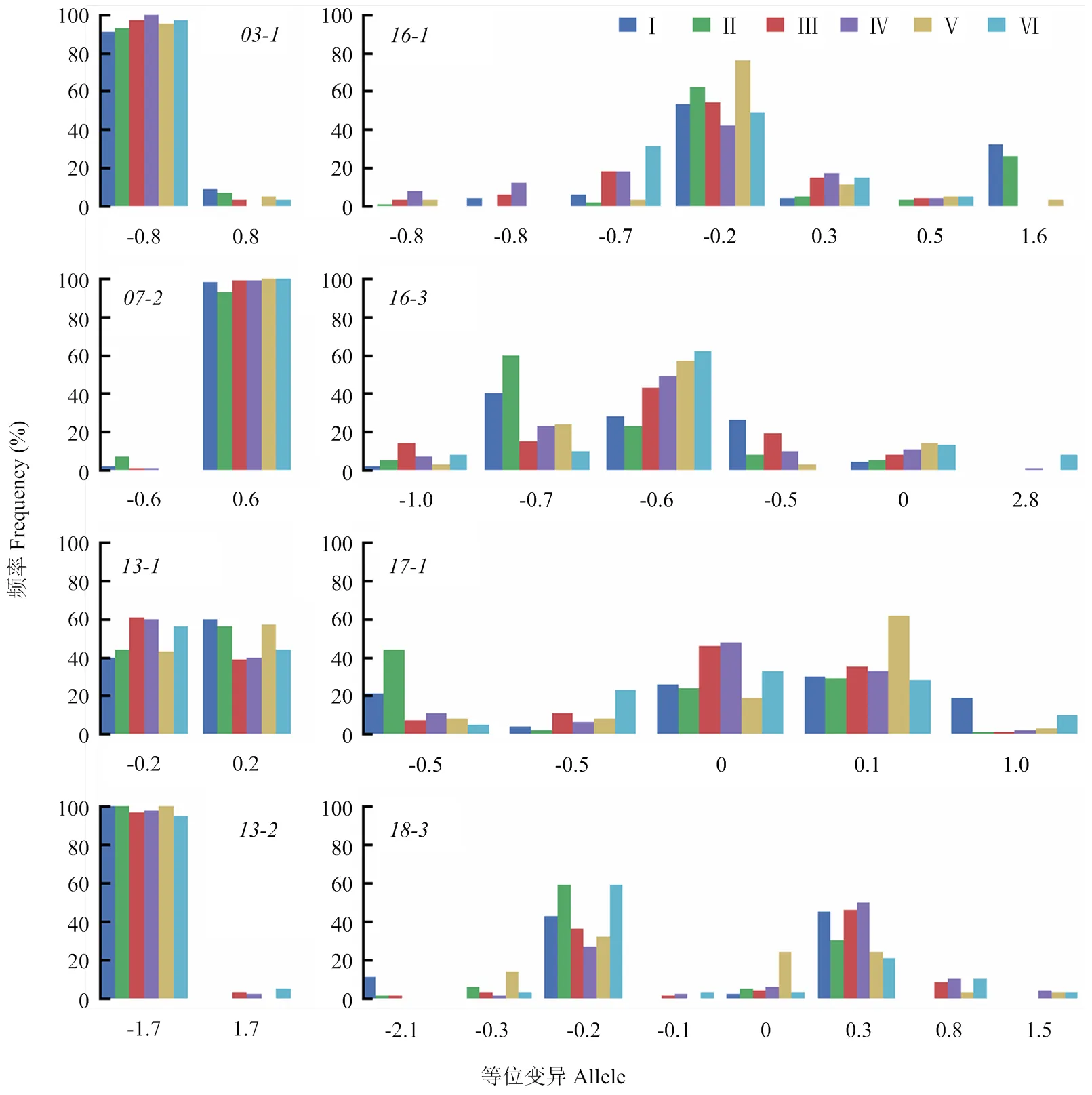
I：北方一熟制春作生态区；II：黄淮海二熟制春夏作生态区；III：长江中下游二熟制春夏作生态区；IV：中南多熟制春夏秋作生态区；V：西南高原二熟制春夏作生态区；VI：华南热带多熟制四季生态区

两条虚线分别表示亲本观测值的最大值（上）和最小值（下）。Min.、P25、P50、P75和Max.分别表示组合后代预测值的最小值、第25百分位数、第50百分位数、第75百分位数和最大值

6 展望

本文中介绍了RTM-GWAS的基本原理和初步应用于植物遗传育种研究的效果。RTM-GWAS方法的最重要特点是能将群体内的QTL及其相应等位变异尽可能多地检测出来，并能给出等位变异的效应及其在群体内的相对频率，因而为全面追踪群体内QTL及其等位变异（基因及其等位基因）的构成和网络结构提供了基本信息，也为群体内QTL及其等位变异（基因及其等位基因）的动态研究（群体遗传学研究）提供了新的工具。

目前，RTM-GWAS方法仅考虑了位点主效应及其与环境互作效应，其分析模型没有包括位点间交互作用（上位性效应）及其与环境互作效应（上位性与环境互作效应）。有研究表明上位性效应对数量性状遗传变异的贡献十分重要，考虑上位性效应的分析模型可以提高表型变异的拟合程度[30]。但是当GWAS模型纳入位点交互作用时，百万级的分子标记数量将导致计算困难，因此GWAS中考虑上位性的研究还非常少[31-32]。针对GWAS上位性效应解析中计算困难的问题，研究者也提出一些高效算法，如BOOST[33]、TEAM[34]等。但是这些方法通常针是对人类疾病-对照（case-control）GWAS而建立的，不能直接用于连续型数量性状，限制了其在植物研究中的应用。因此，探索高效的上位性分析模型将是RTM-GWAS方法下一步需要考虑的问题。由于RTM-GWAS方法的SNPLDB标记具有复等位性，单个标记不能使用一个变量进行表示，进一步增加了上位性模型的复杂程度。另外，随着计算机技术的快速发展，尤其是近几年图形处理器技术的普及应用，将有助于在全基因组水平解析数量性状的上位性效应[35-36]。

复杂性状的遗传构成解析是植物遗传育种研究的基础，不仅可用于进一步研究单个基因的功能，还可用于辅助育种。上文介绍了基于RTM-GWAS解析的QTL及其等位变异的育种优化组合设计，但以往基于RTM-GWAS方法的组合优化设计均针对单个目标性状，而实际育种是对多个性状的综合选择。此时，可利用RTM-GWAS获得的多个目标性状的QTL-allele矩阵对亲本组合后代群体进行预测，获得各个目标性状的预测值。最后，根据实际情况，通过设置性状权重建立多个性状的综合选择指数，进而从多个性状上对亲本组合进行综合选择。优化组合设计是常规育种的第一个主要步骤，实际育种中还需要从后代分离群体中选出优良家系。Meuwissen等[37]提出的全基因选择（genomic selection，GS）方法首先基于参考群体建立分子标记与表型的线性关系，然后在待选群体中利用同一套分子标记信息预测个体的育种值（genomic estimated breeding values，GEBVs），从而达到后代选择的目的。但植物育种中单个组合通常涉及上千个后代个体，目前，实际育种中使用全基因组选择方法进行后代选择花费高昂。在这种情况下，利用QTL-allele矩阵信息进行后代选择可能是另一种有效途径。将基于SNPLDB标记的QTL-allele矩阵用于分子标记辅助后代选择有多种可能的途径：将SNPLDB标记开发为凝胶电泳标记；寻找与SNPLDB标记紧密连锁的凝胶电泳标记；开发SNPLDB标记芯片。

[1] TAM V, PATEL N, TURCOTTE M, BOSSE Y, PARE G, MEYRE D. Benefits and limitations of genome-wide association studies, 2019, 20(8): 467-484.

[2] LANDER E S, BOTSTEIN D. Mapping mendelian factors underlying quantitative traits using RFLP linkage maps, 1989, 121(1): 185-199.

[3] ZENG Z B. Precision mapping of quantitative trait loci, 1994, 136(4): 1457-1468.

[4] YU J, HOLLAND J B, MCMULLEN M D, BUCKLER E S. Genetic design and statistical power of nested association mapping in maize, 2008, 178(1): 539-551.

[5] MCMULLEN M D, KRESOVICH S, VILLEDA H S, BRADBURY P, LI H, SUN Q, FLINT-GARCIA S, THORNSBERRY J, ACHARYA C, BOTTOMS C, BROWN P, BROWNE C, ELLER M, GUILL K, HARJES C, KROON D, LEPAK N, MITCHELL S E, PETERSON B, PRESSOIR G, ROMERO S, OROPEZA ROSAS M, SALVO S, YATES H, HANSON M, JONES E, SMITH S, GLAUBITZ J C, GOODMAN M, WARE D, HOLLAND J B, BUCKLER E S. Genetic properties of the maize nested association mapping population, 2009, 325(5941): 737-740.

[6] BUCKLER E S, HOLLAND J B, BRADBURY P J, ACHARYA C B, BROWN P J, BROWNE C, ERSOZ E, FLINT-GARCIA S, GARCIA A, GLAUBITZ J C, GOODMAN M M, HARJES C, GUILL K, KROON D E, LARSSON S, LEPAK N K, LI H, MITCHELL S E, PRESSOIR G, PEIFFER J A, ROSAS M O, ROCHEFORD T R, ROMAY M C, ROMERO S, SALVO S, SANCHEZ VILLEDA H, DA SILVA H S, SUN Q, TIAN F, UPADYAYULA N, WARE D, YATES H, YU J, ZHANG Z, KRESOVICH S, MCMULLEN M D. The genetic architecture of maize flowering time, 2009, 325(5941): 714-718.

[7] VISSCHER P M, WRAY N R, ZHANG Q, SKLAR P, MCCARTHY M I, BROWN M A, YANG J. 10 years of GWAS discovery: Biology, function, and translation, 2017, 101(1): 5-22.

[8] HUANG X, HAN B. Natural variations and genome-wide association studies in crop plants, 2014, 65: 531-551.

[9] PRICE A L, ZAITLEN N A, REICH D, PATTERSON N. New approaches to population stratification in genome-wide association studies, 2010, 11(7): 459-463.

[10] PRITCHARD J K, STEPHENS M, ROSENBERG N A, DONNELLY P. Association mapping in structured populations, 2000, 67(1): 170-181.

[11] PRICE A L, PATTERSON N J, PLENGE R M, WEINBLATT M E, SHADICK N A, REICH D. Principal components analysis corrects for stratification in genome-wide association studies, 2006, 38(8): 904-909.

[12] YU J, PRESSOIR G, BRIGGS W H, VROH BI I, YAMASAKI M, DOEBLEY J F, MCMULLEN M D, GAUT B S, NIELSEN D M, HOLLAND J B, KRESOVICH S, BUCKLER E S. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness, 2006, 38(2): 203-208.

[13] PRITCHARD J K, STEPHENS M, DONNELLY P. Inference of population structure using multilocus genotype data, 2000, 155(2): 945-959.

[14] HE J, MENG S, ZHAO T, XING G, YANG S, LI Y, GUAN R, LU J, WANG Y, XIA Q, YANG B, GAI J. An innovative procedure of genome-wide association analysis fits studies on germplasm population and plant breeding, 2017, 130(11): 2327-2343.

[15] 贺建波, 刘方东, 邢光南, 王吴彬, 赵团结, 管荣展, 盖钧镒. 限制性两阶段多位点全基因组关联分析方法的特点与计算程序作物学报, 2018, 44(9): 1274-1289.

HE J B, LIU F D, XING G N, WANG W B, ZHAO T J, GUAN R Z, GAI J Y. Characterization and analytical programs of the restricted two-stage multi-locus genome-wide association analysis., 2018, 44(9): 1274-1289. (in Chinese)

[16] GABRIEL S B, SCHAFFNER S F, NGUYEN H, MOORE J M, ROY J, BLUMENSTIEL B, HIGGINS J, DEFELICE M, LOCHNER A, FAGGART M, LIU-CORDERO S N, ROTIMI C, ADEYEMO A, COOPER R, WARD R, LANDER E S, DALY M J, ALTSHULER D. The structure of haplotype blocks in the human genome, 2002, 296(5576): 2225-2229.

[17] GAI J, CHEN L, ZHANG Y, ZHAO T, XING G, XING H. Genome- wide genetic dissection of germplasm resources and implications for breeding by design in soybean, 2012, 61(5): 495-510.

[18] PATTERSON N, PRICE A L, REICH D. Population structure and eigenanalysis, 2006, 2(12): e190.

[19] VANRADEN P M. Efficient methods to compute genomic predictions, 2008, 91(11): 4414-4423.

[20] RISCH N, MERIKANGAS K. The future of genetic studies of complex human diseases, 1996, 273(5281): 1516-1517.

[21] ZHANG Y, HE J, WANG H, MENG S, XING G, LI Y, YANG S, ZHAO J, ZHAO T, GAI J. Detecting the QTL-allele system of seed oil traits using multi-locus genome-wide association analysis for population characterization and optimal cross prediction in soybean, 2018, 9(1793): 1793.

[22] PAN L, HE J, ZHAO T, XING G, WANG Y, YU D, CHEN S, GAI J. Efficient QTL detection of flowering date in a soybean RIL population using the novel restricted two-stage multi-locus GWAS procedure, 2018, 131(12): 2581-2599.

[23] LI S, CAO Y, HE J, ZHAO T, GAI J. Detecting the QTL-allele system conferring flowering date in a nested association mapping population of soybean using a novel procedure, 2017, 130(11): 2297-2314.

[24] YANG J, HU C, HU H, YU R, XIA Z, YE X, ZHU J. QTLNetwork: mapping and visualizing genetic architecture of complex traits in experimental populations, 2008, 24(5): 721-723.

[25] MENG L, LI H H, ZHANG L Y, WANG J K. QTL IciMapping: Integrated software for genetic linkage map construction and quantitative trait locus mapping in biparental populations, 2015, 3(3): 269-283.

[26] BRADBURY P J, ZHANG Z, KROON D E, CASSTEVENS T M, RAMDOSS Y, BUCKLER E S. TASSEL: software for association mapping of complex traits in diverse samples, 2007, 23(19): 2633-2635.

[27] KHAN M A, TONG F, WANG W, HE J, ZHAO T, GAI J. Analysis of QTL-allele system conferring drought tolerance at seedling stage in a nested association mapping population of soybean [(L.) Merr.] using a novel GWAS procedure, 2018, 248(4): 947-962.

[28] ZHANG Y, HE J, MENG S, LIU M, XING G, LI Y, YANG S, YANG J, ZHAO T, GAI J. Identifying QTL–allele system of seed protein content in Chinese soybean landraces for population differentiation studies and optimal cross predictions, 2018, 214(9): 157.

[29] 张英虎. 中国大豆地方品种群体籽粒性状的遗传解析及其在设计育种中的应用[D]. 南京: 南京农业大学, 2014.

ZHANG Y H. Genetic dissection of seed traits of the Chinese soybean landrace population and its utilization in breeding by design [D]. Nanjing: Nanjing Agricultural University, 2014. (in Chinese)

[30] FORSBERG S K, BLOOM J S, SADHU M J, KRUGLYAK L, CARLBORG O. Accounting for genetic interactions improves modeling of individual quantitative trait phenotypes in yeast, 2017, 49(4): 497-503.

[31] MACKAY T F. Epistasis and quantitative traits: using model organisms to study gene-gene interactions, 2014, 15(1): 22-33.

[32] WEI W H, HEMANI G, HALEY C S. Detecting epistasis in human complex traits, 2014, 15(11): 722-733.

[33] WAN X, YANG C, YANG Q, XUE H, FAN X, TANG N L, YU W. BOOST: A fast approach to detecting gene-gene interactions in genome-wide case-control studies, 2010, 87(3): 325-340.

[34] ZHANG X, HUANG S, ZOU F, WANG W. TEAM: efficient two-locus epistasis tests in human genome-wide association study, 2010, 26(12): i217-i227.

[35] SCHADT E E, LINDERMAN M D, SORENSON J, LEE L, NOLAN G P. Computational solutions to large-scale data management and analysis, 2010, 11(9): 647-657.

[36] ZHANG F T, ZHU Z H, TONG X R, ZHU Z X, QI T, ZHU J. Mixed linear model approaches of association mapping for complex traits based on omics variants, 2015, 5: 10298.

[37] MEUWISSEN T H, HAYES B J, GODDARD M E. Prediction of total genetic value using genome-wide dense marker maps, 2001, 157(4): 1819-1829.

Restricted two-stage multi-locus genome-wide association analysis and its applications to genetic and breeding studies

HE JianBo, LIU FangDong, WANG WuBin, XING GuangNan, GUAN RongZhan, GAI JunYi

(Soybean Research Institute, Nanjing Agricultural University/National Center for Soybean Improvement/Key Laboratory of Biology and Genetic Improvement of Soybean (General), Ministry of Agriculture/State Key Laboratory for Crop Genetics and Germplasm Enhancement/Jiangsu Collaborative Innovation Center for Modern Crop Production, Nanjing 210095)

Genome-wide association studies (GWAS) take genome-wide high-density molecular markers to identify associations between genotype and phenotype, which have been widely used for genetic dissection of quantitative traits in plants and animals. However, previous GWAS methods focused on finding a handful of major loci and were not able to detect multi-allelic genetic variation in natural populations based on bi-allelic SNP marker, which caused limitations in extending application of GWAS. The restricted two-stage multi-locus genome-wide association analysis (RTM-GWAS) firstly groups multiple adjacent and tightly linked SNPs based on linkage disequilibrium to form multi-allelic SNPLDB markers with multiple haplotypes as alleles. Secondly, population structure bias is estimated using the genetic similarity coefficient matrix calculated from SNPLDB marker, and the eigenvectors of the similarity matrix are extracted and incorporated as model covariates to correct for population structure bias and to reduce false positives. Finally, RTM-GWAS utilizes two-stage association analysis to detect genome-wide QTLs and their multiple alleles efficiently based on the SNPLDB marker and multi-locus multi-allele model, and builds the final multi-QTL genetic model with the total QTL genetic contribution restricted to trait heritability. RTM-GWAS can also detect QTL-by-environment interaction effect using plot-based phenotype data, and can detect not only the main effect QTL, but also QTL with only interaction effect with environment. RTM-GWAS solves the issue that multiple alleles are not estimable in previous GWAS, and also improves the detection power and reduces the false positive rate by fitting multiple QTLs simultaneously in a multi-locus model. It provides a potential solution for a relatively thorough detection of genome-wide QTLs and their multiple alleles, and the allele effect and relative frequency can also be estimated. From RTM-GWAS results, a QTL-allele matrix can be constructed as a compact form of the population genetic constitution, and can be further used for gene discovery. QTL-allele matrix also provides a new tool for studies on the dynamic change of QTLs and their multiple alleles (genes and their multiple alleles), such as population genetic differentiation and population-specific and new alleles. According to QTL-allele matrix, the progeny genotype of cross between parental lines can be simulated by using computer simulation, and then the phenotype can be predicted to assist optimal cross design and molecular design breeding. In addition, RTM-GWAS is more efficient in QTL detection for bi-parental recombinant inbred line population and multi-parental nested association mapping population because the population structure bias can be well-controlled. The present paper presents the principles and procedures of the RTM-GWAS method at first, and then provides some potential applications of RTM-GWAS in plant genetic and breeding studies.

restricted two-stage multi-locus genome-wide association analysis; multiple alleles; SNPLDB marker; multi-locus model; QTL-allele matrix

10.3864/j.issn.0578-1752.2020.09.002

2019-08-26；

2019-11-30

国家自然科学基金（31701447）、国家作物育种重点研发计划（2017YFD0101500，2017YFD0102002）、长江学者和创新团队发展计划（PCSIRT_17R55）、教育部111项目（B08025）、中央高校基本科研业务费项目（KYT201801）、农业部国家大豆产业技术体系CARS-04、江苏省优势学科建设工程专项、江苏省JCIC-MCP项目

贺建波，E-mail：hjbxyz@gmail.com。通信作者盖钧镒，E-mail：sri@njau.edu.cn

（责任编辑 李莉）