制造商和零售商同时开辟在线渠道下的信息共享价值

赵 静，黄云霞，侯晓瑞，魏丹丹

（天津工业大学 数学科学学院，天津 300387）

供应链成员间实时的信息共享可以有效地减少最终市场需求信息沿供应链向上传递过程中的波动程度（方差）放大现象[1]。在现实中，越来越多的企业已经意识到了供应链绩效和信息共享之间存在着直接的联系，如Wal-Mart 和宝洁公司（P&G）共享了P&G产品的零售信息，Dell 和Cisco 与供应商共享订购量信息。许多文献研究了零售商和制造商单销售渠道供应链下的信息共享问题，如文献[2-5]研究了信息共享策略对供应链成员定价决策和条件期望利润的影响，其中文献[3]通过实证研究发现两家公司之间共享信息的数量由彼此之间关系的好坏决定；文献[6-9]主要研究了不同的信息共享策略对供应量补货策略和库存的影响；文献[10]发现在有固定成本的生产供应链中，当批发价格有很大变化时，制造商受益于信息共享。以上文献大多专注于零售商和制造商在单渠道下的信息共享。

电子商务的迅猛发展推动了企业供应链管理模式的变革，双渠道供应链管理模式被越来越多的企业所认可[11]，其中制造商如IBM 公司、苹果公司等纷纷开辟了在线渠道，零售商如苏宁易购、国美在线等开辟了网上商城。目前，关于制造商开辟双渠道下的信息共享策略对供应链绩效影响的研究比较多，如文献[12-16]考虑了信息共享对制造商利润和零售商利润的影响，其中文献[12]、[14]、[16]研究了零售商愿意共享信息的条件且文献[14]研究了信息共享对制造商开通在线渠道的影响。上述文献大多关注的是制造商开设在线渠道下的信息共享问题，而在制造商和零售商同时开辟在线渠道下的信息共享策略对供应链绩效影响的研究还未出现。

本文考虑制造商和零售商同时开辟在线渠道的的双渠道供应链，制造商与零售商分别对需求信息进行预测，建立了信息共享和信息不共享下的制造商Stackelberg 博弈定价模型，分析了两种模型下定价和期望利润的变化，讨论了零售商愿意共享信息的条件，并通过数值算例得出制造商预测精度和零售商预测精度对供应链成员期望利润的影响。

1 问题描述及假设

考虑由一个制造商和一个零售商组成的双渠道供应链，制造商以单位成本c 生产一种产品，既可以通过在线渠道销售给消费者，也可以通过零售渠道批发给零售商；零售商既可以通过在线渠道销售产品，也可以通过传统渠道销售产品。本文假设制造商和零售商之间具有长期的合作关系，产品的批发价w 相对固定为外生变量。制造商决策在线价p0，零售商决策在线价p1和零售价p2。

本文的需求函数假设为价格的线性函数形式[17-18]，具体地，各渠道需求函数分别表示如下。

制造商的在线渠道需求为：

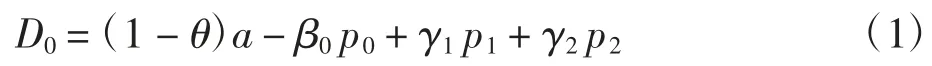
零售商的在线渠道需求为：

零售商的传统销售渠道需求为：

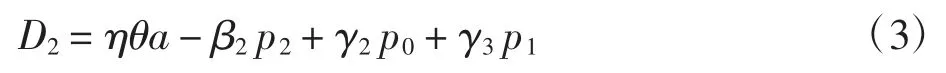
式中：a 为整个市场的基本需求量；θ（θ∈[0，1]）为消费者对制造商零售渠道的偏好；η（η∈[0，1]）为消费者对零售商零售渠道的偏好；参数 βi＞0（i=0，1，2）为渠道需求 Di对自身价格 pi的敏感性程度；γj＞0（j=1，2，3）为渠道需求对交叉价格的敏感性程度，满足以下假设：

假设 1 βi＞ γj＞ 0，i=0，1，2；j=1，2，3。

假设1 保证了渠道需求对自身渠道销售价格的敏感度要大于对其他价格的敏感度，这与现实情况是相符的。假设2 保证了文中各类函数的凹性，即利润函数存在唯一的最大值点。

借鉴文献[16]的研究，假设市场基本需求量a 为随机变量，令其中为市场需求a 的均值，假设制造商和零售商对市场基本需求a的预测值分别为 fm和 fr，并假设 fm=a+ ξm，fr=a+ ξr。其中且独立于 a。预测误差ξm和ξr是相关的且相关系数为ρ。假设协方差不大于方差，即

零售商基于自身预测值fr下a 的条件期望值为：

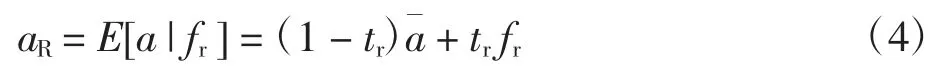
制造商基于自身预测值fm下a 的条件期望值为：

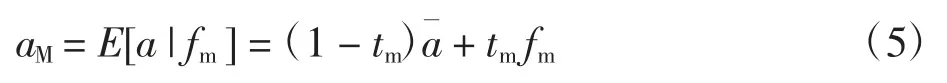
信息共享后在fr和fm条件下对需求a 的预测值为：

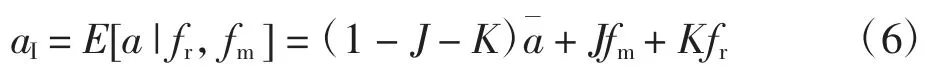
在观察到制造商的预测值后，零售商预测值的条件期望为：

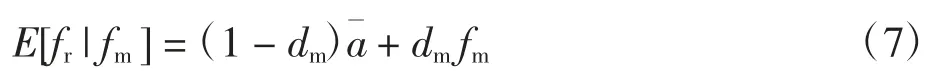
信息共享前制造商以fm为条件模拟的信息共享情况下a 的期望为：

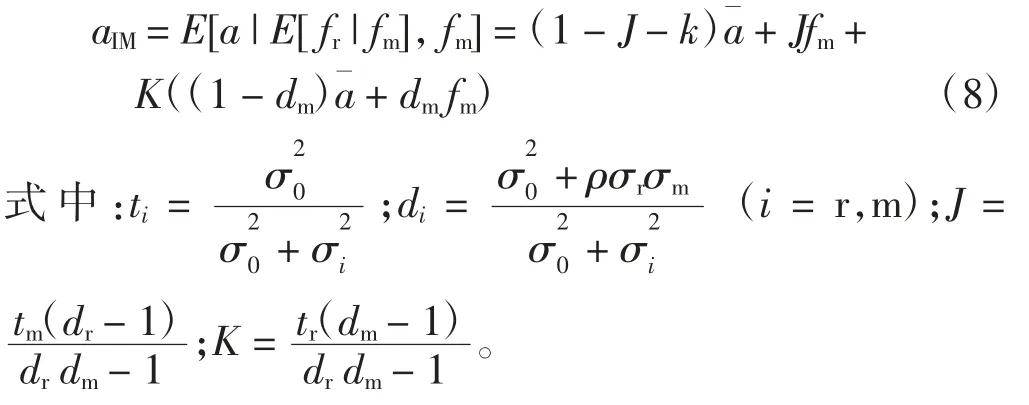
可以证明[16]：aIM=aI，故下文均以 aI代替aIM。基于以上描述和假设，制造商和零售商的利润函数分别为：

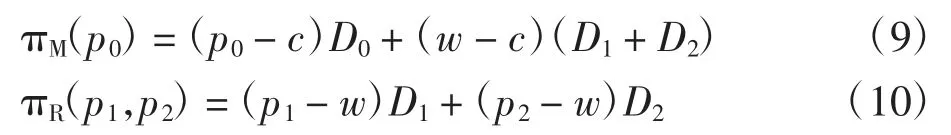
2 模型建立和决策分析

2.1 信息共享（S）

考虑零售商与制造商共享需求预测信息，建立制造商主导的Stackelberg 博弈模型如下：

采用逆向递推法求解此动态博弈模型，可得最优定价策略，如定理1。

定理1在信息共享情况下，制造商最优在线价零售商最优在线价和零售商最优零售价分别为：

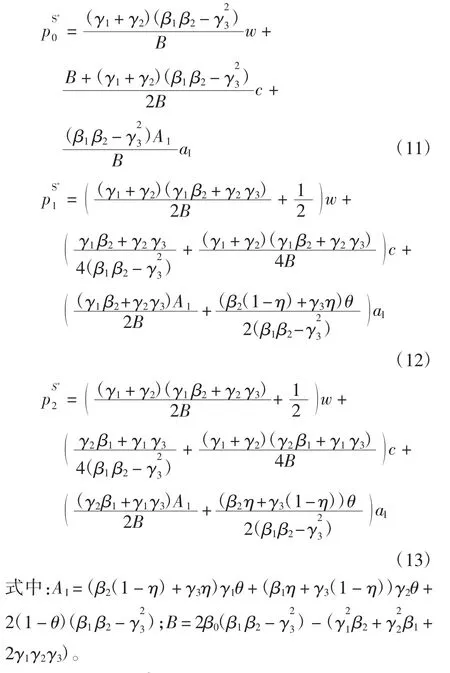
证明：对求关于 p1和 p2的一阶偏导数得：

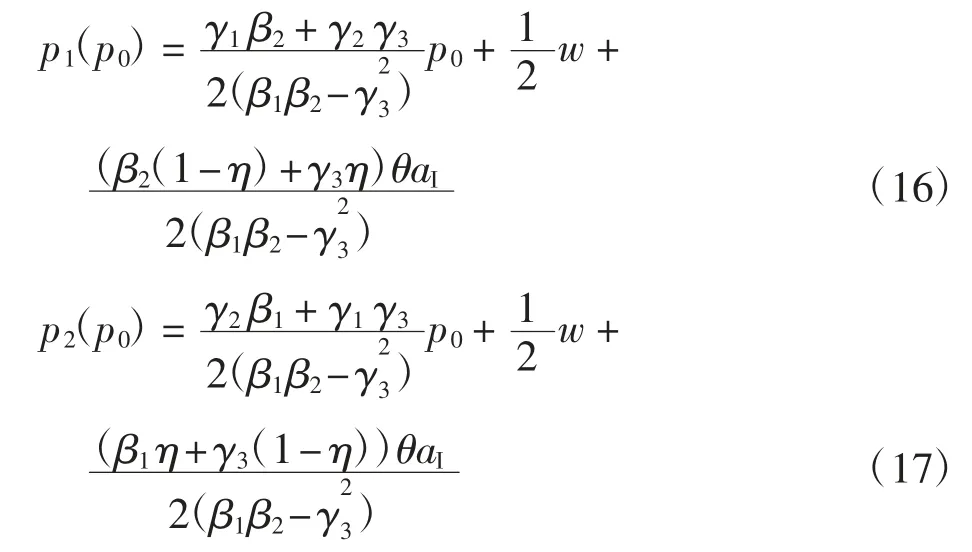
2.2 信息不共享（N）

考虑零售商与制造商不共享预测信息，建立制造商主导的Stackelberg 博弈模型如下：

采用逆向递推法求解此动态博弈模型，可得最优定价策略，如定理2。

定理2在信息不共享情况下，制造商最优在线价零售商最优在线价和零售商最优零售价为

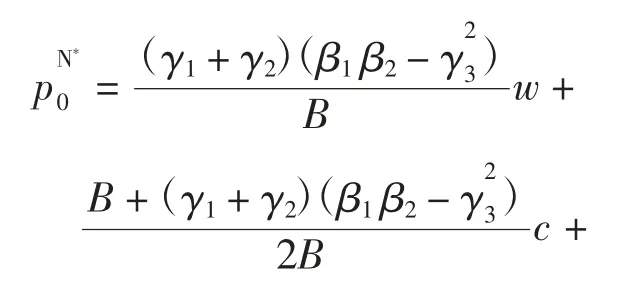
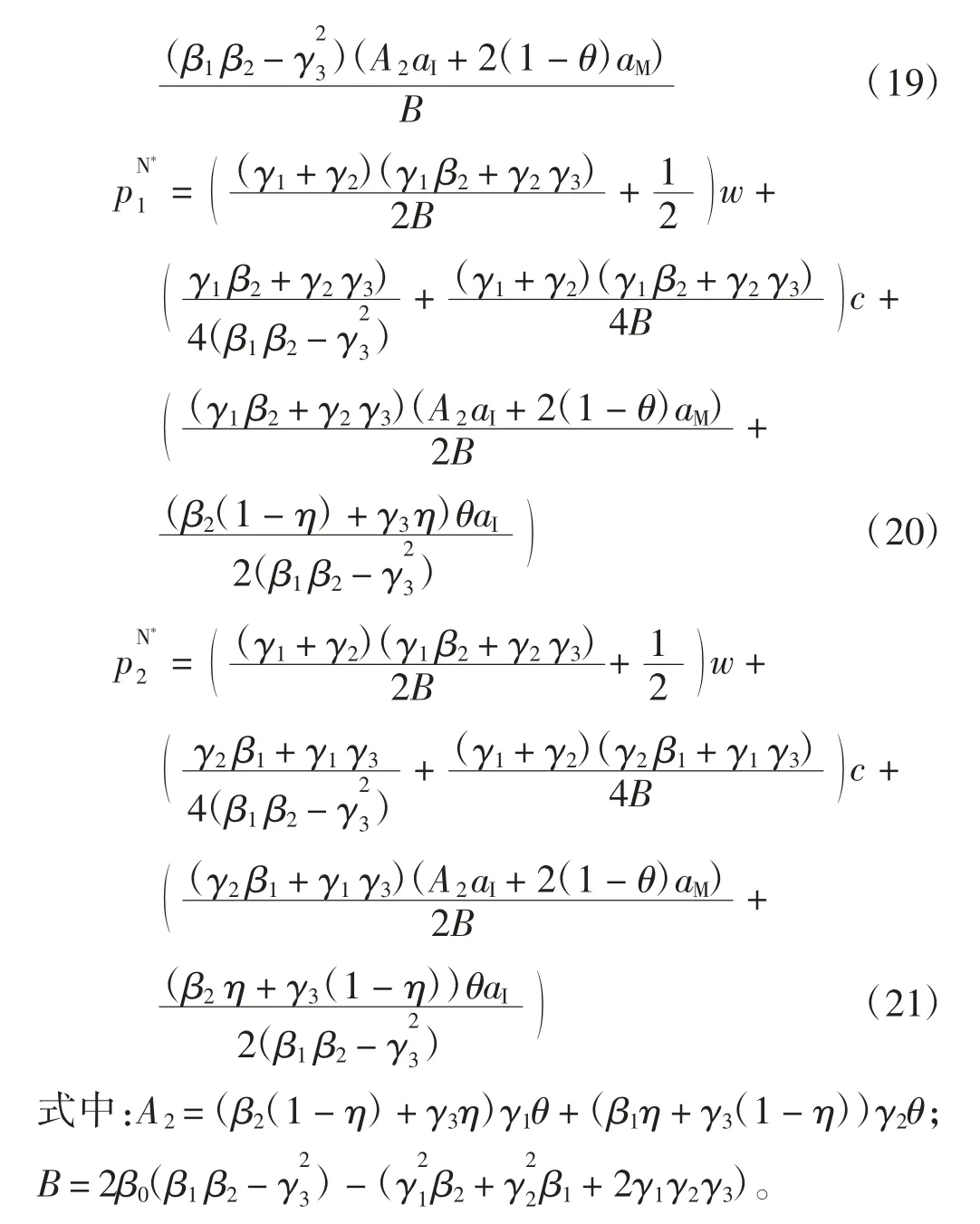
证明：在制造商主导的Stackelberg 博弈下，制造商先给出价格策略，零售商可据此获知其预测信息，故此时的目标函数为零售商的最优反应函数由式（16）、式（17）给出，将其代入中，并对p0求一阶导数可得：

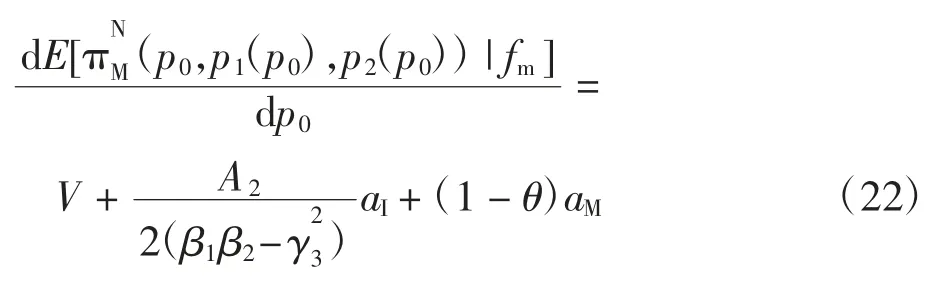
2.3 信息共享价值分析

由于所得均衡解较为复杂，为了更好地比较结果，本节假设价格敏感性参数相等，即β0=β1=β2=β，γ0=γ1=γ2=γ，通过比较信息共享和信息不共享情形下的最优定价策略，分析得出信息共享对供应链成员的定价策略和最大期望利润的影响，见结论1、结论2。

结论1信息共享后制造商的最优在线价，零售商的最优在线价和零售价的增值分别为

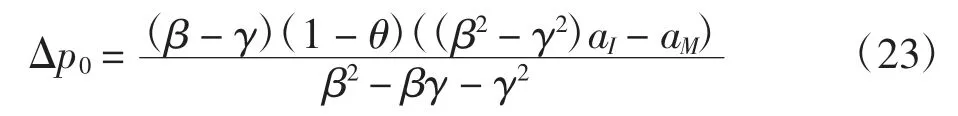
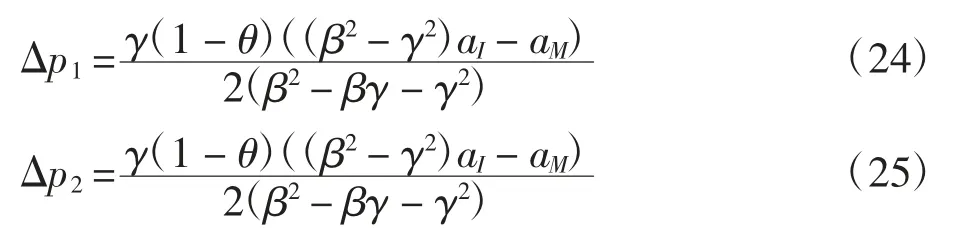
由结论1 可知，信息共享对最优销售价格的影响取决于（β2- βγ- γ2）与（（β2-γ2）aI-aM）的正负。当 β2-βγ - γ2＞ 0 且（β2- γ2）aI＞ aM时，或当 β2- βγ-γ2＜ 0 且（β2- γ2）aI＜ aM时，信息共享情形下制造商和零售商的最优售价均大于信息不共享情形下的最优售价；否则，信息共享情形下制造商和零售商的最优售价小于信息不共享情形下的最优售价。易见Δp1=Δp2，这说明信息共享对零售商最优在线价和最优零售价的影响相同；由可知，信息共享对制造商最优售价和零售商最优售价的影响成正比关系。另外，由参数假设易得，当 β2- βγ - γ2＞ 0 时信息共享后的条件期望值aI对最优售价的增值为正影响，而制造商基于自身信息的条件期望值aM对最优售价的增值为负影响；当 β2- βγ - γ2＜ 0 时结论相反。

结论2信息共享对制造商、零售商和整个供应链期望利润的增值分别为ΔΠM、ΔΠR和ΔΠ，表达式为：

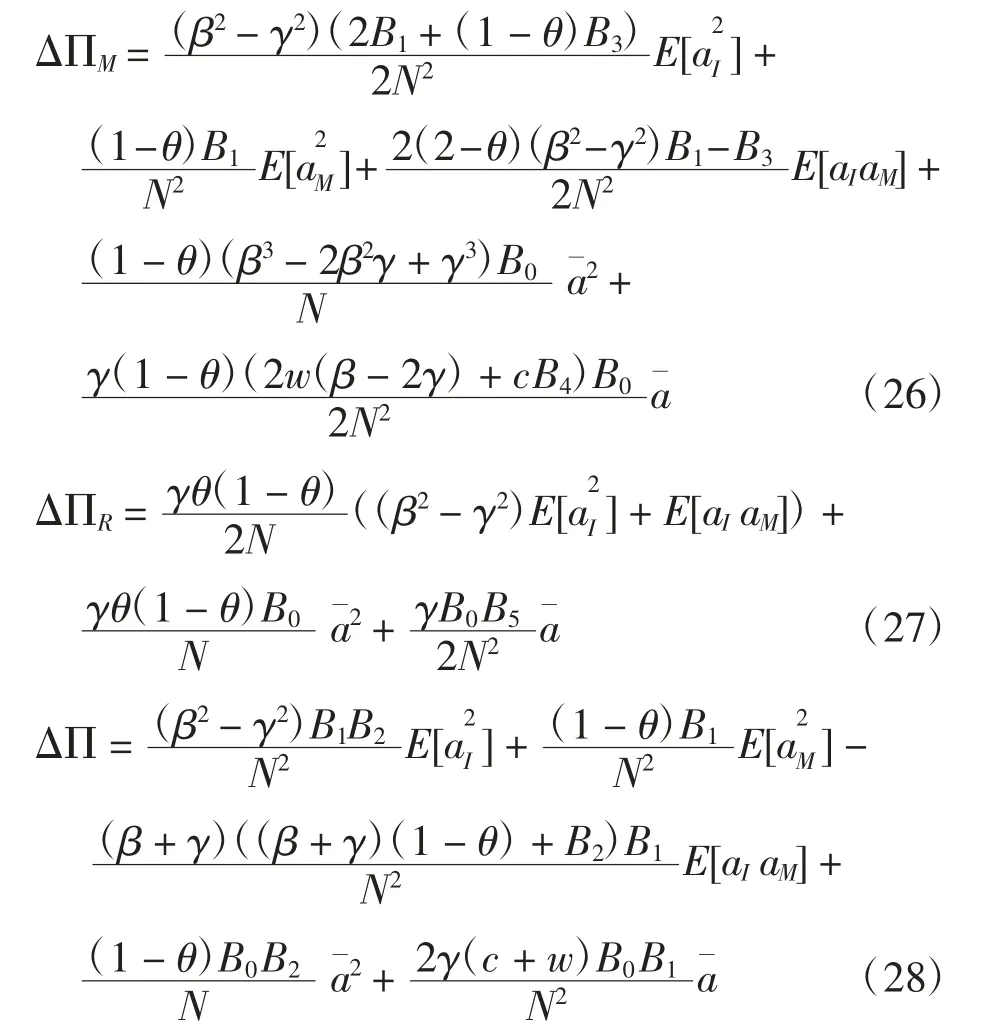
式中：B0=1- β2+ γ2；B1=（1- θ）（β2- γ2）（β -2γ）；B2=γ（1-2θ）-β（1-θ）；B3=θ（β3（-2β2+6β+2γ2）+γ2（β+γ+8γ3）+β2（14γ3+γ））；B4=4β3-7β2γ-3βγ2+5γ3；B5=2w（β-γ）（β2-γ2）-c（β2+βγ-3γ2）；N=β2-βγ-γ2.

由结论 2 看出，ΔΠM、ΔΠR与 ΔΠ 解析形式比较复杂，其正负依赖于模型参数。本文参考文献[5]中的方法进行讨论分析。考虑参数满足如下条件：（i）ΔΠM＞0，ΔΠR＞ 0；（ii）ΔΠ ＞ 0，但 ΔΠM或 ΔΠR有一小于 0；（iii）ΔΠ ＜0。当参数取值满足条件（i），信息共享对制造商和零售商都是有利的，二者自愿共享信息；当参数取值满足条件（ii），信息共享对整个供应链是有利的，但对一方有利，一方不利，此时，获益方可采取信息共享合同促使信息共享的实施；若参数取值满足条件（iii），说明信息共享对整个供应链是不利的，不共享信息是制造商和零售商的最优策略。

3 数值算例分析

为了获得更多的管理启示，本节通过数值算例分析预测精度对最大期望利润的影响。制造商预测标准差σm和零售商预测标准差σr对制造商期望利润、零售商期望利润和供应链整体利润的影响如图1、图2所示。参数取值为=90，β=0.6，γ=0.2，η =0.4，θ=0.7，c=5，σ0=30，σr=15（5-30），w=10，ρ=0.1，σm=15（5-30）。其中，（5-30）表示预测标准差的取值变化范围。

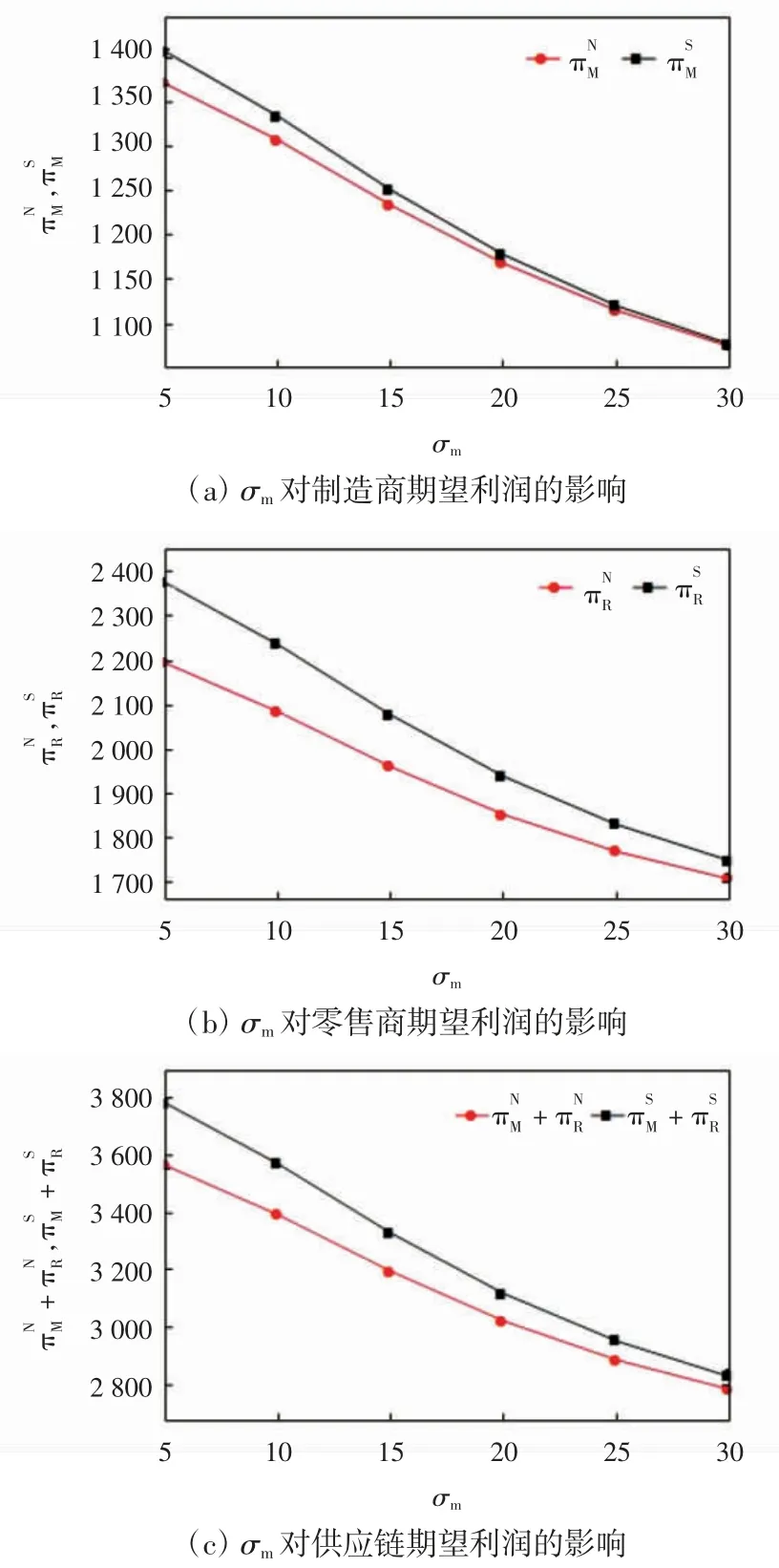
图1 σm 对最大期望利润的影响Fig.1 Effect of σm on maximum expected profit

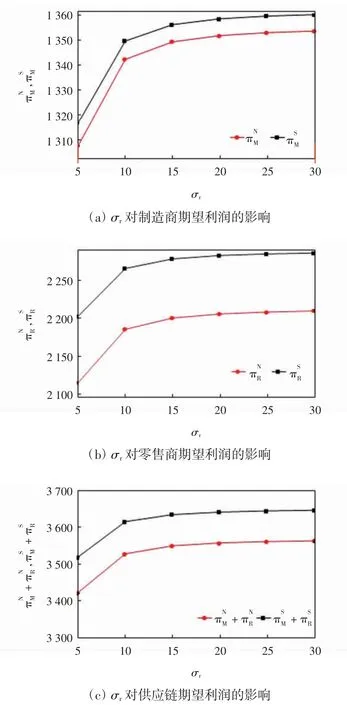
图2 σr 对最大期望利润的影响Fig.2 Effect of σr on maximum expected profit

由图1 可以看出，随着制造商预测精度的增加（即σm减小），制造商利润、零售商利润和供应链总利润随之增加。这与我们的直觉是一致的，制造商预测精度增加，意味着可以获得更准确的预测信息，从而可以增加各方的利润。

由图2 可以看出，随着零售商预测精度的减小（σr增加），制造商利润、零售商利润和供应链利润随之增加。这是因为当零售商对市场的预测不准确时，零售商有可能会把销售价定的过低，使销售量增加，导致利润增加。由于需求增加间接导致制造商批发给零售商产品所获利润增加，从而供应链总利润增加。

由图1 和图2 可以看出，不论σm和σr如何变化，信息共享情形下的供应链成员利润总是高于信息不共享情形下的利润。此组参数满足条件（i）ΔΠM＞0，ΔΠR＞0，信息共享对制造商和零售商都有利。

4 结论与展望

本文考虑了由一个制造商和一个零售商同时开辟在线渠道的双渠道供应链，针对制造商和零售商对市场需求的预测分别建立了信息共享和信息不共享情形下的制造商主导的Stackelberg 博弈定价模型，分析比较了两种情形下的定价策略及利润的变化。给出了信息共享对供应链成员的定价策略和最大期望利润的影响，讨论分析了实施信息共享的参数满足条件。理论分析表明：信息共享对零售商最优在线价和最优零售价的影响相同，对制造商最优售价和零售商最优售价的影响成正比；在一定的参数条件下，信息共享情形下的最优售价大于不共享情形下的最优售价。通过数值算例，分析了制造商和零售商预测精度对最大期望利润的影响，并验证了理论分析的正确性。

本文只考虑了信息共享策略下的一种分散决策博弈定价问题，且制造商生产单一产品。考虑制造商生产多产品的信息共享问题和博弈定价问题是将来研究的方向。