基于流形结构重建的多目标气动优化算法

宋超，李伟斌，周铸，刘红阳，蓝庆生

中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

飞行器气动外形的优化设计必须考虑多个目标，例如，民用飞机需要综合考虑巡航升阻比、阻力发散、力矩特性以及抖振边界等问题[1]，直升机旋翼需要在悬停、前飞和机动等多种运动状态下有优良的高速超临界性能、低速大迎角气动性能，以及接近于零的力矩系数[2]。然而，多个目标往往是互相矛盾的，一个目标的提升可能是以另一个目标的妥协为代价[3]，因此需要一种全面衡量所有设计目标的系统设计方法。

Fonseca和Fleming[4]利用Pareto最优解集概念，提出了多目标遗传算法(Multi Objective Genetic Algorithm, MOGA)。随后，Srinivas和Deb[5]提出了非劣分层遗传算法(Non-dominated Sorting Genetic Algorithm, NSGA)。该算法基于非支配排序思想设计，能够有效解决多目标设计问题，得到均匀分布的解。Deb等对NSGA进行改进，并提出了基于精英保留策略的非劣排序进化算法(NSGA2)[6]，与NSGA相比，NSGA2的计算复杂度有所降低，并且种群的分布更加均匀。此类传统的多目标进化算法已经广泛应用于飞行器的多目标优化设计中[7-11]，并取得了一定的成果。然而，演化多目标优化算法具有一些固有缺点，比如当种群接近收敛时，盲目交叉、变异操作会使本已近似收敛的种群偏离实际的Pareto解集(Pareto Set, PS)，给算法性能造成不良影响[12]。

分布估计算法(Estimation of Distribution Algorithm, EDA)[13]通过建立解集分布的概率模型，然后在该模型上随机产生新的子代个体，从而实现种群进化，避免了传统的交叉变异操作。EDA凭借其高效优化思想，已经成了多目标优化领域的研究热点之一[14-15]。Zhang等[16]利用设计空间的Pareto解集是一个分段连续的k维流形(k=m-1，m为设计目标个数)这一规律[17]，发展了基于规则模型的多目标EDA。如何建立解集分布的概率模型，是EDA的核心问题。一些建模方法，如主成分分析(Principal Component Analysis, PCA)[18]等需要对种群进行聚类，过程复杂且准确度不高。詹炜[19]利用局部线性嵌入(Locally Linear Embedding, LLE)方法发掘Pareto前沿的流形结构，进行了卫星星座的多目标优化设计，取得了较好的效果。Yang[20]等采用LLE和免疫克隆算法来发掘Pareto前沿结构。目前，基于流形结构的EDA在气动多目标优化问题中的应用还在初步研究阶段。本文提出一种利用流形结构重建的分布估计算法，将其用于多目标气动优化问题，可显著提高优化效率，实现多目标气动优化问题的高效求解。

1 算法介绍

分布估计算法首先建立一个描述解集分布的概率模型，在此基础上对概率模型进行采样，得到新的解集分布，如此反复进行，实现种群的进化，直到终止条件[21]。本文采用流形结构重建的方法来建立概率模型，并对目标空间的Pareto前沿进行扩展以实现概率模型的采样，实现了基于流形结构重建的多目标优化算法。

1.1 流形结构重建算法

优化算法迭代过程中的种群逐渐形成清晰的Pareto前沿，高维设计空间中的Pareto解集存在一定的相关性和规律性。根据卡罗需-库恩-塔克条件(Karush-Kuhn-Tucker condition， KKT)[16]，设计空间的Pareto解集是一个分段连续的低维流形。若获得低维流形表示，可挖掘出其中蕴含的信息，进而指导优化算法的演化。另一方面，由于低维流形的简单性，一定程度上解决了高维设计变量带来的诸多问题，如维数灾难。

已有的利用流形结构的多目标优化算法，借助了流形学习算法来发掘其流形结构。大多数流形学习算法，如前面提到的PCA、LLE等方法，都只是将高维空间中的样本数据点投影到低维流形上，投影关系并没有具体的解析函数表达式。具体地，针对气动优化问题，虽然可以采用流形学习算法将设计空间中的样本点投影到低维的流形空间，但在低维流形空间中的点不具有物理意义，直接利用这些信息是困难的。即低维流形空间中的任意坐标不能显式地对应于设计空间中的点，因此也就无从求得对应的气动力。

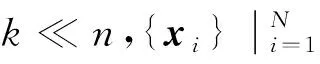
x=g(y)=xi+J(yi)(y-yi)+R(y,yi)

(1)

式中：J(yi)为函数g(y)在点yi的雅克比矩阵；R(y,yi)为余项。略去余项并假设xi有z个邻域点，则有

(2)

(3)

至此得到了点yi的雅克比矩阵J(yi)。

对于流形空间Sk中的任意一点y，解出其在高维空间Dn中坐标x的过程称为流形结构重建。对应于气动优化问题，即给定目标空间中的一点，求其设计空间中的坐标。流形结构重建的具体步骤如下：

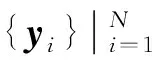
步骤2 找出ys在高维空间Dn中的坐标xs,xs的邻域点xs,1,xs,2,…，xs,z以及这些邻域点在Sk中的坐标ys,1,ys,2, …，ys,z。

步骤4 点y在Dn中的坐标x≈xs+Qs(y-ys)。

值得注意的是，以上流形结构重建算法建立的高维流形空间与对应的低维表示空间的显式映射关系，是基于流形结构的连续性、局部等距性等一系列假设的，更详细的约束条件及过程推导见文献[22]。

1.2 目标空间Pareto前沿扩展

利用1.1节的流形结构重建算法，可以得到低维目标空间到高维设计空间的映射关系。通过在目标空间Pareto前沿的扩展就可以得到对应的设计空间的解集分布，用于指导算法进化。生成新个体的算法如图1所示。设ζ为流形结构，将种群个体看作是一个随机变量ξ的独立观测量，且ε是一个符合正态分布的随机噪声向量。种群个体在ζ附近随机分布为

ξ=ζ+ε

(4)

这一方法也被Zhang等[16]、詹炜[19]采用。本文直接在目标空间对Pareto前沿进行“扩展”，一方面极大简化了算法，另一方面目标函数空间中的流形结构有清晰的物理意义，能够指导算法演化。

一般地，假设希望达到比当前最优Pareto前沿上目标函数更小的值，随机向量ε取值为

(5)

式中：上标i表示向量的第i个分量；N(yi)为均值为1、方差为1的正态分布函数；κ为推进因子。

图1 流形结构扩展示意图Fig.1 Illustration of manifold structure extension

1.3 基于流形结构重建的多目标优化流程

本文采用流形结构重建算法估计解集的概率分布，利用Pareto前沿的流形分布规律，用于指导多目标优化算法的演化，以下称该算法为MR-EDA。记算法种群为

Pop(t)=[x1,x2,…，xN]

(6)

式中：t为当前迭代步数；N为种群大小。个体适应度值F(x)=[f1(x),f2(x),…，fm(x)]Τ，m为目标个数。采用MR-EDA法的优化流程如图2所示，具体如下：

步骤1 产生初始种群Pop(0)，计算种群中的每个个体的适应度值F(x)。

步骤2 对当前种群进行非支配排序，选取前N1个个体，组成新的种群Q(t)。针对Q(t)，利用1.2节所述的流形结构重建算法，生成N2个个体，形成种群P(t)。其中N=N1+N2。

步骤3 若满足停止条件，迭代结束。否则，Pop(t)=Q(t)+P(t)(t=t+1)，返回步骤1继续进行迭代。

图2 MR-EDA优化流程图Fig.2 Flowchart of MR-EDA optimazation

2 解析函数测试算例

ZDT测试集是目前广泛采用的两目标测试函数。本文选取了ZDT1、ZDT2、ZDT3作为测试函数，其中ZDT1的最优前沿为凸函数，ZDT2的最优前沿为凹函数，ZDT3的最优前沿为分段凹函数。测试函数的定义如表1所示，其中自变量维数m均取为30。

表1 测试函数定义Table 1 Definitions of test functions

注：上标1表示矢量的第1个维度的值。

为评价算法性能，引入IGD(Inverted Generational Distance)指标[23]。该指标首先需要均匀分布在真实Pareto最优前沿上的点集S*，设S为优化算法得到的Pareto非支配解集，则IGD定义为

(7)

式中：d(v,S)为点v到解集P所有解中的最小距离；|S*|为样本集S*中的点数。IGD指标能同时度量收敛性和多样性。越小的IGD值表示优化算法得到的非支配解越逼近真实最优解，同时非支配解的均匀性也越好。

本文分别采用MR-EDA与NSGA2进行解析函数的优化测试。设计变量数目为30，初始种群数目为100，最大迭代步数设为200。NSGA2的交叉概率为0.8，变异概率为0.3。MR-EDA中流形重构种群数目N1=N/2。推进因子κ的取值过小可能影响收敛效率，取值过大则不满足流形重构的条件，经测试κ=0.05取得较好的效果。因此，本文算例中推进因子κ均取为0.05。图3(a)给出了测试函数ZDT1的优化结果，分别给出了ZDT1函数的真实最优Pareto前沿，NSGA2及本文算法MR-EDA得到的最优Pareto前沿。如图3(a)所示，本文所提算法优化得到的Pareto最优前沿与真实前沿几乎重合，并且在Pareto解的分布更加均匀。经过相同迭代步数的NSGA2得到的最优Pareto前沿与真实Pareto前沿还有一定的距离。图3(b)给出了ZDT2测试函数的优化结果。类似于ZDT1优化结果，本文算法得到的ZDT2函数最优Pareto前沿相比NSGA2收敛更好，前者基本与真实Pareto前沿重合。图3(c)为ZDT3函数的测试结果，经过200步的迭代，本文算法及NSGA2均未收敛到真实Pareto前沿，但本文算法明显地得到了更好的Pareto解集。

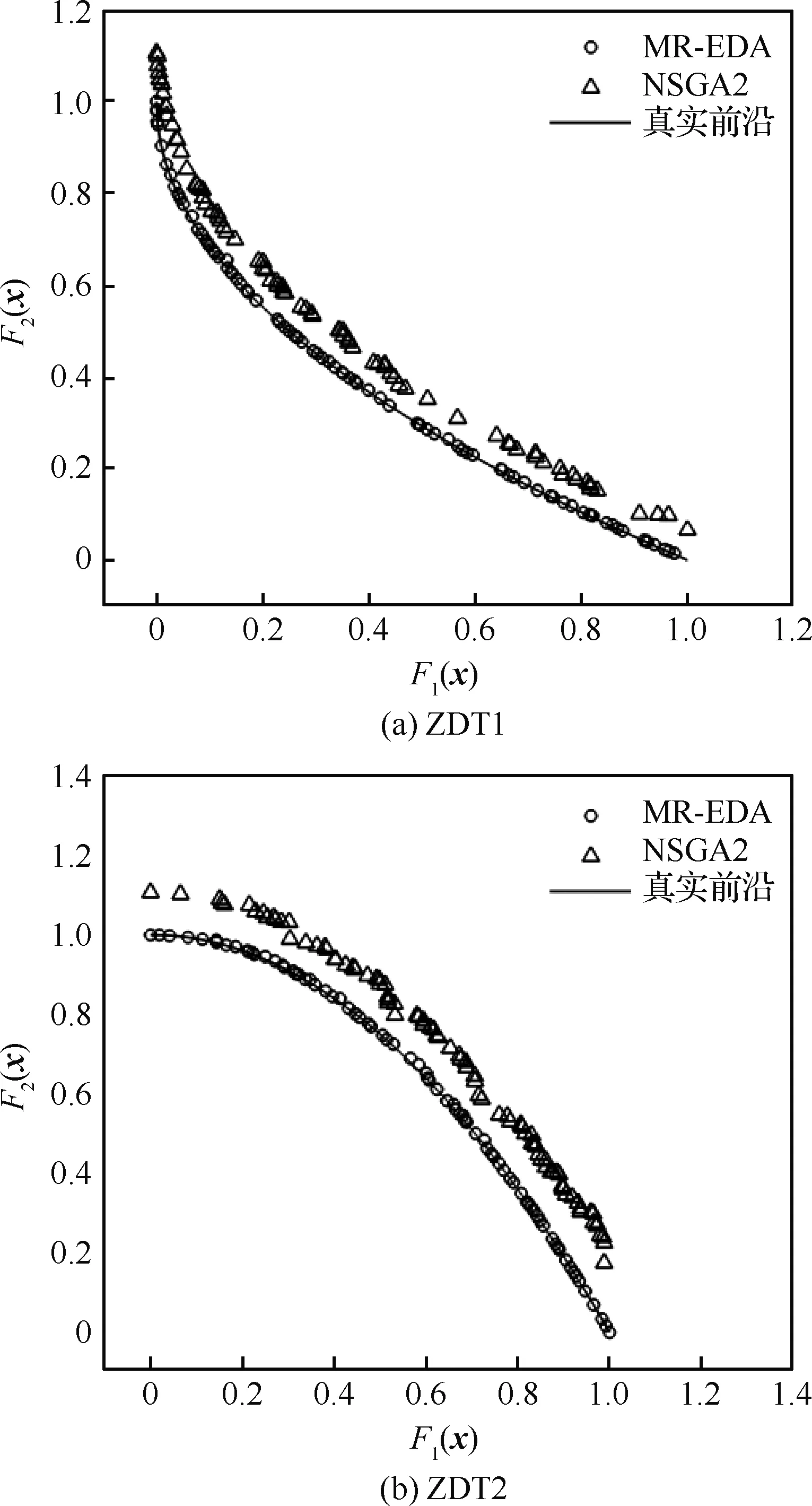
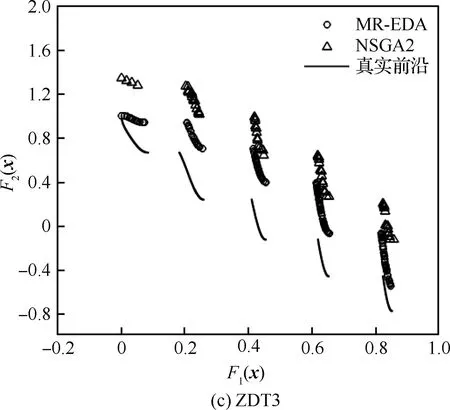
图3 3种测试优化算例的Pareto前沿Fig.3 Pareto fronts obtained by three test optimization examples

图4给出了3种测试优化算例的IGD指标收敛过程。从图中可以看出，本文算法的IGD指标收敛更快，对于ZDT1与ZDT2，其IGD分别在约150步和110步时几乎收敛到0。对于ZDT3，本文算法约50步迭代后的IGD值已经跟NS-GA2迭代200步得到的值相当。对于具有不同特征的Pareto前沿的解析函数，优化结果表明本文算法的优化效率明显高于NSGA2。

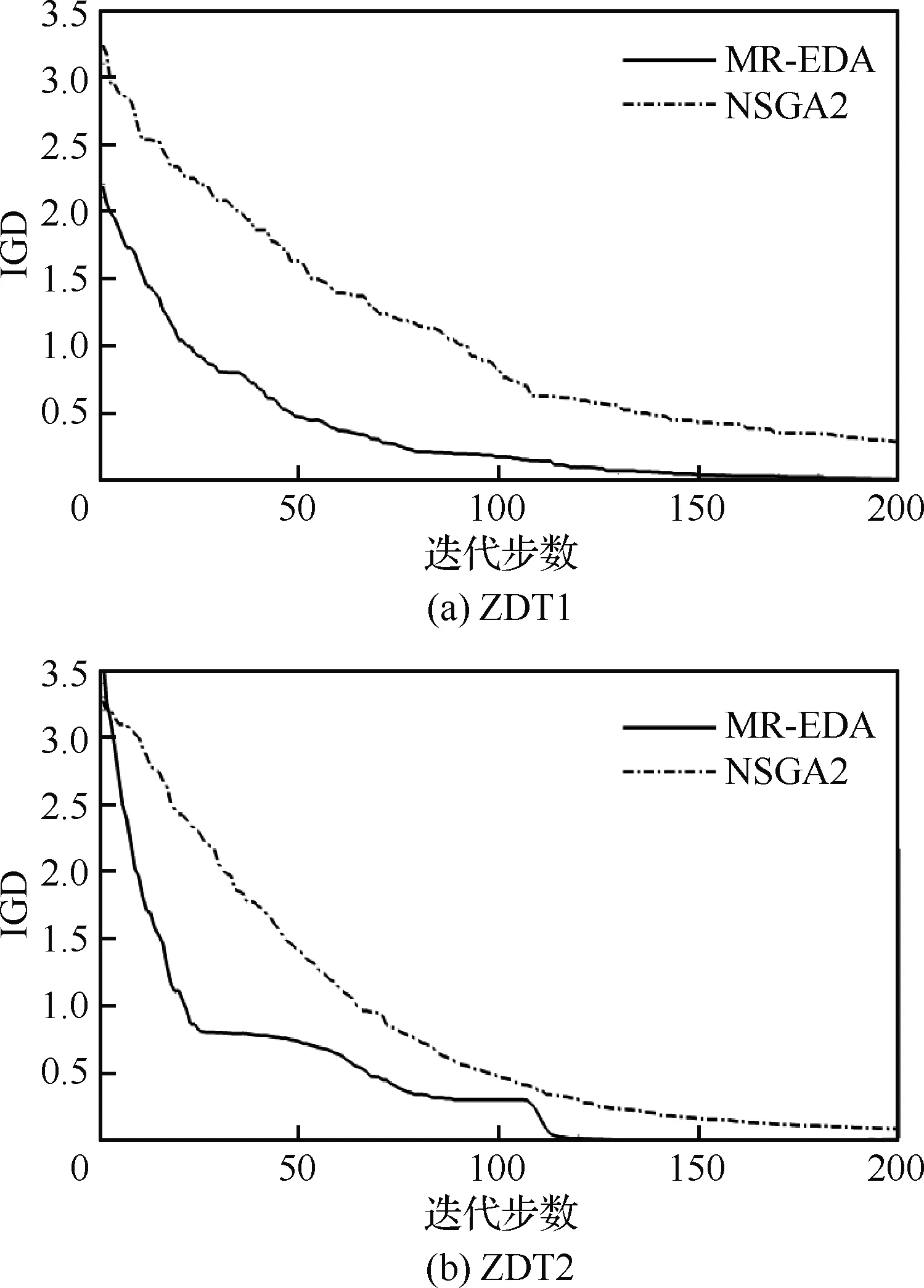
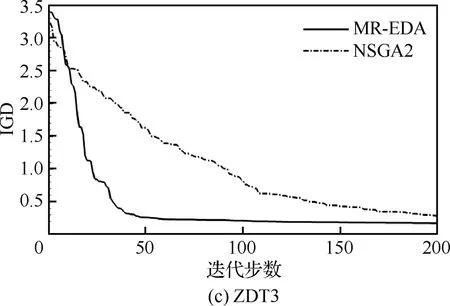
图4 3种测试优化算例的IGD指标收敛过程Fig.4 Convergence histories of IGD obtained by three test optimization examples

3 气动优化算例

选择低雷诺数翼型SD7032为基准进行多目标气动优化设计。翼型参数化采用CST (Class function/Shape function Transformation)方法[24]，翼型上下表面型函数阶数均取为5，类函数指数N1=0.5，N2=1.0，设计变量数目为12。以SD7032的CST参数为基准，设计变量变化范围为±30%。分别考虑2目标和3目标的翼型优化设计问题，其中2目标优化设计问题定义为

(8)

施加力矩系数约束为-0.12≤Cm1≤-0.09，-0.12≤Cm2≤-0.09，并约束翼型最大厚度tmax≥9.0%，其中下标1、2分别表示设计状态1与设计状态2的气动参数。约束采用罚函数方式处理。3目标优化问题在2目标优化问题基础上增加1个设计点，定义为

(9)

采用与2目标问题相同方式处理约束。翼型气动性能求解采用XFOIL，XFOIL在低速低雷诺数范围内能较精确高效预测翼型气动特性[25]。

同样分别利用MR-EDA和NSGA2算法进行优化。对于2目标优化，NSGA2初始种群数目N=100，最大迭代步数设为100，交叉概率0.8，变异概率0.3。MR-EDA中流形重构种群数目N1=N/2，其余参数与NSGA2一致。3目标优化问题种群数目增加为300，其余参数不变。

图5给出了低雷诺数翼型的2目标优化Pareto前沿的收敛过程，其中图5(a)、图5(b)分别给出了MR-EDA、NSGA2的Pareto前沿收敛过程，图中的迭代步数均为5、10、20、100。从图中可以看出，仅迭代5步，本文所提MR-EDA得到的Pareto前沿已经形成了较为规则的分布，在之后的迭代中，Pareto前沿分布更加趋向于规则分布。迭代20步与迭代100步的Pareto前沿基本重合，说明了该算法具有很高的收敛效率。作为对比，NSGA2收敛更为缓慢，在相同的迭代步数下，Pareto前沿收敛性稍差。尽管本文算法最大迭代步数设置为100，但实际上由于算法的收敛效率高，在经过约20步的迭代后，Pareto前沿几乎与NSGA2迭代100步得到的最优Pareto前沿几乎重合。

图5 2目标翼型优化Pareto前沿收敛过程Fig.5 Convergence histories of Pareto front of 2-objective airfoil optimization

图6(a)给出了3目标优化迭代20步时的Pareto前沿。从图中可以明显看出，MR-EDA的收敛速度明显快于NSGA2。迭代100步得到的Pareto前沿在图6(b)中给出，2种算法都已经收敛到相当的水平。分别对比图6(a)和图6(b) 中的Pareto前沿，对于MR-EDA迭代20步的解与迭代100步的解已经十分接近，即本文算法减少了约80%的计算量，说明了本文算法具有高效收敛的特点。

选取3目标优化最优Pareto解集中的一个翼型进行气动性能分析，所选翼型在雷诺数为3.6×105时的功率因子约为117。图7给出了该优化翼型与SD7032翼型的形状。优化后的翼型前缘半径减小，前半部分厚度减小而后半部分厚度增大，上表面曲率过渡更平缓。优化翼型厚度约为9.13%，在约束范围内。图8给出了该翼型在设计点2处的压力分布，并与SD7032翼型的压力分布进行了比较。从图中看出，优化后的翼型转捩点后移，在后半段负压幅值更高，这就使得升力增加，同时低头力矩增大。

表2给出了优化翼型与SD7032在3个设计点的气动性能。从表中看出，优化翼型的升力系数在3个设计点下都有所提升，增加约8%，同时阻力均有所减小。功率因子在3个设计点分别增加了约20.2%、31.7%、27.8%，优化效果明显。力矩系数的在设计点均明显减小，但未超出约束范围。图9给出了该优化翼型与SD7032翼型功率因子随雷诺数变化的关系。从图中可以看出在整个优化区间内，功率因子均有明显提升，这就保证了翼型性能在一定速度范围内平缓过渡。

图6 3目标翼型优化得到的最优Pareto前沿Fig.6 Pareto front of 3-objective optimal airfoil design problems

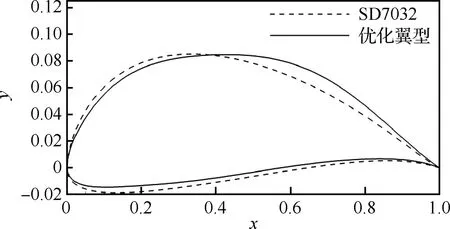
图7 3目标优化得到的Pareto解集中的翼型形状与SD7032翼型Fig.7 Optimal airfoil shape in Pereto set obtained by 3-objective design and SD7032 airfoil

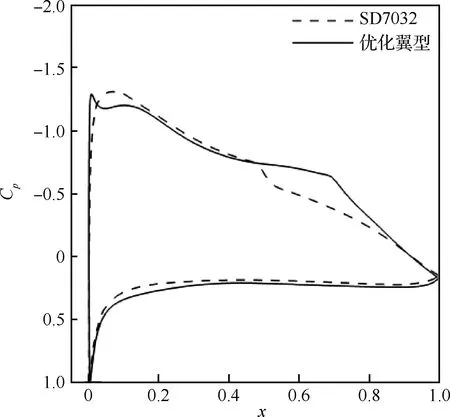
图8 3目标优化得到的Pareto最优解压力分布与SD7032翼型压力分布(Re=3.6×105, α=4°)Fig.8 Pressure coefficient optimal airfoil in Pereto set obtained by 3-objective optimal and SD7032 airfoil (Re=3.6×105, α=4°)

表2 优化翼型与SD7032气动性能比较Table 2 Aerodynamic performance of optimal airfoil and SD7032 airfoil

图9 3目标优化得到的Pareto最优解与SD7032的翼型功率因子随Re变化曲线(α=4°)Fig.9 Variation curves of PI with Re for optimal airfoil in Pareto set obtained by 3-objective design and SD7032 airfoil (α=4°)

4 结 论

本文提出了一种采用流形结构重建的分布估计方法，应用于多目标优化算法。通过解析函数及翼型气动多目标优化算例，验证的本文方法的高效收敛特性，有以下结论：

1) 本文算法充分利用了目标函数空间Pareto前沿的流形结构，以此建立了解集的分布概率模型，用于指导算法演化，避免了传统进化算法盲目交叉变异的缺点，显著提升了优化效率。

2) 通过解析函数算例及2目标、3目标气动优化算例，比较了NSGA2与本文所提算法。结果表明本文算法收敛更快，其中翼型3目标优化设计能够减小约80%的计算量。

3) 流形结构信息能够很好地指导算法演化，充分利用流形结构信息能够极大提高多目标设计问题的优化效率。