基于改进DQN的复合模式在轨服务资源分配

刘冰雁，叶雄兵，周赤非，刘必鎏

1. 军事科学院，北京 100091 2. 中国人民解放军32032部队，北京 100094

随着空间碎片清理、在轨加注等在轨服务技术的不断应用，有限的航天器资源与日益增长的在轨服务需求之间矛盾日益突出。当前，“一对多”服务模式已是国内外主要方式，为了提升任务完成效果与成功概率，“多对一”模式也多被采用[1-2]。“一对多”“多对一”混合共存的服务模式将成为在轨服务的主流。因此，突破传统单一分配原则，最大限度地实现资源最少投入与服务效果最大化，是当前在轨服务资源分配急需解决的重点问题。

任务执行前的在轨资源分配问题本质上是多目标非线性组合优化决策问题，属于多项式复杂程度的非确定性(NP)难题。常用求解方法主要有整数规划、拍卖机制、遗传算法和蚁群算法等。例如，文献[3-4]对“一对多”模式的航天器在轨加注服务分配问题进行了研究，以轨道转移燃耗为优化目标，采用遗传算法进行求解。文献[5]将空间燃料站技术与“一对多”在轨加注问题相结合，构建了一种基于燃料站的可往返式在轨加注分配模型，并用遗传算法求解。文献[6]为实现“一对一”自主式在轨服务，以服务效能、燃料消耗、燃料消耗均衡性为指标，对在轨服务飞行器目标分配问题进行了研究。通常，这些方法由于算法限制只能分别处理“一对多”和“多对一”决策问题[7]，对复合服务模式下的资源分配问题适用性相对较差。

当前，新一代人工智能方法依靠其在自主训练、自我优化方面的优势，处理组合优化决策问题不受服务模式限制，在军事、计算机、通信和交通等领域广泛运用，并取得了显著成效。文献[8]将电磁干扰信道分配问题建模为一个马尔科夫决策过程，运用强化学习算法进行求解，相较传统方法收敛速度更快、方法更智能。文献[9]针对蜂窝网资源分配多目标优化问题，基于深度强化学习提出了一种蜂窝网资源分配方法，在传输速率和系统能耗优化方面明显优于传统方法。文献[10]针对传统的流水车间资源分配方法数据利用率低、实时性较差等不足，利用神经网络和强化学习实时性、灵活性优势进行改进，使新方法能够在更小的迭代次数内获得较优解。

本文依据在轨服务的复合服务模式需求，在任务执行前，综合考虑服务对象重要性、资源投入综合效益以及总体能耗估计，基于对DQN(Deep Q-Network)收敛性和稳定性的改进，提出了在轨服务资源分配方法。该方法在建立资源分配模型的基础上，构建资源分配双向训练网络，即以综合效益为优化目标进行前向传输、能耗效率作为奖惩值进行反向训练，是目前能够满足复合服务模式下资源分配需求的有效方法。该方法自主性强、收敛速度快，在分配效益和总体能耗的优化方面具有明显优势，能够更有效地解决多目标非线性组合优化问题。

1 复合服务模式的在轨资源分配模型

在轨服务的复合模式，是针对众多不同类型、不同重要程度的服务对象，综合考虑航天器投入及效益，采取普通对象“一对多”、重要对象“多对一”分配策略的一种混合服务模式。相较单一服务模式，此种方式需要同时兼顾航天器投入量和各类对象服务效果，对分配模型的综合决策能力要求高，通常还需人工辅助。本文借鉴先期毁伤准则[11-12]和能量效率思维[13-14]，提出了一种满足此类复合服务模式的资源自主分配模型。

假设m∈{1,2,…,M}表示能够提供在轨服务的第m个航天器，n∈{1,2,…,N}表示在轨服务的第n个对象，Lm,n表示航天器m与服务对象n之间的资源分配关系，若航天器m服务对象n，则Lm,n=1，反之Lm,n=0。令Wn为第n个对象的重要程度。针对不同重要程度的服务对象，兼顾服务成功概率和燃料消耗，通过自主分配航天器，以达到既节省航天器投入又满足期望效果。资源分配综合效益可表示为

(1)

式中：G为航天器分配的综合效益；Dm,n为任务执行前，对航天器m服务对象n的燃料估计量，是对此次任务执行成本的一种考量，其值可根据该航天器与服务对象的轨道根数，基于当前环境选取最优轨道转移方式，通过机动推进剂消耗模型和服务过程燃料消耗模型计算获得[15-17]。

用服务对象同时受多个航天器服务的燃料估计量以及服务成功概率来综合衡量系统能耗，则资源分配的总体能耗效率可以表示为

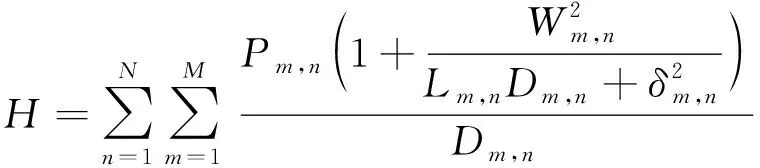
(2)

根据资源分配目标，在满足预期服务成功率约束的条件下，需要求解的多目标非线性组合优化决策问题描述为

(3)

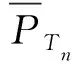
2 方法介绍

本文除了考虑资源分配综合效益外，还综合考量能耗效率，于是复合服务模式下的在轨资源分配问题便成了NP-hard问题，难以求得最优解。当前常用方式是将该问题转化为次最优解求解，但这类求解的复杂度高，影响模型运行效率[7]，本文对经典DQN方法进行了收敛性和稳定性改进，并基于此求解该问题。

2.1 经典DQN方法改进

针对在轨服务资源分配智能化需求，弥补经典DQN方法存在奖励偏见和过估计的问题[18]，进行了方法适应性改进，以提升方法的收敛性和稳定性。

2.1.1 DQN的收敛性改进

为大幅提升神经网络训练效果，加快收敛速度，采用一种竞争网络取代经典方法中的单输出网络模型[19]。行为值函数Q(St,a)可自然拆分为状态值函数V(St)和行为优势函数A(St,a)2部分。其中，状态值函数与行为无关；动作优势函数与行为相关，为行为相对状态的平均回报的好坏程度，可用以解决奖励偏见问题。据此，将经典神经网络方法的全连接层分为一个输出状态函数V(St)和一个输出行为优势函数A(St,a)，最后再通过全连接合并成行为状态Q(St,a)，即

Q(St,a)=V(St)+A(St,a)

(4)

状态值函数被拆分后，当行为优势值一定时，状态值和行为优势值有无穷种可行组合，而事实上只有小部分的组合是合乎情理的。为此，利用行为优势函数A(St,a)期望值为0这一特性[19]，对行为优势函数A(St,a)加以限制，将式(4)修改为

Q(St,a)=V(St)+

(5)

这样，用行为优势函数减去当前状态下所有A(St,a′)的均值，使行为优势函数的期望值保持为0，进而确保模型快速收敛且输出高效。

2.1.2 DQN的稳定性改进

深度强化学习的目标是找到最优的策略，但过估计量的非均匀出现，致使值函数的过估计影响决策，从而导致最终的决策并非最优，而只是次优。采用Q-learning学习机制的行为选择中，通过值函数更新，时间差分(TD)方法的目标为[20]

(6)

式中：Rt+1为状态St+1的奖惩值；γ∈[0,1]为折扣因子；Q(St+1,a;θt)为采用行为a和参数θt时，神经网络对状态St+1价值的预测。

选出状态St+1的最佳行为a*后，DQN方法是利用同一个参数θt来选择和评估行为。为了削弱最大误差的影响，在此引入另一个神经网络，分别用不同的值函数选择和评估行为[21-22]。由此，利用参数θt通过式(6)进行行为选择，在选出最佳行为a*后，运用另一个神经网络的参数θ′t进行行为评估:

(7)

将这一思路运用到强化学习中，修改得到新的TD目标式为[23]

(8)

2.2 在轨服务资源分配的智能方法

基于改进的DQN方法，发挥强化学习试错自主学习优势，运用神经网络前向传输和反向训练特性，求解在轨资源分配的多目标非线性组合优化决策问题。

2.2.1 前向传输优化目标

在前向传输过程中，在追求资源分配高效益的同时，为确保各对象要有航天器服务且均能达到预设服务成功概率门限，结合式(3)，将资源分配综合效益最优化问题表示为

(9)

采用惩罚函数法将约束优化问题转换为如下无约束优化问题

(10)

式中：参数δ为惩罚系数；hn、gn和Dn的表达式分别为

(11)

2.2.2 反向训练奖惩值

在反向训练过程中，依据式(5)和式(8)，构建损失函数：

(12)

其中，将资源分配的总体能耗效率作为奖惩值，即

(13)

为了有效解决强化学习中的探索与利用问题，即持续使用当前最优策略保持高回报的同时，敢于尝试一些新的行为以求更大地奖励，则依据探索率ε采取ε-greedy贪婪策略：

π(a|St)=

(14)

2.2.3 资源分配网络架构

整个网络架构由训练、误差、Q现实、Q估计以及行为选择等模块组成，借助TensorFlow展现改进的深度强化学习网络，如图1所示。图中：S为当前状态；S_为下一步状态；Value为价值函数；Advantage为优势函数；l1为神经网络；eval_net为估计网络；target_net为目标网络；Q_target为目标Q函数；loss为损失函数；Assign[0-5]为分配；Train为训练网络；DuelDoubleDQN为DQN收敛性和稳定性改进网络。

图1 DQN收敛性和稳定性改进的网络结构TensorFlow表示Fig.1 Network structure on DQN convergence and stability improvement by TensorFlow representation

2.2.4 DQN综合改进方法的流程

在明确网络输入、输出、关键模型和训练结构后，综合DQN稳定性改进与收敛性改进，给出智能方法的主体流程：

步骤1 利用随机θ初始化行为值Q。

步骤2 令θt=θ，根据式(4)和式(5)计算TD目标的行为值Q。

步骤3 循环每次事件。

步骤4 初始化事件的第一个状态，通过式(1) 预处理得到当前资源分配综合效益。

步骤5 循环每个事件的每一步。

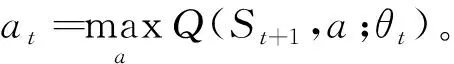
步骤7 仿真器中执行行为at，观测回报Rt。

步骤8 设置St+1=St，整合(St,at,Rt,St+1)并存储在回放记忆Memory中。

步骤9 从Memory中均匀随机采样一个转换样本数据，用(St,at,Rt,St+1)存储结果表示。

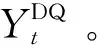
步骤12 如果St+1是终止状态，当前轮迭代完毕，否则转到步骤5。

3 算例求解与分析

为验证本文构建的复合服务模式下的在轨资源分配模型的适用性，以及DQN收敛性和稳定性改进方法求解该在轨资源分配问题的有效性和优越性，进行了算例仿真。

3.1 问题描述

假设在某次在轨加注任务中，有9颗重要程度Wn=0.6(n=1,2,…,9)、1颗W10=0.9的ECO卫星等待加注燃料，其轨道根数[24]如表1所示。表中：e为离心率；i为轨道倾角；Ω为升交点黄道经度；ω为近心点角；τ为平近点角。现有3架位于轨道半径39 164 km、初始真近点角0°、推进系统比冲300 s的航天器可开展在轨加注服务。航天器拟采用多圈Lambert轨道转移方式，结合轨道根数确定到各目标轨位的速度增量，结合齐奥尔科夫斯基公式估算得到燃料消耗量D[25-26]。现已知各航天器对卫星的服务成功概率P。

D=

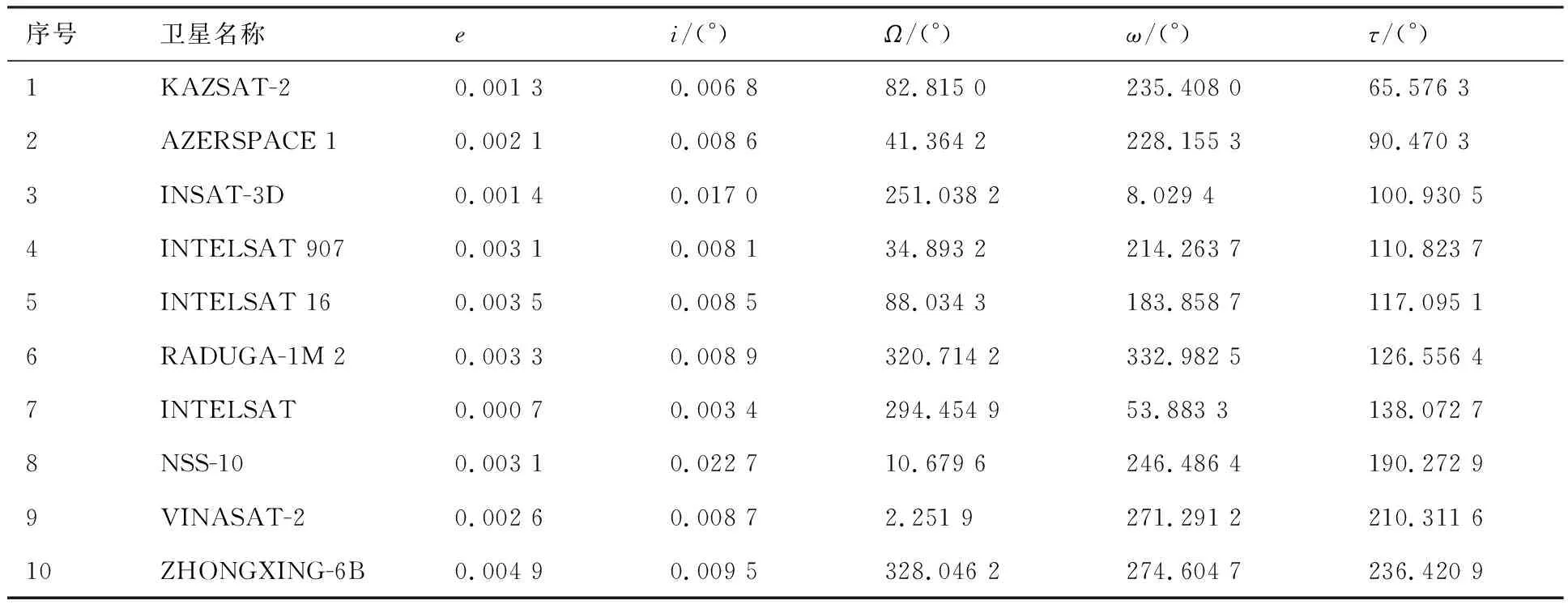
表1 GEO卫星的轨道根数[24]Table 1 Orbit elements of GEO satellite[24]

任务要求在满足70%服务成功概率的基础上，提升对10号卫星的服务成功概率并达到85%。由此，决定采取“1对9”和“2对1”的复合服务模式。

3.2 方法对比

为解决该资源分配问题，本文试图借鉴在轨服务资源分配相关研究成果[4-6,25-28]进行求解，但发现这些方法只能单独解决“一对多”或“一对一”服务模式的资源分配问题，不适合本文涉及的复合服务模式。为了对比分析不同方法的运算耗时情况，只考虑算例中的“一对多”在轨服务资源分配问题，分别用3种方法进行求解。

仿真运算依托1.6 GHz、1.8 GHz双核CPU、8 G RAM计算硬件，运用python语言PyCharm编译环境进行，各方法的耗时情况如图2所示。其中，蚁群算法运用全局搜索方式计算开销较大，不同的起始方向导致运算时间波动大，平均耗时0.32 s；遗传算法没能够利用反馈信息训练时间相对较长，随机交叉变异致使运算时间波动较大，平均耗时0.19 s；改进DQN方法运用神经网络自主训练时间最短，探索与利用策略的使用致使运算时间有小范围波动，平均耗时0.06 s。因此，本文所提方法充分发挥神经网络前向传输和反向训练的运算优势，利用强化学习试错奖励的决策机制，相比较运算效率更高，也更适合本文所涉及的复合模式下的在轨资源分配问题。

图2 3种方法的运算耗时对比Fig.2 Operation time comparison between three method

3.3 求解分析

针对复合模式下的在轨服务资源分配问题，根据问题描述，运用本文提出的基于DQN收敛性和稳定性改进的在轨服务资源分配方法，通过网络自主训练、自主决策可获得最优资源分配策略，即由航天器2和3共同对卫星10进行加注，其他卫星由航天器1提供服务。

如表2所示，以全0矩阵初始化资源分配状态①，代入在轨资源分配模型，此时无资源投入，不符合任务要求，进而通过改进的深度强化学习网络自主学习。训练过程中，状态②资源投入较节省，但不符合服务模式要求；状态③高资源投入使得能耗效率低，综合效益达到最低值；状态④符合各项约束，但综合效益值非最大。通过多次自主学习、多轮迭代后，方法收敛至状态⑤，所提供策略即满足各项服务要素，又实现综合效益最大化，是该任务的最优资源分配策略。

与此同时，运用经典DQN方法进行求解，获得了相同结果，侧面印证了结果的准确性。2种方法的误差函数值对比如图3所示，改进DQN方法对全连接层的区分处理方式，促使仅学习70次便可实现误差0.01的训练效果，整个训练过程的误差函数值也以快近一倍的速率下降，在收敛性方面的改进效果明显。2种方法的奖惩值对比如图4所示，改进DQN方法在行为估计时引入另一神经网络，确保奖惩值在快速上升的同时波动更小，自主学习仅33次后便可保持在0.197 8最佳奖惩值附近，充分体现了稳定性方面的改进优势。

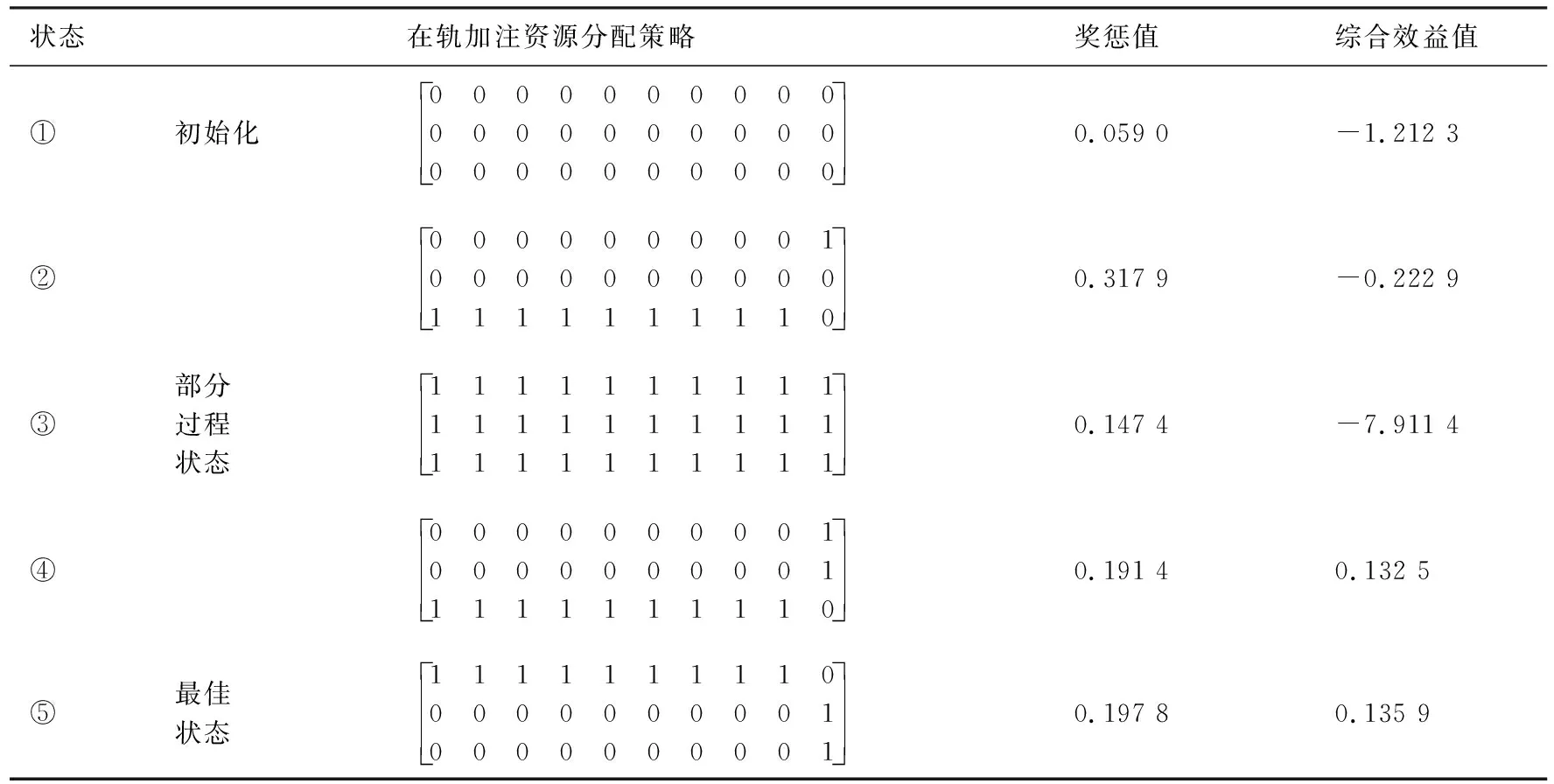
表2 基于改进深度学习的在轨加注资源分配策略Table 2 An on-orbit injection resource allocation strategy based on improved deep learning

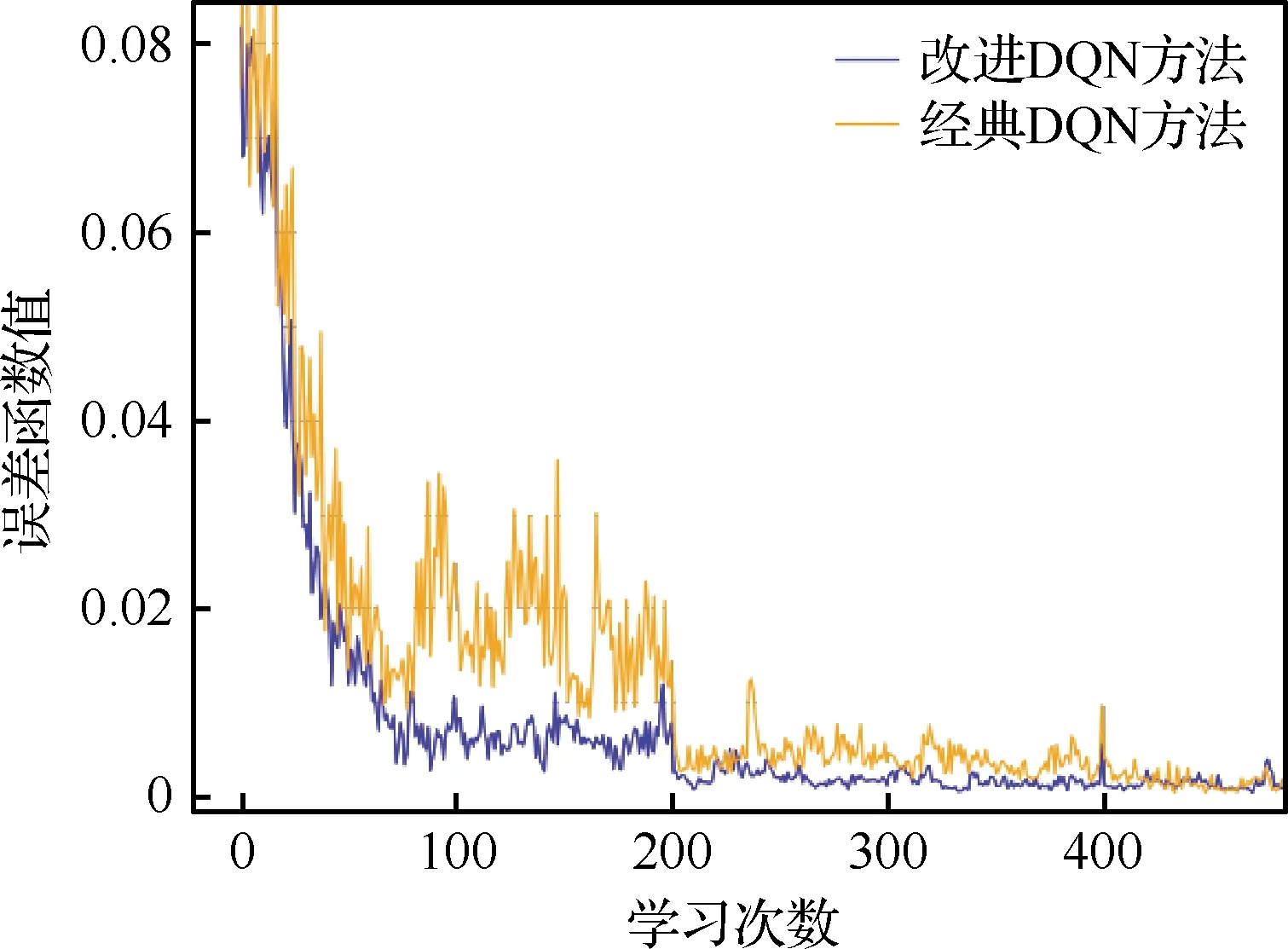
图3 2种方法的误差函数值对比Fig.3 Error function value comparison between two method

图4 2种方法的奖惩值对比Fig.4 Rewards comparison between two method

4 结 论

1) 构建了复合服务模式下的在轨资源分配模型。针对在轨服务多样化模式需求，为弥补当前资源分配模型应对复合任务的不足，同时考虑重要性、效益以及能耗因素，研究了在轨服务资源分配问题。

2) 进行了DQN方法的收敛性和稳定性改进。针对在轨服务资源分配问题特性，弥补经典方法奖励偏见和过估计问题，改进DQN方法，提升了方法敛性和稳定性。

3) 提出了基于DQN收敛性和稳定性改进的在轨服务资源分配方法。区分服务对象重要程度，在提高资源分配综合效益的同时，尽可能地增大总体能耗效率，有效解决了多目标非线性组合优化决策问题，同时对于解决其他领域资源分配问题具有较强的借鉴意义。