价格与替代效应对农业生产中化肥施用的影响——以玉米和圆白菜为例

尹 峻 党敬淇 孙小霞*

(1.福建农林大学 可持续发展研究所,福州 350002； 2.浙江大学 管理学院,杭州 310058)

农业为人类的衣食之源、生存之本、发展之基，保障其平稳健康发展是关系国计民生的重大任务。世界各国农业发展历史与现实表明，施用化肥是现代农业增产效率最高且效果最显著的重要方式[1-2]，对中国农业生产发展做出了极为重要的贡献[3]。得益于化肥的使用，中国以仅占世界耕地总面积7%的土地，为约占世界总人口18%的13亿人提供粮食。如图1所示，2001—2015年中国粮食产量和化肥投入量之间呈较强的正相关性，相关研究进一步指出，化肥施用量的增加显著促进了中国粮食单产提高，帮助中国2004—2012年粮食生产实现“九连增”[4]。尽管化肥投入是保障农业增产的重要因素之一，但中国化肥投入近年来已远超国际标准。2014年中国的化肥投入量已经接近6 000万t，超过亚洲化肥投入总量的一半(52.75%)，占同年世界化肥投入总量的30.91%，位居世界第一(见表1)，平均化肥施用强度达到了565.3 kg/hm2，约为亚洲平均化肥施用强度的2.5倍，为世界平均化肥施用强度的4.1倍，远远超出安全施肥国际标准(225 kg/hm2)上限。

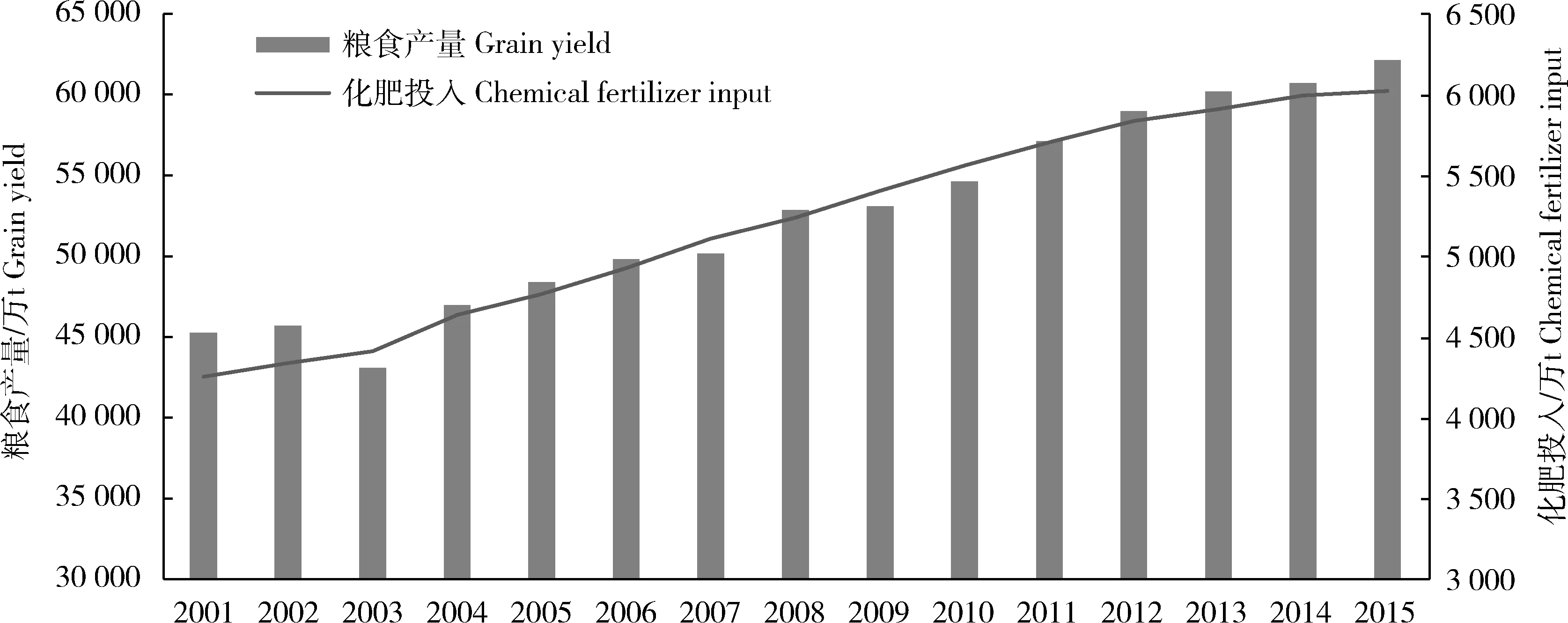
图1 2001—2015年中国粮食产量和化肥投入量[5-6]
Fig.1 2001-2015 China’s grain output and fertilizer input[5-6]

表1 2014年部分国家和地区化肥投入情况
Table 1 Fertilizer input in some countries and regions in 2014

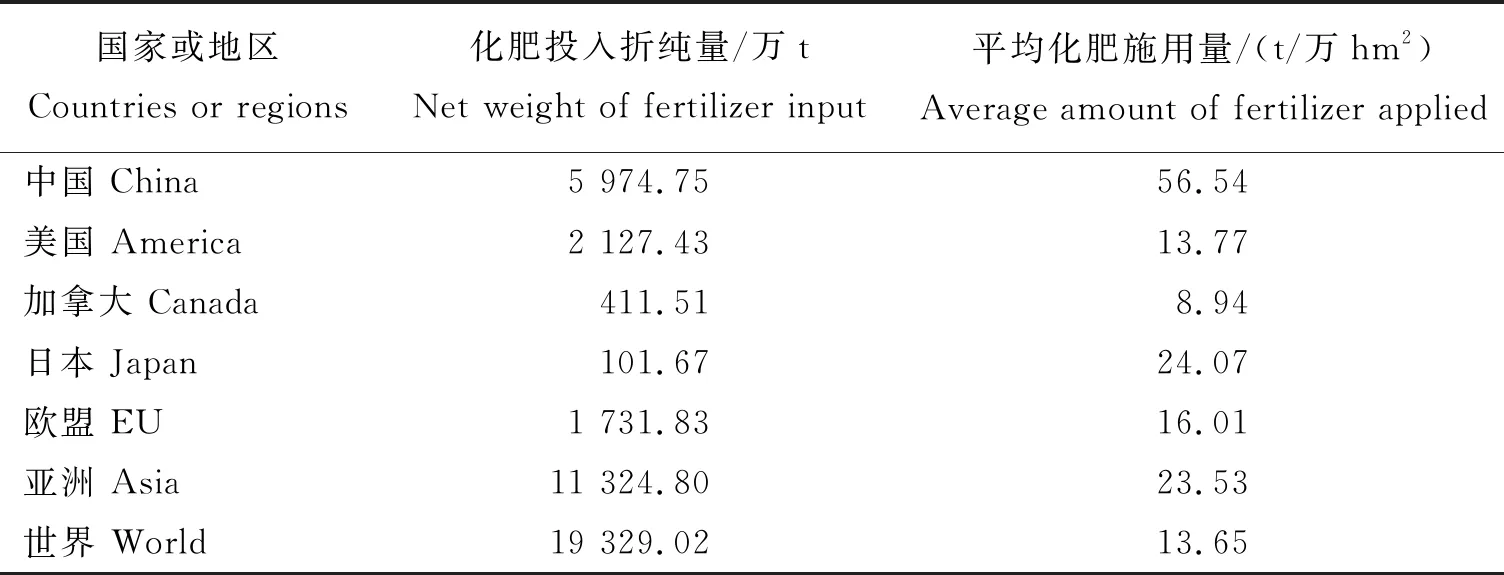
国家或地区Countries or regions化肥投入折纯量/万tNet weight of fertilizer input平均化肥施用量/(t/万hm2)Average amount of fertilizer applied中国 China5 974.7556.54美国 America2 127.4313.77加拿大 Canada411.518.94日本 Japan101.6724.07欧盟 EU1 731.8316.01亚洲 Asia11 324.8023.53世界 World19 329.0213.65

注：资料来源：联合国粮食及农业组织数据库 http:∥www.fao.org/faostat/en/。

Note： Data sources: Food and Agriculture Organization of the United Nations， http:∥www.fao.org/faostat/en/.

已有研究表明，近年来中国普遍存在的施肥过量、偏施肥和化肥利用率偏低等问题，已造成了严重的农业面源污染并导致农业土壤、江河湖泊和大气环境质量衰退[7-11](1)2010年2月6日环保部等三部委公布的《第一次全国污染源普查公报》显示，中国种植业氮、磷排放量分别为159.78万t和10.87万t，分别占总排放量的33.8%和25.7%。。这些问题引起了党和国家的

高度重视：2015年，农业部出台《到2020年化肥使用量零增长行动方案》指出“即使化肥使用量保持平稳水平，仍然远远高于国际安全施肥标准”，强调推进化肥减施势在必行；2017年，中央一号文件提出落实农业清洁生产，深入推进化肥农药零增长行动，促进农业节本增效；党的十九大报告再次强调“加强农业面源污染防治”，进一步促进化肥减施和高效利用。上述一系列政策主张均表明，倡导化肥高效施用、推动农业生产绿色增长已经成为当前中国农业发展的重要主题[12]。因此，结合当前政策导向和研究现状，考察化肥投入的影响因素具有重要的理论与现实意义。

目前，国内外关于化肥投入的研究主要集中于考察各类社会因素与农户特征因素对农户施肥行为的影响，基于发展中国家和地区的微观数据进行研究，分析农户是否施用化肥和化肥投入量的决定因素等问题[13-19]，以及化肥过量施用的原因等问题[11,20-22]，但是缺乏对价格这一重要经济因素的系统考察，多数研究仅关注化肥与产出价格而较少涉及其他价格变量。此外，虽然国外已有关于化肥与其他农业生产要素之间替代关系研究，但多局限于早期发达国家[23-25]，而国内研究则缺乏涉及化肥投入的讨论[26-28]，因此研究化肥与其他农业生产要素之间替代关系，尤其是在当前普遍存在过量施肥情境下，对于中国农业绿色、高效和集约化生产具有更加重要的政策价值。

基于上述文献分析和经验事实，通过构造超越对数成本函数和影子替代弹性，利用2004—2016年中国主要玉米和圆白菜产区的化肥及其他要素投入与价格数据，采用似不相关回归方法进行实证分析，考察玉米和圆白菜生产中化肥的需求价格弹性，化肥和劳动的替代弹性以及化肥和机械的替代弹性，为政府制定或调整化肥政策提供建议，以期推动农业生产中化肥合理高效施用，促进农业面源污染治理和农业生产的可持续发展。

1 理论分析框架

微观经济学生产理论表明，生产要素的需求同时受到要素自身价格和其他要素价格的影响。要素需求对自身价格变动的反应程度即要素的需求价格弹性(Demand price elasticity)，表示为要素需求量变化的百分比与要素自身价格变化的百分比的比值[23,29]：当要素的需求变动大于价格变动时，需求价格弹性为富有弹性或高弹性，反之则为缺乏弹性或低弹性。给定产出水平，要素需求对其他投入要素价格变动的反应程度即要素之间的替代弹性(Elasticity of substitution)，表示为要素需求量变化的百分比与其他要素价格变化的百分比的比值[23,30]：若要素A价格下降时，会激励生产者增加要素B的投入，则要素A与B之间呈现互补关系，反之则要素A与B之间呈现替代关系。

化肥作为农业生产中一种重要的要素投入，其需求在生产决策中与农户面临的化肥、劳动力与机械价格等息息相关[27,31-33]：

1)化肥市场价格的变动将会导致农户化肥投入的反方向变动，且这一变动幅度取决于化肥的需求价格弹性。若化肥需求富有弹性，则化肥投入量将很大程度上取决于化肥的市场价格，政府可以通过调整化肥补贴等价格政策对农户化肥投入进行干预，以实现化肥的合理有效施用。若化肥需求缺乏弹性，则化肥市场价格的变动将无法导致农户化肥投入的较大变化，通过价格政策限制农户过量施肥将不再奏效。

2)化肥与劳动之间的替代关系会显著影响农户的化肥施用决策，但这一替代关系较为复杂：一方面，中国主要靠人工施肥，化肥投入需要借助劳动力辅助，两者之间可能呈现互补关系，即劳动力价格上涨会通过减少农业生产中的劳动力需求进而降低化肥投入量，此时政府可以通过农业技术培训、鼓励外出打工等政策调整农业生产中的化肥施用量；另一方面，劳动力价格上涨将导致农户疏于田间管理，并通过“少次多量”增施化肥来保证产量，这可以理解为两者之间呈现替代关系，此时政府则需要提供农业生产补贴、多样化经营等政策适当降低劳动力价格以调整农业生产中的化肥施用量。

3)化肥与机械之间的替代关系也会显著影响农户的化肥施用决策，这一替代关系同样较为复杂：一方面，近年来中国农业生产水、肥、药、机一体化迅速发展，作物大量通过农业机械进行施肥，使得两者之间可能呈现互补关系，即机械价格上涨会降低化肥投入量，此时政府可以通过减少农机补贴、增加培训和推广精细作业等政策调整农业生产中的化肥施用量；另一方面，部分农业机械的使用可以有效促进化肥在土壤中的溶解和吸收效率，达到保证产量前提下减少化肥施用的效果，因此可以理解为两者之间呈现替代关系，此时政府可以通过增加农机补贴、适度规模经营等政策调整农业生产中的化肥施用量。

综上所述，化肥的需求价格弹性、化肥与劳动力和机械之间的替代弹性在很大程度上影响了农业生产中的化肥施用量，对于政府推进合理施肥、优化农业生产要素配置和促进农业高质量发展具有较强的政策指导意义。然而现阶段化肥的需求价格弹性数值大小，以及化肥—劳动和化肥—机械之间是互补还是替代关系，均无法通过理论分析得出一致的结论，需要利用数量分析工具作进一步实证研究。

2 数量模型构建

为系统考察中国农业生产中化肥的需求价格弹性及化肥与其他要素投入之间的替代弹性，本研究采用超越对数成本函数(Translog cost function)作为基本框架构造模型，并基于此推导替代弹性公式。超越对数函数属于结构上的平方响应面(Quadratic response surface)模型，具有易估计和包容性强优势：在单要素与多要素情形下函数形式均不变；不依赖于其本身的非线性结构，可直接利用线性模型进行估计；毋需针对特定参数施加先验假设，估计更贴近真实生产情况等[34-36]。相较于超越对数生产函数，超越对数成本函数将要素价格视为外生变量，能更有效地刻画农户的生产经营决策，因而被广泛应用在要素替代关系和技术偏向测度、生产前沿分析等方面。

2.1 超越对数成本函数模型

超越对数成本函数是超越对数生产函数的对偶函数，因此可以通过超越对数生产函数推导出来。在多要素情形下，超越对数生产函数的非线性形式可以表示为：

Y=f(X1.X2,…,Xn)

(1)

假定一系列要素价格不变且可获得，在给定产出水平条件下求解成本最小化问题，得到的解集为成本最小化条件下的要素需求集：

xi=xi(X,p)

(2)

相应的成本最小化条件下的总生产成本可由成本函数C(Y,p)=Σipixi表示。在规模报酬不变的假设下，对成本函数两边取对数可以得到：

lnC(X,p)=lnY+lnc(p)

(3)

对式(3)进行二阶泰勒展开：

lnC=γ0+ΣiαilnY+ΣiβilnPij+ 1/2ΣiΣjβijlnPilnPj+ΣiΣjγijlnPilnYj+ξ

(4)

结合郝枫[35]的做法，将产出用各类要素投入代替，可重写式(4)为：

lnC=γ0+ΣiαilnXi+ΣiβilnPi+ 1/2ΣiΣjαijlnXilnXj+ 1/2ΣiΣjβijlnPilnPj+ΣiΣjγijlnPilnYj+ξ

(5)

式(5)是一个超越对数成本函数，其中：C为生产总成本，P为要素价格，X为要素投入量，i,j=1,2,…,n表示不同的要素。根据Shephard引理，对式(5)超越对数成本函数各项求要素价格P的偏导数，可以得到在总成本最小化条件下的要素需求函数，即各要素成本份额(S)方程：

Si=PiXi/C=∂lnC/∂lnPi=βi+ΣiβilnPi+ΣjγijlnXj

(6)

由于生产函数需要包含产出所需要的全部要素投入，因此要素成本份额的总和必须为1，式(5)须满足Σiβi=1且Σiβij=Σjβij=0；同时，可积函数Young定理要求式(5)具有理论上的对称约束βij=βji。Christensen等[37]指出，在缺乏规模报酬不变的假定前提下，超越对数成本函数包含了份额函数所没有的重要参数，在估计时应同时估计份额函数与成本函数。Greene[36]认为成本函数除了提供γ0的估计值外并没有实际意义。此外在实际操作过程中，随着待估计参数的增多，式(5)表示的超越对数成本函数交叉项数量迅速增加，会严重损失自由度并大幅增加解释变量之间的共线性[35]。因此本研究采用式(6)所示的成本份额函数进行估计。

2.2 替代弹性计算公式

目前，常用的替代弹性公式有Allen替代弹性(Allen elasticity of substitution，AES)、Morishima替代弹性(Morishima elasticity of substitution，MES)和影子替代弹性(Shadow elasticity of substitution，SES)。Binswanger[23]提供了基于式(6)参数估计结果的AES计算公式：

(7)

MES刻画了在产出水平和其他要素价格不变的情况下，要素j的价格Pj变化，对要素i的投入Xi相对要素j的投入Xj变化率Xi/Xj的影响[38]：

σijM=Pj[(Cij/Ci)-(Cij/Cj)]= ∂ln(Xi/Xj)/∂lnPj

(8)

SES刻画了在产出水平和其他要素价格不变的情况下，要素j的价格Pj相对于要素i的价格Pi的变化率Pj/Pi，对要素i的投入Xi相对要素j的投入Xj的变化率Xi/Xj的影响[29]：

σijS=(Cii/CiCi+2Cij/CiCj-Cjj/CjCj)/

(1/PiCi+1/PjCj)=∂ln(Xi/Xj)/∂ln(Pj/Pi)

(9)

Binswanger另外给出了要素的需求价格弹性[23]：

Eii=σiiSi=βii/Si+Si-1,i≠jEij=σijSj=βij/Si+Sj,i=j

(10)

根据式(7)～(10)可以推导出基于式(6)参数估计结果的MES和SES计算公式：

σijM=Eij-Ejj=Sj(σij-σjj)

(11)

σijS=[Si/(Si+Sj)](Eij-Ejj)+ [Sj/(Si+Sj)](Eij-Eii)= [SiSj/(Si+Sj)](2σij-σii-σjj)

(12)

比较式(7)、(11)、(12)可以得出，相较于AES和MES，SES更接近Hicks对替代弹性的定义，且估计结果在不同形式的超越对数成本函数模型下均更为稳健[35]。综上所述，本研究采用式(12)所提供的SES方法来估计各农业投入要素之间的替代弹性。

3 数据来源与变量说明

考虑到农业生产作物的代表性和数据的可得性，本研究选择玉米和圆白菜种植所需的化肥等要素投入作为分析对象。玉米是中国的三大主粮之一，同时也是食品、酒精、燃料等行业所需要的重要原材料，在中国的种植基本覆盖了各粮食主产区。据《全国农产品成本收益资料汇编》[39]数据显示，玉米的化肥需求折纯量约为371.34 kg/hm2，是平均需肥量最大的粮食作物，也是中国肥料吸收和利用率相对较低的作物之一[40-41]。圆白菜在中国各地广泛种植，尤其在长江以南主要产区占作物总播种面积的近50%，消费量也居中国各类蔬菜之首，是重要的蔬果类经济作物。圆白菜的化肥需求折纯量约为454.63 kg/hm2，需水和氮肥量均较大，且肥料易流失，偏施肥和过量施肥现象较严重[42]。因此，通过研究玉米和圆白菜的化肥需求价格弹性及与其他要素之间的替代关系在一定程度上对中国农业生产过程中的化肥减施具有较大的参考价值。

本研究数据均来源于《全国农产品成本收益资料汇编》[39]、《中国农村统计年鉴》[6]和《中国统计年鉴》[5]2004—2016年玉米和圆白菜主产区化肥与其他各类生产要素的投入和价格数据，其中玉米主产区覆盖中国20个省，圆白菜主产区覆盖15个省(2)玉米主产区覆盖的20个省份为：河北、山西、内蒙古、辽宁、吉林、黑龙江、江苏、安徽、山东、河南、湖北、广西、重庆、四川、贵州、云南、陕西、甘肃、宁夏和新疆；圆白菜主产区覆盖的15个省份为：天津、河北、内蒙古、吉林、江苏、山东、浙江、上海、福建、湖北、江西、重庆、广西、云南、甘肃和新疆。。根据研究目标以及实证模型对数据的要求，本研究共设置要素投入与要素价格两类指标，涵盖化肥、劳动、机械和其他农业生产要素，各变量详细定义如下：

1)化肥投入与化肥价格。选取包括磷肥、氮肥、钾肥和复合肥在内的单位面积化肥折纯用量(kg)作为化肥投入指标；化肥价格(元/kg)通过化肥成本/化肥投入量得到。化肥折纯量指化肥实际含有氮、磷、钾等养分的质量，通过N、P2O5、K2O等化学元素的质量百分比×化肥实际质量得到，化肥折纯量能够比较准确地反映农业生产中实际需要的化肥数量。

2)劳动力投入与劳动力价格。选用农作物生产中的单位面积用工投入(工日)作为劳动力投入指标；劳动力价格(元/工日)通过单位面积劳动力成本/用工投入得到。《全国农产品成本收益资料汇编》[39]中的用工成本同时包含了家庭用工成本与雇工成本，二者均反映了当期劳动力市场价格；同时，考虑到农业劳动力需求具有季节性特征，单独使用其中任何一种指标都会导致偏误，因此本研究在数据处理过程中对家庭用工投入和工价、雇工投入与工价进行了加权平均。

3)机械投入与机械价格。《全国农产品成本收益资料汇编》[39]仅提供了单位面积机械作业费用，未提供具体的机械投入数量信息，故本研究参考陈书章等[43]的方法，将扣除水费、畜力费等非机械费用的租赁作业费作为机械投入量(元)，并通过机械化农具价格指数和半机械农具价格指数加权平均得到机械价格。

4)其他要素投入与其他要素价格。其他要素投入为总生产成本扣除化肥、劳动力和机械的其他成本，包括种子、农膜、农药、土地、燃料动力费、管理费、固定资产折旧等成本；其他要素投入内容复杂且缺乏具体的投入数量数据，因此本研究中的其他要素价格用农业生产资料综合价格指数进行替代。

上述各变量的描述性统计结果报告在表2中。

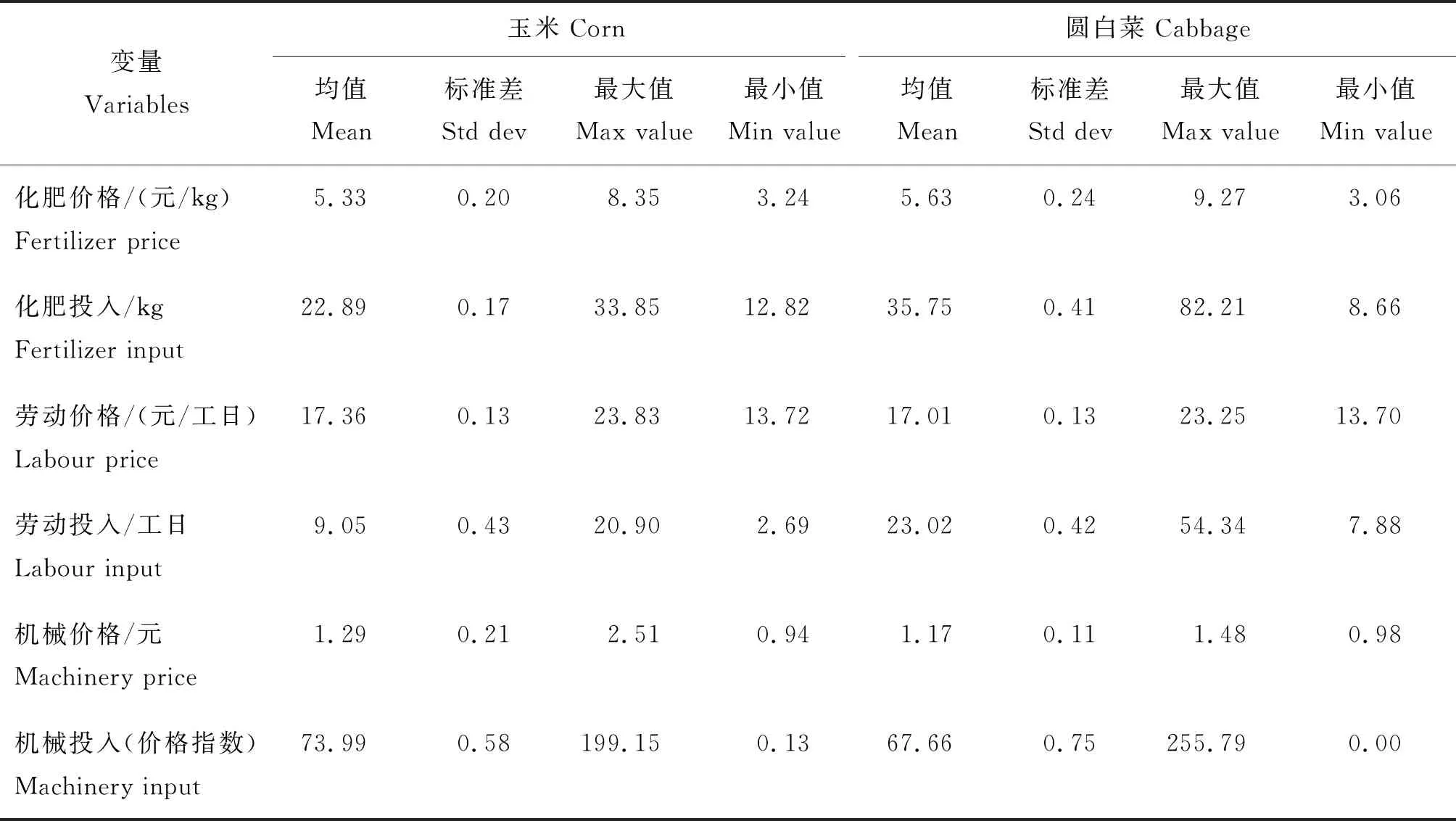
表2 主要变量描述性统计Table 2 Descriptive statistics of main variables

4 实证分析

本节主要包含三部分内容：第一部分通过上述提供的超越对数成本份额函数构造玉米和圆白菜的计量回归方程，利用2004—2016年化肥及其他农业生产要素的省级数据，分别估计中国玉米和圆白菜的成本份额系数；第二部分基于回归估计结果计算中国玉米和圆白菜生产中化肥的需求价格弹性；第三部分则进一步计算玉米和圆白菜生产中化肥与其他农业生产要素之间的替代弹性。

4.1 玉米和圆白菜成本份额函数估计结果

根据式(6)分别构造玉米和圆白菜的超越对数成本份额回归方程如下：

Siktcorn=βi+ΣjβijlnPjkt+ΣjγijlnXikt+Σ112γitTt+Σ119αitDk+εikt

(13)

Siktcabb=βi+ΣjβijlnPjkt+ΣjγijlnXikt+Σ112γitTt+Σ115αitDk+εikt

(14)

回归方程组(13)和(14)中S、P、X各变量定义与前述相同，Tt为时间虚拟变量，Dk为省份虚拟变量，i、j分别代表不同的农业生产要素，t代表时间，k代表省份。由于需要估计不同作物在不同农业生产要素投入下的成本份额系数，本研究采用似不相关回归(Seemingly unrelated regression，SUR)方法对上述方程组进行系统估计，为满足式(5)的相关约束，根据Greene[36]所提供的方法，对前n-1个价格除以第n个价格，并且只估计前n-1个份额方程组。表3报告了SUR的估计结果。

表3回归结果显示，方程组中各农业生产要素投入份额对其价格的回归系数βii均>0，满足最小成本函数对要素价格非递减的理论约束；超过50%的回归系数在统计意义上显著，R2取值均>0.8，说明各个方程对真实情况拟合效果较好。因此本研究的模型选择、变量设置以及估计方法等相对准确地反映中国玉米和圆白菜的生产状况，将基于表3的估计结果进行化肥需求价格弹性和要素替代弹性的计算。

4.2 化肥需求价格弹性

根据表3得到的成本份额系数βii的估计结果和相应的成本份额数据，运用式(10)计算出2004—2016年中国玉米和圆白菜生产的化肥需求价格弹性

表3 成本份额函数SUR估计结果Table 3 Cost share function SUR estimates

注：括号内的数值为异方差稳健标准误,***、**和*分别表示在1%、5%和10%水平显著。

Note：The values in brackets are Heteroskedasticity-Robust standard error. ***, ** and * mean significant effects of the variables at 1%, 5% and 10% levels, respectively.

(如图2所示)。由图2可知玉米和圆白菜的化肥需求价格弹性系数均<0，说明随着化肥价格的上升，其化肥投入量会出现下降，这意味着政府可以通过提高价格来降低农作物生产中的化肥投入。从数值大小看，玉米和圆白菜的化肥需求价格弹性分别为-0.12和-0.29，处于缺乏弹性的区间，说明化肥需求随价格变动的空间极为有限，通过调整化肥价格达到调节化肥投入的效果微乎其微。从变化趋势看，化肥的需求弹性在缺乏弹性区间内虽有波动，但并无脱离该区间的预期。

相较于玉米，圆白菜的平均化肥需求价格弹性高，说明圆白菜的化肥投入对价格变化的反应更加敏感，这一定程度上体现了经济作物与粮食作物之间的差别。经济作物生产与市场联结更加紧密，其产品价格更多由市场决定，因此，经济作物生产者对市场价格信息更敏感，对生产要素的价格变化反应也更敏感。粮食作物长期以来由于国家保障粮食安全政策需求，其生产目标在于持续增产以保障国家粮食供应，因此，在粮食收购保护价等政策作用下，其要素需求对市场价格变化敏感性相对较差。对比两者变动趋势可以发现，玉米的化肥需求价格弹性从2011年起呈现增长趋势，而圆白菜则总体呈现下降趋势，一个可能的原因是2011年国务院颁布的“十二五”期间全国现代农业发展规划(2011—2015)中关于粮食增长以及加强农业生态环境治理的相关政策对玉米生产产生了一定影响。

图2 玉米和圆白菜的化肥需求价格弹性
Fig.2 Demand price elasticity of fertilizer for corn and cabbage

4.3 要素替代弹性

根据表3得到的成本份额系数βii的估计结果，结合式(10)和(12)可以计算出2004—2016年中国玉米和圆白菜生产中化肥-劳动替代弹性(如图3所示)、化肥-机械替代弹性(如图4所示)。具体来看，SESij>0说明要素之间存在替代关系且数值越大替代关系越强；SESij<0说明要素之间存在互补关系且数值越大互补关系越强；SESij=0则说明要素之间不存在互补或替代关系。

图3 玉米、圆白菜生产的化肥-劳动替代弹性
Fig.3 Elasticity of substitution of fertilizer-labor of corn and cabbage production

从化肥-劳动替代弹性的总体数值看，2004—2016年玉米和圆白菜生产过程中化肥和劳动存在弱替代关系且数值呈明显下降趋势。图3表明，2011年后，玉米的化肥与劳动之间由替代关系转变为互补关系并逐渐加强，而在此期间玉米产量增长趋势总体上升，说明玉米产量变化导致的化肥投入量变化对化肥-劳动替代弹性没有显著影响。未来由于人口红利逐渐消失，中国劳动力价格将持续上涨，将一定程度上减少当前玉米生产中的化肥投入，但对当前圆白菜生产中的化肥投入基本没有影响。

从化肥-机械替代弹性的总体数值看，2004—2016年玉米生产的化肥与机械投入存在较强的替代关系，而圆白菜生产则存在较强的互补关系。图4表明，随着时间的推移，玉米生产过程中化肥与机械投入的替代关系强度缓慢下降，但其替代弹性数值始终>0.5，说明玉米生产过程中化肥投入过量而机械投入量不足，每增加一单位机械投入所带来的边际收益远远高于增加一单位化肥投入所带来的边际收益。故当农机补贴等政策导致机械价格下降时，农户会选择增加机械投入同时减少化肥投入，反之，农户会减少机械投入，重新依靠增施化肥来保证粮食产量。相应地，导致圆白菜生产过程中化肥与机械之间呈现互补关系的原因可能是：圆白菜生产作为城郊农业，其种植规模相对于水稻、小麦、玉米等大田作物较小，无法进行大规模机械化生产，因此机械对于圆白菜生产的促进作用主要体现在利用施肥机等辅助施肥手段进行集约化作业，作为对劳动的要素替代(3)事实上，结合图3所提供的圆白菜生产过程中化肥与劳动的替代关系，并利用SES弹性公式进行计算，可以得到圆白菜生产过程中机械和劳动之间同样存在替代关系，因而其化肥与机械投入呈现互补关系。。由此可见，政府可以通过价格政策适当减少玉米生产所使用的机械价格，并增加圆白菜生产所使用的机械价格，以减少二者的化肥投入。

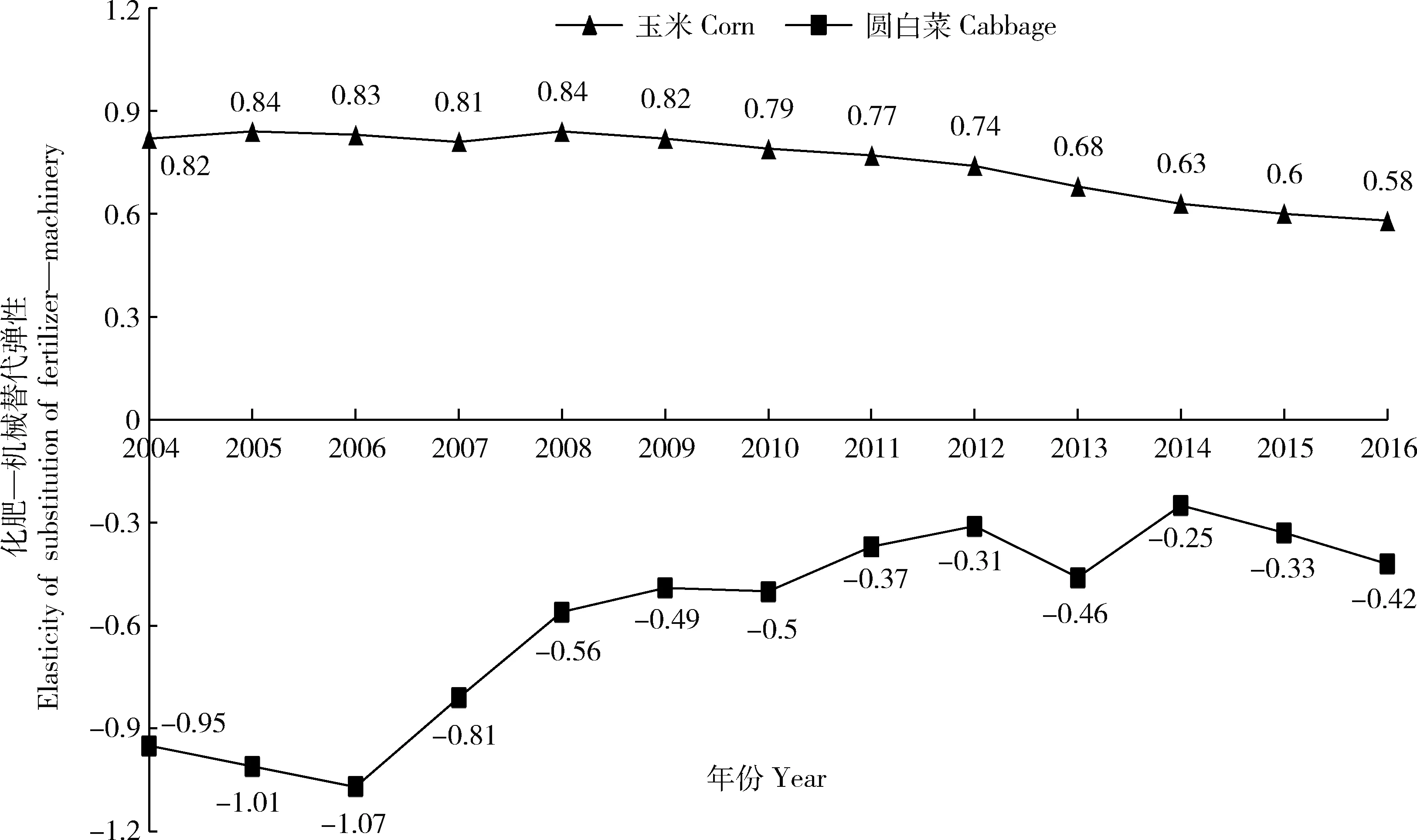
图4 玉米、圆白菜生产的化肥-机械替代弹性
Fig.4 Elasticity of substitution of fertilizer-machinery of corn and cabbage production

5 结论与政策启示

5.1 研究结论

本研究在对国内外关于农业生产要素需求和替代弹性、农业化肥投入影响因素等已有研究成果进行梳理的基础上，通过构造超越对数成本函数和影子替代弹性，利用2004—2016年中国主要玉米和圆白菜产区的化肥及其他要素投入与价格数据，采用似不相关回归方法实证分析了中国玉米和圆白菜生产中化肥的需求价格弹性，化肥和劳动的替代弹性以及化肥和机械的替代弹性。本研究得到的结论主要包括：第一，化肥价格、劳动价格和机械价格等各类价格变量对玉米生产中的化肥投入量具有显著影响；化肥价格对圆白菜生产中的化肥投入量具有显著影响，其他变量不显著。第二，玉米、圆白菜的化肥需求价格弹性分别为-0.12和-0.29，均处于低弹性区间且接近区间下限，表明化肥价格变化对玉米和圆白菜生产中化肥投入的影响较小，通过调整化肥价格很难影响其化肥投入；圆白菜的化肥需求价格弹性整体高于玉米，说明圆白菜生产中的化肥投入对价格变化反应相对更加敏感。第三，玉米的化肥和劳动投入存在互补关系，劳动价格的上升会导致化肥投入的少量下降；圆白菜的化肥和劳动投入存在微弱替代关系(替代弹性<0.10)。第四，玉米的化肥和机械投入存在替代关系且富有弹性，圆白菜的化肥和劳动存在互补关系，但随着时间推移，玉米和圆白菜生产中化肥和机械的替代/互补关系均逐渐减弱。

5.2 政策启示

基于上述研究结论，本研究可以为化肥减施政策提供3点启示：第一，谨慎采用通过提高化肥价格降低化肥投入的政策。化肥的低需求价格弹性使得政府即使大幅提高化肥价格也不能有效减少农作物生产中的化肥投入，过高的化肥价格反而会增加农户种植成本，损害农户利益；政府可以运用稳健的价格政策，一定程度上提高价格，同时主要利用非价格政策调控化肥投入。第二，适当通过价格政策调整农业机械价格对农业生产中的化肥投入进行调控。结合要素投入替代弹性的差异并考虑生产实际，对玉米生产所需的机械设备进行价格补贴等可以有效降低玉米生产过程中的化肥投入；减少圆白菜生产所需机械设备的价格补贴，提高圆白菜生产的机械价格，也可有效降低圆白菜生产过程中的化肥投入。第三，加强对农业劳动力的教育投入与技能培训，培育新型农业人才。通过教育与培训，提升农民的非农就业技能或者农业经营能力，间接推动农业劳动力价格提升，降低玉米生产中的化肥投入；人力资本较高的农民，其掌握并采用科学施肥技术的可能性更高，不仅可以降低玉米生产中的化肥投入，对圆白菜生产中缺乏替代弹性的化肥投入也有减少作用。