RPC叠合简支梁受弯承载力分析

曹 霞,杨振轩,张金丹,金奇志

(1.桂林理工大学 广西建筑新能源与节能重点实验室,广西 桂林 541004;2.贺州学院 建筑工程学院,广西 贺州 542899)

0 引 言

活性粉末混凝土(reactive powder concrete,RPC)[1]是一种超高强度、高耐久性、高韧性、体积稳定性好的新型材料,叠合结构是建筑业推广的重要结构,因此将RPC应用于叠合结构具有重大意义[2]。何大治[3]分析了叠合构件设计参数αM和αh对叠合构件极限承载力的影响;过民龙等[4]对T形RPC-NC叠合梁进行了静载试验,研究了RPC受拉区高度、NC强度等级以及配筋率对组合梁受弯性能的影响;曾垂军[5]对U形和T形预应力混凝土叠合梁进行受弯试验，配筋适当的预应力混凝土叠合梁与整浇对比梁的整体破坏特征基本相同;袁海梅[6]对新型叠合梁进行受弯性能研究，通过与普通混凝土叠合梁比较表明，新型叠合梁具有良好的承载力，柱节点整体性更好，刚度更大，梁端塑性变形能力更强；张多新等[7]分析了二次受力混凝土叠合梁在受力过程中受拉钢筋“应力超前”、后浇混凝土“受压应变滞后”和截面内力转移等机理;王磊等[8]对6根受拉区新增受力钢筋的混凝土叠合梁进行了受弯性能试验，研究表明，叠合层水平粘结裂缝的出现一定程度上对受弯裂缝的开展起到了阻碍和延缓作用，加速了应力重分配的进程，并且叠合梁的极限承载力以及屈服强度都比同等条件下整浇梁低;朱智俊[9]研究了预制梁高度、后浇层厚度、有效预应力大小以及后浇层混凝土等因素对活性粉末混凝土预应力叠合梁受弯承载力的影响;马远荣[10]采用不同的计算模型和应力等效模式计算叠合梁的受弯承载力。

目前,对普通混凝土叠合构件的研究比较成熟,但对RPC叠合构件研究相对较少。 因此,本文通过试验,对RPC叠合面应变进行分析,研究不同预制高度对RPC叠合梁正截面受力性能的影响。

1 试验概况

试验共设计了1根整浇梁和2根叠合梁,试件基本参数见表1,试验加载图如图1所示。

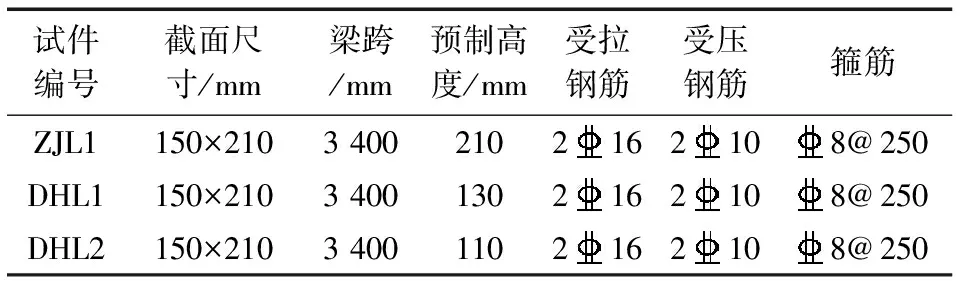
表1 试件基本参数Table 1 Parameters of specimens

图1 试验加载图Fig.1 Diagram of test loading

RPC的主要原料: 普通硅酸盐42.5级水泥;密度为2.223 g/cm3,颗粒大小<2 μm,平均粒径±0.31 μm的硅灰; 0.60～1.25 mm粗粒径砂、0.30～0.60 mm中粒径砂和0.160～0.315 mm细粒径砂组成的石英砂; 长度为12～15 mm,直径为0.22 mm,长径比为55～68,抗拉强度为2 300 MPa的钢纤维; E12改性聚羧酸减水剂以及普通自来水。 RPC配合比、RPC材料及钢筋力学指标见表2～4,混凝土应变测点布置见图2。

2 试验结果分析

2.1 开裂弯矩与极限弯矩

当试件达到开裂弯矩时,叠合面结合良好,未出现开裂的现象,叠合梁的开裂位置在预制部分的下部。由试验测得的试件开裂弯矩Mcr与极限弯矩Mu见表5,各试件破坏形态均为适筋破坏。

表2 RPC配合比Table 2 Mix of RPC

注:钢纤维以体积率计。

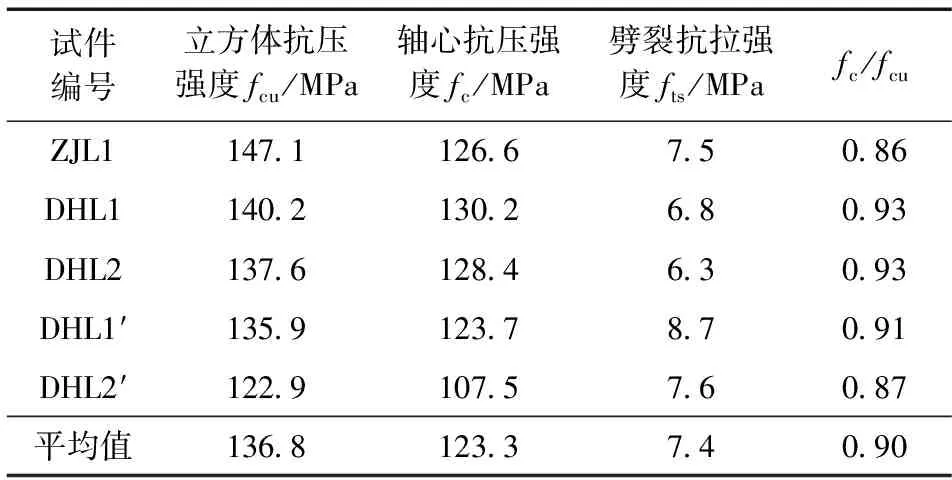
表3 RPC力学指标实测值Table 3 Measured mechanical indices of RPC

注：DHL1′ 、DHL2′为二次浇筑混凝土随梁一起浇筑的试块。

表4 钢筋力学指标实测值

Table 4 Measured mechanical indices of reinforcement MPa

随着预制高度的减小,试件的开裂弯矩分别下降16.2%和31.7%,极限弯矩分别下降11.2%和14.2%;ΔM为开裂荷载与极限荷载的差值,体现构件带裂缝抗弯工作能力[11],随着预制高度的减小,试件带裂缝抗弯工作能力有所削减。

2.2 叠合面受力分析

为保证叠合梁预制部分和后浇部分形成整体,共同工作,将叠合面抹平后再进行交叉划毛,深度约6 mm,使叠合面凹凸不平,提高叠合面的水平抗剪能力,二次浇筑前将叠合面表面清理干净,刷素水泥浆一道以保证上下叠合面粘结良好。叠合面处理如图3所示。

表5 试件开裂弯矩与极限弯矩

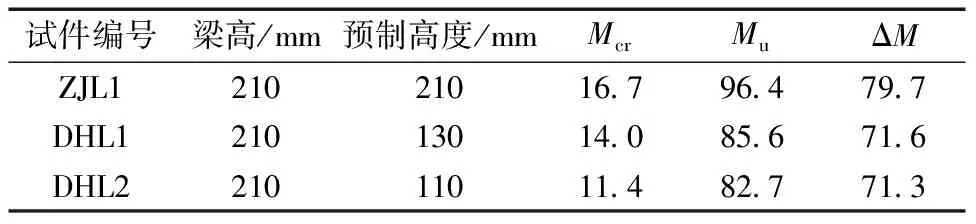
Table 5 Cracking moment and ultimate moment of specimensM/(kN·m)

图3 叠合面处理Fig.3 Treatment of composite surface

2.2.1 叠合面纯弯段混凝土应变分析 在达到开裂荷载前,叠合面上下混凝土应变基本重合; 随着荷载的增加,叠合面上端混凝土应变略小于叠合面下端混凝土,符合后浇混凝土受压的“应变滞后”现象。当DHL1纯弯段混凝土应变达到约500 με时,跨右叠合面上端混凝土应变突然增加(图4),这是因为叠合面产生了水平裂缝。DHL1在破坏时叠合面处出现了长150 mm、宽0.02 mm的水平裂缝,裂缝开展详见图5。

2.2.2 叠合面弯剪段混凝土应变分析 由图6可知,同一试件同一位置上下叠合面处混凝土应变趋势基本一致,同一试件不同剪跨区应变也大致相同,说明试件剪跨区叠合面上下粘结性能良好,左右剪跨区受力较均匀。DHL2右剪跨区测点右31与右32差别较大,是由于裂缝发展至叠合面下端,导致下端测点右32应变发展较快,裂缝未经过叠合面向上延伸,因此叠合面上端测点右31应变值较小,裂缝开展详见图7。

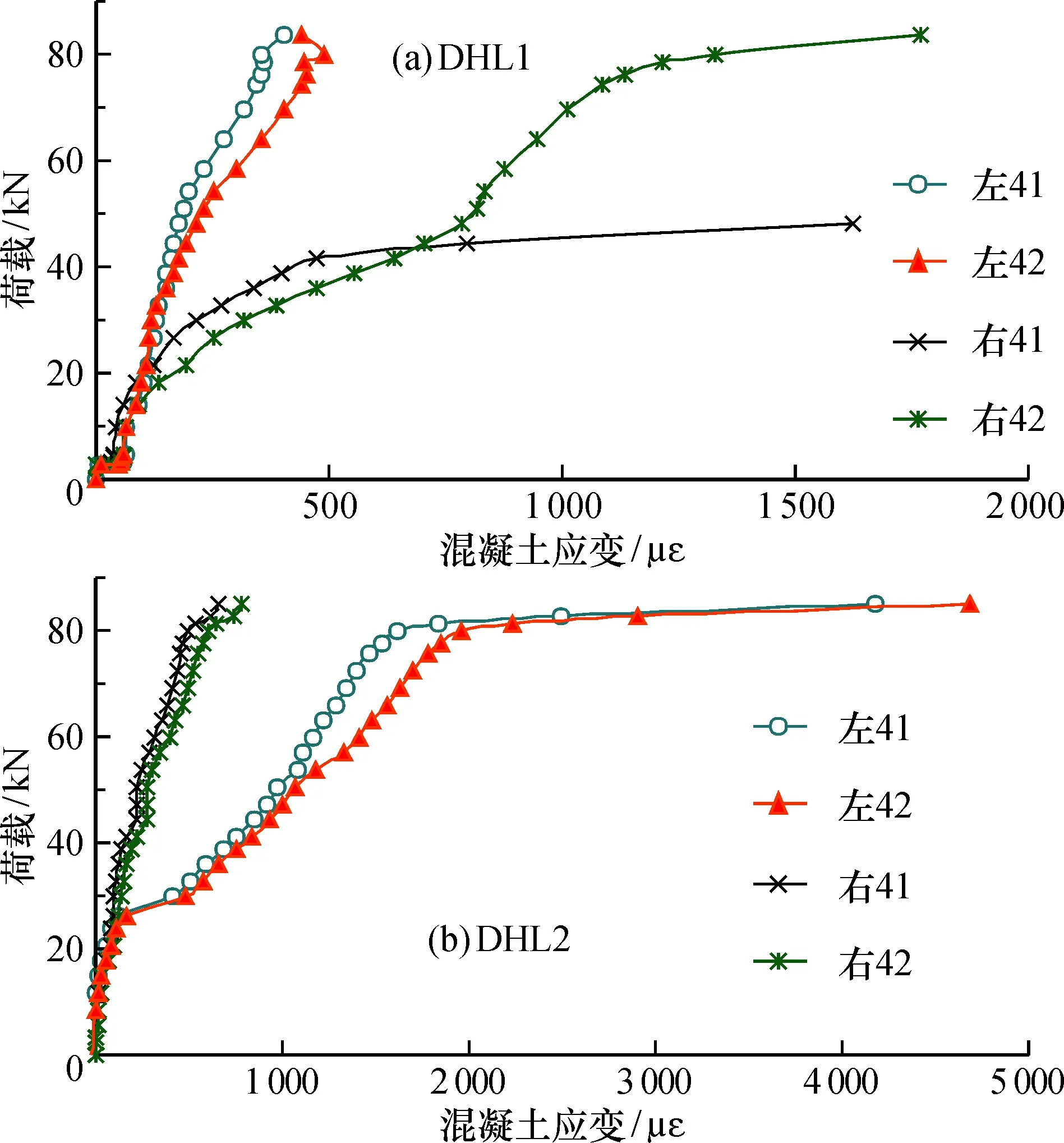
图4 各试件纯弯段叠合面混凝土应变Fig.4 Concrete strain on composite surface of pure bending section in each specimens

图5 DHL1裂缝分布图Fig.5 Cracks distribution of DHL1

图6 各试件剪跨段叠合面混凝土应变曲线Fig.6 Concrete strain on composite surface of shear span section in each specimens

图7 DHL2裂缝分布图Fig.7 Cracks distribution of DHL2

2.3 平截面假定的验证

根据各试件混凝土的应变量测值,绘制跨中截面处随梁高度变化混凝土的平均应变,如图8所示。

梁未出现裂缝之前,梁底部的RPC和纵向钢筋共同受力,梁截面应变为线性分布,大致为三角形。 沿梁同一截面不同高度上RPC的平均应变在未开裂前表现出良好的线性关系,并且中和轴位置基本位于梁高的一半位置处,说明RPC抗拉强度高,裂缝较少且发展不充分,未引起中和轴上移,在各级荷载作用下混凝土的平均应变基本符合平截面假定。 叠合梁的预制高度均超过梁高的一半,即中和轴位置均在预制部分,所以本试验构件RPC预制高度对中和轴位置几乎没有影响。

3 RPC叠合梁正截面受弯承载力计算分析

3.1 正截面应力图形的等效

根据混凝土应力的合力大小相等且作用点不变的原则,将RPC叠合梁正截面应力曲线图形用等效的矩形应力图形替代,如图9所示。

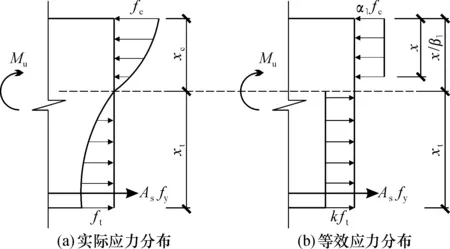
图9 等效矩形应力分布图Fig.9 Equivalent rectangular stress block

RPC叠合梁受压区等效矩形应力图形由等效矩形应力图系数α1和β1确定。

(1)

(2)

式中:εcu为混凝土极限压应变,εcu=0.005 5[12];Tcu为混凝土压应力-应变所围面积;ycu为相应面积形心到压应力轴的距离。 联立式(1)和式(2),可得α1=0.88,β1=0.76[13]。

RPC叠合梁受拉区等效应力图系数k推导过程:

由截面水平力平衡可得

α1fcbx=Asfy+kftbxt,

(3)

对钢筋合力点取矩可得

(4)

式中:As为纵向受拉钢筋截面面积;fy为纵向受拉钢筋屈服强度;Mu为RPC叠合梁受弯承载力;ft为活性粉末混凝土抗拉强度;as为受拉钢筋合力点到受拉区边缘的距离;xt为混凝土受拉区高度,即xt=h-xc=h-x/β1(其中，h为梁正截面高度；x为等效矩形应力图的混凝土受压区高度；xc为混凝土受压区高度)。

图8 各试件跨中正截面混凝土应变Fig.8 Concrete strain on composite surface of cross normal section in each specimens

联立式(3)和式(4),由实测的极限弯矩Mu,可得受拉区等效系数k值(表6)。

表6 各试件受拉区等效系数k值Table 6 Tensile stress equivalent coefficients of specimens

从试验现象可以看出,3根试验梁均为适筋梁破环,即受拉区RPC对构件截面承载力有一定的贡献。从试验梁受拉区等效系数k值可以看出,受拉区RPC对构件截面受弯承载力的贡献随着预制高度的变化而变化,预制高度越小,RPC叠合梁达到受弯极限承载能力时,受拉区塑性变形越小,塑性化发展程度越小,从而受拉区混凝土对截面受弯承载力贡献越小。由于钢纤维在构件开裂时将“桥接”于裂缝,在一定程度上提高了RPC的抗拉强度,但由于钢纤维过细易被腐蚀,在计算承载能力时不应考虑钢纤维的有利影响。综上所述,偏于安全取受拉区等效系数k=0.55。

3.2 正截面受弯承载力计算公式

根据平衡条件和上述推导结果可得RPC叠合梁正截面受弯承载力计算式:

(5)

将本文的试验数据与文献[3]的相关数据代入式(5)得到极限承载力计算值,并将试验值与计算值进行对比,结果见表7。

3.3 界限受压区高度和最大配筋率

根据平截面假定和界限相对受压区高度的定义ξb可得

(6)

表7 试验梁承载力试验值与计算值比较

Table 7 Comparison between experimental value and calculated value for bearing capacity test beamM/(kN·m)

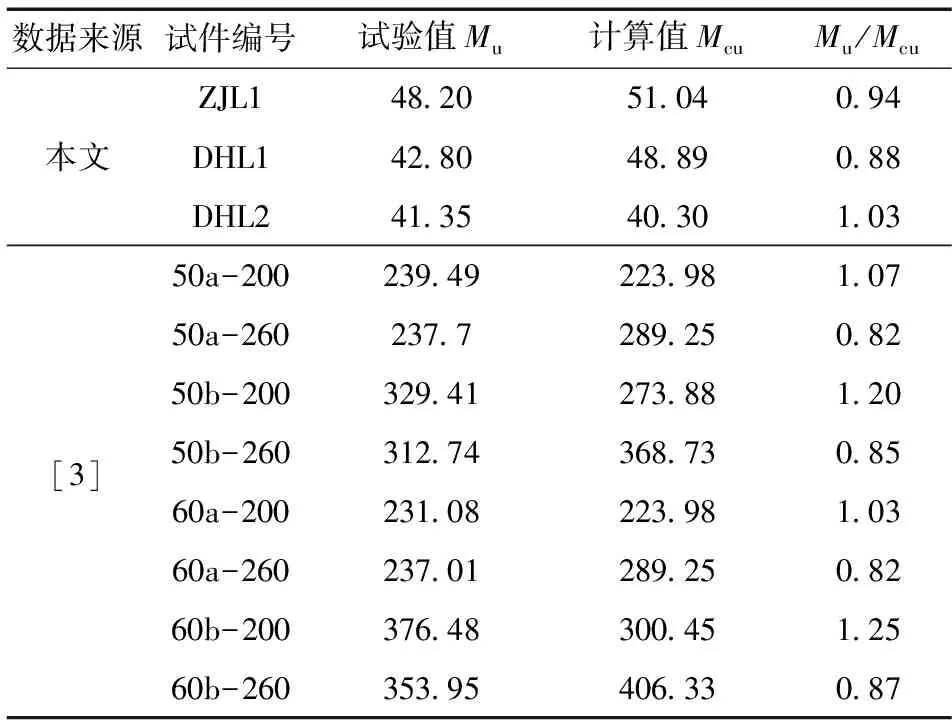
数据来源试件编号试验值Mu计算值McuMu/McuZJL148.2051.040.94 本文DHL142.8048.890.88 DHL241.3540.301.03 50a-200239.49223.981.07 50a-260237.7289.250.82 50b-200329.41273.881.20 [3]50b-260312.74368.730.85 60a-200231.08223.981.03 60a-260237.01289.250.82 60b-200376.48300.451.25 60b-260353.95406.330.87

式中:β1、εcu与上述取值相同;εy、fy分别为钢筋的屈服应变、屈服强度;Es为钢筋的弹性模量,取2.0×105MPa。

将材料特征值代入式(6),可求得RPC叠合梁界限相对受压区高度ξb=0.58,而配置相同钢筋的C80普通混凝土界限相对受压区高度ξb=0.46,这是由于RPC极限压应变比普通混凝土要大,具有更好的塑性。

由式(3)和式(6)可得最大配筋率ρmax为

(7)

将试验数据代入式(7),得到本试验构件RPC叠合梁的最大配筋率为14.7%。

4 结 论

(1)随着预制高度的减小,RPC叠合梁的开裂弯矩降幅为16.2%和31.7%,极限弯矩降幅为11.2%和14.2%,且RPC叠合梁的带裂缝受弯工作能力也有所削减。

(2)在达到开裂荷载前,叠合面上下混凝土应变基本重合;随着荷载的增加,叠合层混凝土应变略小于预制层混凝土应变,符合后浇混凝土受压的“应变滞后”现象。

(3)考虑不同预制高度对受弯承载力的影响,推导了RPC叠合梁受弯承载力计算建议式,计算结果与实测结果吻合较好。本试验构件RPC叠合梁的界限受压区高度ξb=0.58,最大配筋率为14.7%。