基于压汞实验的致密油储层孔隙分形特征分析
——以鄂尔多斯盆地定边油田延长组长7油层为例
白耀文,张 刚,李春生,任 剑,丁文龙,尹 帅,肖子亢
(1.延长油田股份有限公司定边采油厂,陕西 定边 718699; 2.延长油田股份有限公司,延安 716000; 3.中国地质大学(北京) 能源学院,北京 100083; 4.西安石油大学 地球科学与工程学院,西安 710065)
世界石油工业已经步入非常规油气工业发展阶段,致密油则是非常规石油中最为“常规”的一种,也是当前油气勘探开发最为现实的领域[1-3]。 致密油储层泛指孔隙度低于12%,覆压渗透率低于0.1×10-3μm2的页岩、砂岩及灰岩等各类岩性的致密储层[2]。 本文所指的致密油特指致密砂岩储层。 美国是世界上致密油开发最为成功的国家,在约20个盆地内均发现了致密油分布,其中2014年致密油产能已超过2×108t,占原油总产能的1/3,实现了致密油的稳步建产及对常规油气的顺利接替[1]。我国也蕴藏了丰富的致密油资源,得益于钻完井及压裂技术的进步,目前在鄂尔多斯盆地、渤海湾盆地及松辽盆地等地区均实现了致密油的商业开发[4-6]。致密油储层具有复杂的孔隙结构及强各向异性,储层评价难度大,目前国内尚未建立有效的致密油储层参数评价体系及标准。致密油储层参数的准确评价是其资源量评价及制定有效开发方式的基础[7]。因此,有必要采用不同的技术手段对致密油储层微观孔隙结构进行评价。
虽然一些实验方法(如薄片观察、压汞、液氮吸附等)能对致密储层内部的孔隙分布进行评价,但不能直接建立岩石内部孔隙分布复杂程度的定量函数关系。 此时,通过引入分形理论,可实现致密储层内部孔隙结构分布特征的定量关系模型。 Mandelbrot[8]最早将分形理论方法引入到油气储层评价中; Pfeifer等[9]基于吸附实验证明了岩石内部孔隙具有分形特征; Yang等[10]利用分形理论探讨了致密储层内部孔隙的自相似结构; Li等[11]探讨了强非均质性页岩气储层分形维数的影响因素; 公言杰等[12]利用高压压汞技术建立了致密油流动孔隙度下限的识别标准。 分形理论原理简单,在业界被广泛推广应用,适用于强非均质性致密油储层孔隙结构评价。 本文以鄂尔多斯盆地定边油田延长组致密油储层为例,利用高压压汞实验和分形原理分析了目的层砂岩的分形特征。 同时,探讨了岩石分形特征参数对岩石渗透率的影响。
1 孔隙分形原理
根据分形原理,将一个具有一定结构的实体划分为N个单元,则其单元数N与单元长度r之间具有幂指数关系
N=C/rD,
(1)
式中:C为比例常数,D为分形维数。
根据Kozeny-Carman方程,孔隙空间由毛细管束组成。 以具有固定半径为V(r)的孔隙空间作为一个单元,可以得到[13-15]
N=V(r)/(πr2l),
(2)
式中:r为孔隙半径;l为毛细管的长度。 不同的单元之间具有自相似性,表现为具有相同的孔隙半径和毛细管比值。 作一个简单的假设,即r=l,联合式(1)和式(2),则具有固定半径的孔隙体积可以表示为
V(r)=Nπr3=Cπr3-D,
(3)
对孔隙体积分布进行微分处理可得
(4)
半径小于r的孔隙的累计体积可以表示为
(5)
通过求解可进一步得到
(6)
由于孔隙空间的分布遵循分形规律,岩石的总孔隙体积为

(7)
式中:rmax和rmin分别为最大和最小孔隙半径。 孔隙半径小于r的孔隙累积体积分数为
(8)
由于rmin≪r,因此可以得到

(9)
对于一个半径为r的圆柱形孔隙,入汞压力值(Pc)的大小与注入流体及替代流体之间的表面张力(σ)及接触角(λ)有关
(10)
考虑到Pc与r之间为反比关系,同时,Pc min=2σcosλ/rmax,即最小的入汞压力是与最大孔隙半径(rmax)相关的。 因此,式(8)中的累积孔隙体积分数(Vc)与入汞压力比(Pc/Pcmin)之间具有如下关系[14]
(11)
对于非润湿相流体替换润湿相流体的情况,Vc代表残余的润湿相流体的饱和度。 因此,该式代表了随着入汞压力(Pc)的增加,岩石内部残余润湿相流体的饱和度逐渐减小的过程。 与此同时,非润湿相流体逐渐进入岩石的孔隙中,相应其饱和度逐渐增加。 对式(11)两侧分别取对数得到
logVc=(D-3)logPc-(D-3)logPcmin。
(12)
可见,logVc与logPc之间具有线性关系,根据这两个参数的双对数曲线的斜率可以求取岩石孔隙的分形维数(D)。 分形维数又称为压汞分形维数(Dcp),D=Dcp。
2 压汞实验
2.1 研究区及样品信息
研究区位于鄂尔多斯盆地定边油田,大地构造上位于鄂尔多斯盆地陕北斜坡中部的西段。 该地区构造平缓,主要发育少量低幅鼻状构造,无断裂。 延长组长7油层组是该地区的主要致密油勘探开发目的层,本文砂岩样品即取自延长组长7油层1段。 区内长7油层1段的埋深介于2 000~2 600 m,致密油储层的主要岩性为粉砂岩、粉细砂岩、细砂岩及泥质粉砂岩。 其沉积微相主要包括河口坝、水下分流河道、分流间湾、席状砂及湖泥等。 样品取自7口井,共计11组,编号分别为D1~D11,样品具体信息见表1。
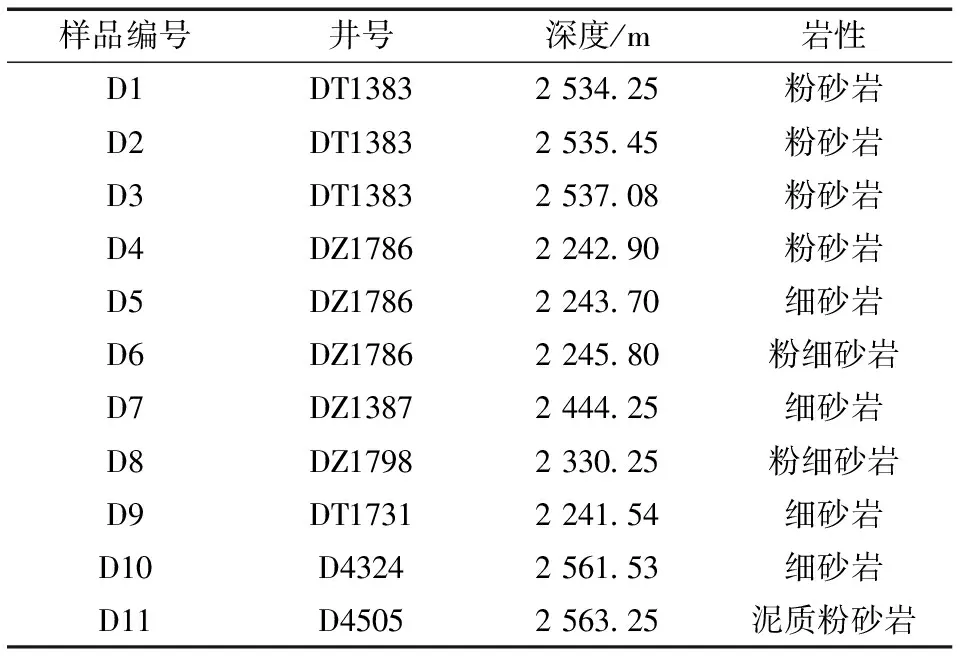
表1 实验测试样品基本信息Table 1 Basic information of experimental samples
2.2 高压压汞实验
实验设备为Micromeritics公司生产的Autopore Ⅳ压汞仪,最高压力为30 000 psi(204 MPa),测量的孔径范围在0.006 ~360 μm。 实验测试标准和数据处理方法参照《岩石毛管压力曲线的测定》(SY/T 5346—2005)。仪器的测试条件为:汞表面张力480 mN/m,汞接触角140°,1个高压站和2个低压站。压汞曲线可反映连通性孔喉结构特征,实验过程中,进汞过程为非润湿相驱替润湿相。当注入压力增加到突破更细小的孔喉毛管压力时,进汞饱和度逐渐增加。
3 实验结果及分析
3.1 压汞特征参数
11组砂岩样品的压汞曲线如图1所示,部分砂岩样品的显微薄片特征如图2所示。各砂岩样品的最大入汞饱和度分布在6.99%~81.08%,平均值为64.72%。对于具有较大入汞饱和度的样品,其物性较好;而对于入汞饱和度较低的样品,其物性较差,如D11号样品,其孔隙度最低(3.11%,图2d),入汞量仅有6.99%。

图1 测试样品压汞曲线Fig.1 Mercury intrusion curves of the samples

图2 部分砂岩样品显微薄片特征Fig.2 Microscopic characteristics of partial sandstone samplesa—碎屑成分主要为石英,其次为长石(主要为微斜长石),颗粒分选中等,以次棱角状-次圆状为主,线-缝合接触;b—碎屑成分主要为石英,其次为长石(主要为斜长石),颗粒分选中等,磨圆好,主要为点接触; c—碎屑成分主要为石英,其次为长石,碎屑颗粒分选中等,磨圆较好,颗粒多为点-线接触,孔隙较为发育; d—碎屑成分主要为石英,其次为长石,孔隙多被黏土充填,颗粒分选较差,以次棱角状为主,多为点-线接触
各组样品的退汞效率分布在15.55%~68.35%,平均值为28.3%。对于致密砂岩储层来说,通常认为当其退汞效率>50%时,岩石内部孔隙系统具有较好的连通性[15]。相比而言,研究区长7致密油储层内部孔隙系统的连通性较差。
较差的孔隙连通性与孔隙尺寸、孔喉配比、微裂缝发育程度及沉积体系非均质性等方面因素有关[16]。这些因素导致在退汞过程中,岩石内部将有大量汞滞留在孔隙中。在致密油开发过程中,将会有大量剩余油无法被开采。各组测试样品的进汞和退汞曲线之间存在滞后环(图1),且两曲线之间的体积差较大,表明岩石中以张开孔为主。但对于D11号样品,入汞及退汞曲线之间的体积差较小,表明其内部主要为封闭及半封闭孔。
利用压汞法确定的测试样品的压汞特征参数如表2所示。D1~D3、D7~D9及D11号样品为致密砂岩,而D4~D6及D10号砂岩样品的物性相对较高,为中砂岩。
各致密砂岩样品的均值系数(ζ)较大,而中砂岩的均值系数要相对小一些。从图3可看出,长7油层中的致密砂岩和中砂岩的孔喉配置具有较大的差异。较大的均值系数表明岩石内部的微孔居多;而当均值系数较小时,表明岩石内部还有一定数量的中孔及大孔。
所有砂岩样品的分选系数和歪度均偏大,且变异系数较小,这些特征表明所测试砂岩样品的孔喉配比关系较差,以微小孔居多。 从图1所示的压汞曲线也可看出,各测试样品的退汞曲线均具有突降的特征,表明岩样内部的细颈型孔隙的含量较高。根据测试样品的压汞特征参数结果可以看出,目的层砂岩内部主要发育微孔,且孔隙间的连通性较差,对致密油的开发不利。

图3 测试岩样的孔喉半径分布特征Fig.3 Distribution characteristics of pore throat radius of the samples

表2 测试砂岩样品的压汞特征参数Table 2 Test results of mercury intrusion test parameters of the sandstone samples
注:φ—孔隙度;k—渗透率;ζ—均值系数;ψ—分选系数;δ—歪度;η—变异系数;Rmax—最大孔隙半径;Rav—平均孔喉半径;SHgm—最大入汞饱和度;SHgx—退汞效率;χ—平均孔喉比。
3.2 孔隙分形特征
利用高压压汞试验结果及分形原理对岩石孔隙的分形特征进行分析。累积孔隙体积分数(Vc)与入汞压力(Pc)之间的双对数关系,可确定所测试砂岩样品的分形维数(Df),分布样品的数据拟合结果如图4所示。 可见,所测试数据的线性关系十分显著。 根据曲线的斜率可以求得各组样品的Df值(表3)。从拟合曲线的相关系数来看,其值较高,表明所计算的分形维数值可靠。
同时,本文还对岩石的毛细管平均迂曲度分形维数(DT)进行了计算。 岩石内部的孔隙空间通常假设为由毛细管束组成,因此,DT可用于表征岩石内部毛管束的复杂程度,其取值范围为1~3。DT的计算公式为[17]

图4 测试岩样log Vc与log Pc之间的关系Fig.4 Relationship between log Vc and log Pc of the samples
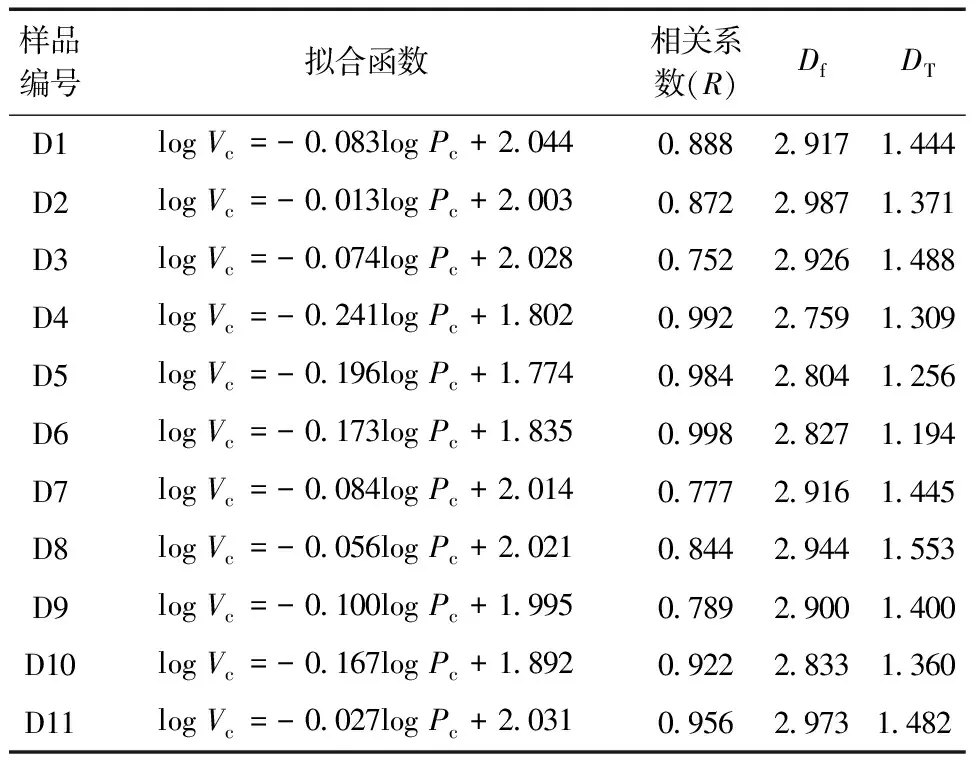
表3 各组测试样品分形维数计算结果Table 3 Calculation results of fractal dimensions of the samples
(13)
式中:Tav—毛细管平均迂曲度;Rav—平均毛细管半径,μm;Lm—二维空间毛细管特征长度。Tav和Lm的表达式分别见式(14)、(15)[18-19]。
(14)
(15)
式中:φ—孔隙度,%;Rmax—最大孔喉半径,μm。
测试样品的毛细管平均迂曲度分形维数(DT)计算结果见表3。 砂岩样品的Df分布在2.759~2.987,平均值为2.890;DT分布在1.194~1.553,平均值为1.391,且Df>DT。 岩石的分形维数值(Df)主要反映岩石的非均质性、孔喉分布及孔隙表面粗糙程度等孔隙结构特征,该值越大,表明岩石孔隙结构越为复杂、孔隙间连通性越差,且岩石内部的非均质性越强。 致密砂岩的Df值明显大于中砂岩,致密砂岩的Df平均值为2.938,而中砂岩的Df平均值为2.806。 致密砂岩的DT值也略大于中砂岩, 致密砂岩的DT平均值为1.455, 而中砂岩的DT平均值为1.280。该特征表明,致密油储层越致密,其内部的孔隙结构就越复杂。
3.3 分形特征参数对渗透率的影响
测试砂岩样品的孔隙度与渗透率间的关系见图5,两者间具有较好的正相关关系,表明孔隙度是控制致密砂岩储层渗透率的重要因素。分析测试岩样的Df及DT与岩石渗透率之间的关系,结果见图6。Df与DT均与致密砂岩的渗透率存在较好的负相关性,表明该致密砂岩储层的渗透率受孔隙结构的影响。
DT主要反映岩石内部毛细管状孔隙的平均迂曲度的微观结构。 毛细管状孔隙的概念最早由Carman[20]提出,目前已经被广泛认同。 该概念通过提出毛细管迂曲度(τ)参数,将抽象的毛管具体化。
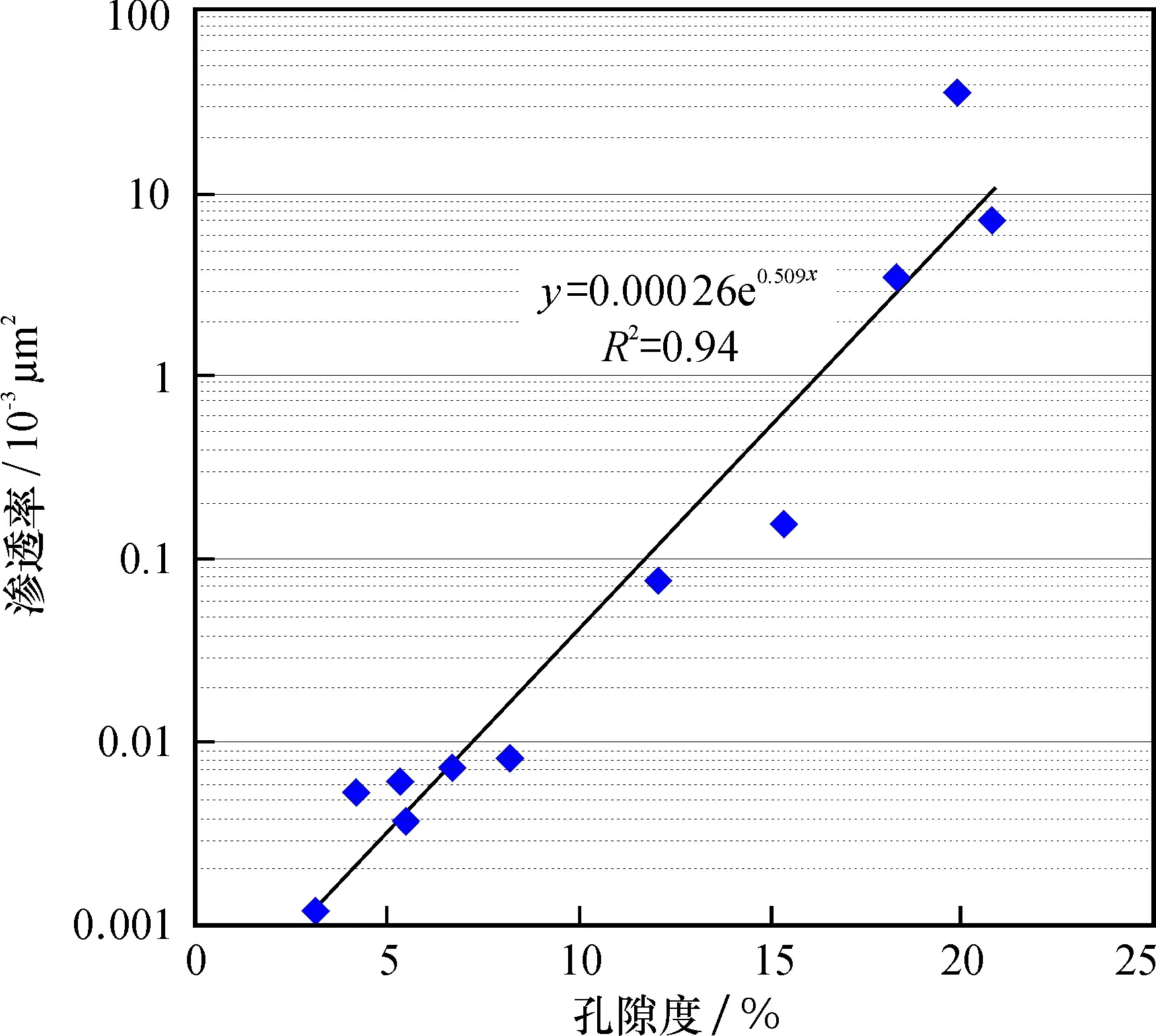
图5 测试岩样的孔隙度与渗透率之间的关系Fig.5 Relationship between porosity and permeability of the samples
τ定义为流体流过岩石孔隙的有效流动路径(Le)与岩心总长度(Lm)的比值为有效值(图7a)。 该假设对于常规中-高孔(φ>10%)砂岩储层来说是适用的[21]。 对于本文所研究的致密砂岩储层来说,镜下观察表明致密砂岩中的储集空间以近圆形孔隙团为主,微裂隙的发育程度较低,因此该假设也同样适用。
从两类岩性岩样的DT、Df与k之间的相互关系可以看出,两者间具有明显的负相关性(图6)。中砂岩的的Df值和DT值均较小,表明中砂岩内部微孔的分布规律较为规则,且毛细管迂曲度要相对小一些。而致密砂岩的Df值和DT值均较大,表明致密砂岩内部微孔的分布较为杂乱,孔隙间的连通性差;同时,其毛细管迂曲度较大,因此流体渗流所需通过的路径较长,这是造成其渗透率低的重要原因。据此,可建立两类砂岩的等效孔隙排列及毛管迂曲度模型,见图7b。
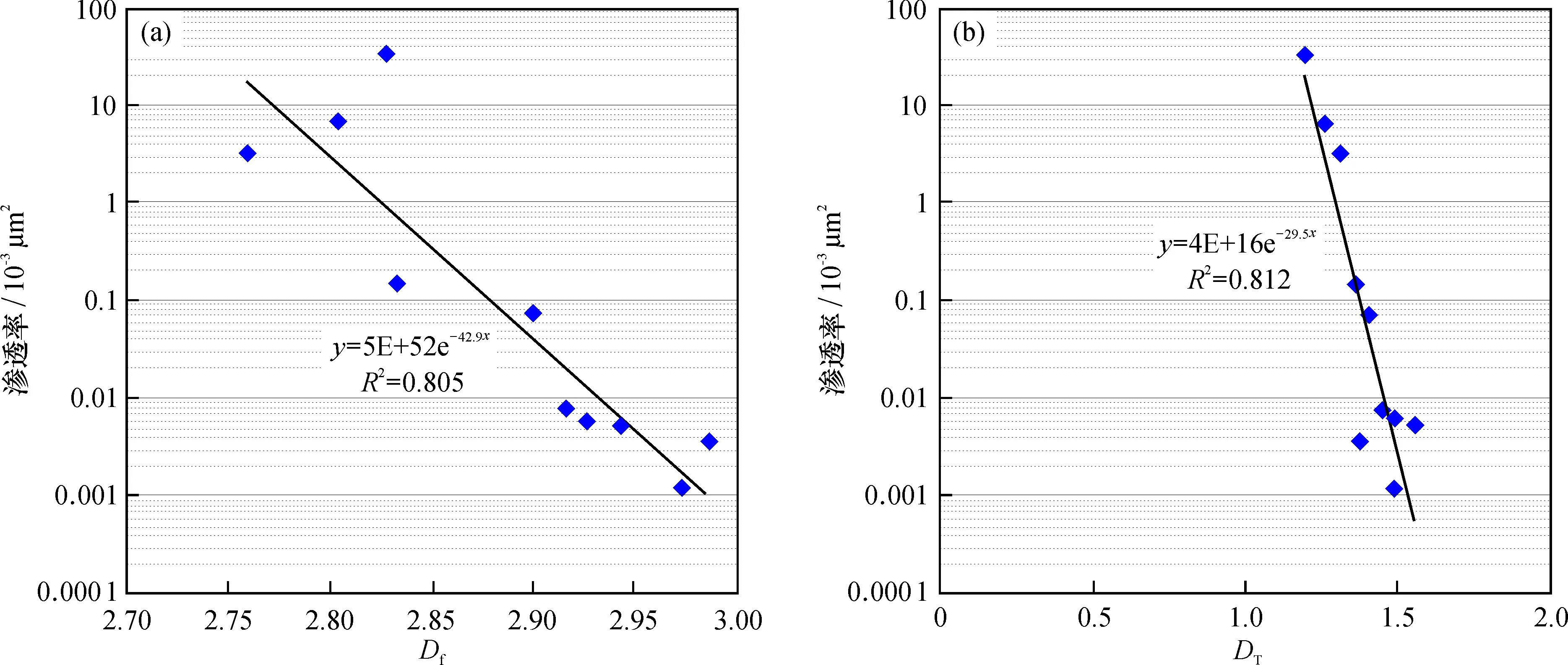
图6 分形特征参数对岩石渗透率的影响Fig.6 Influence of fractal parameters on rock permeability
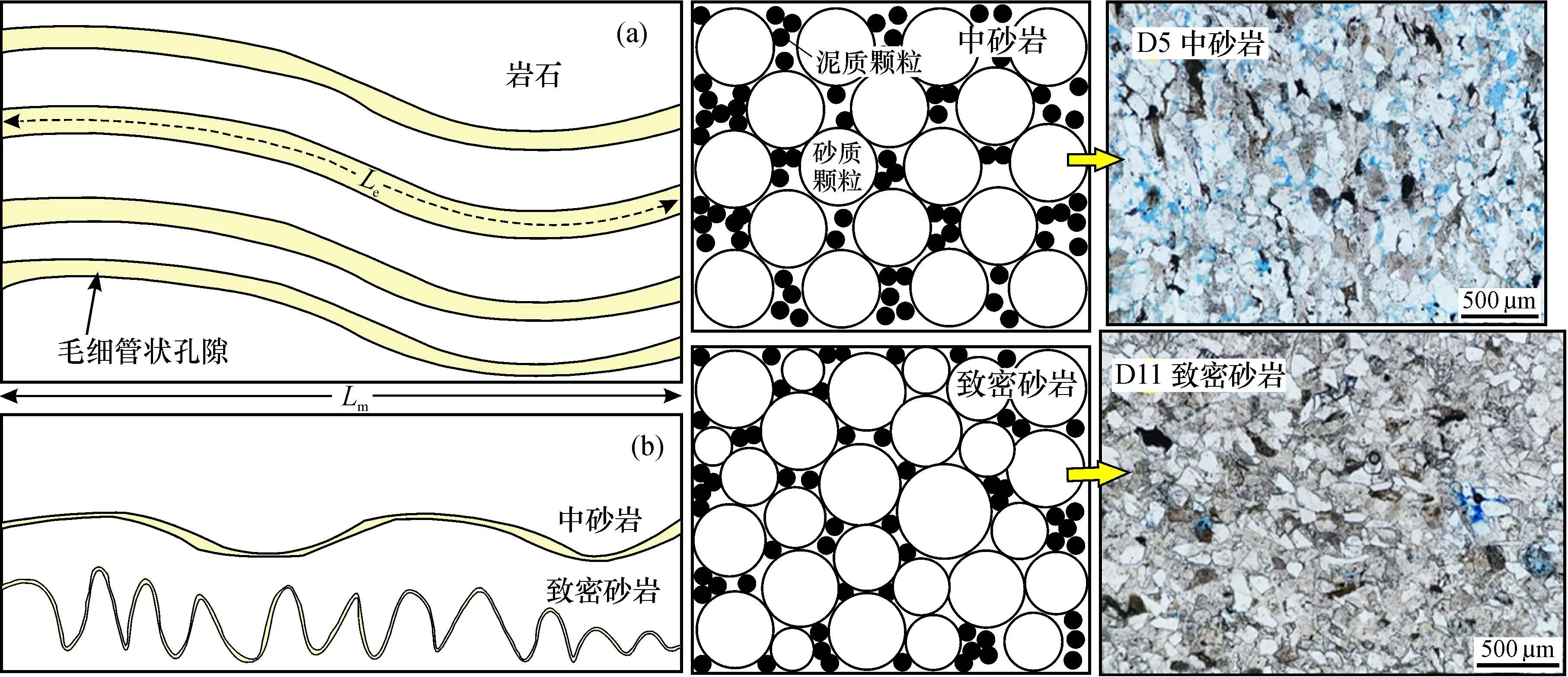
图7 不同类型砂岩的理论毛管路径及孔隙排列模型Fig.7 Theoretical capillary path and pore arrangement model for different types of sandstonesa—岩石中弯曲毛管;b—不同类型砂岩等效毛管迂曲度模型
3.4 渗透率估算及讨论
根据上述研究可知,利用分形理论可以解释不同类型砂岩渗透率的差别。因此,本文同时探讨了利用分形维值计算致密油储层渗透率的预测结果。文献[22]推导出了利用分形原理计算岩石渗透率的详细方法,给出了岩石渗透率的表达方程
(16)
式中:β为常数项,当岩石中的孔隙为球体时,β取4π/3; 而当岩石中的孔隙为立方体时,β取1。 本文取致密油储层的β=4π/3。 在利用式(16)完成计算后,岩石渗透率计算结果与实测值之间存在一个系统误差,需要利用式(17)进行校正:
y=34.4x0.764。
(17)
利用上述校正方程对各组砂岩岩样的渗透率预测结果进行校正后,各样品的最终预测结果与实测值之间的对比结果见图8。从渗透率预测结果来看,无论是中等物性的中砂岩,还是低孔低渗的致密砂岩,其预测效果均非常好。这表明利用分形理论模型预测致密油储层渗透率是有效的。从另一方面也表明,前述分析结论及所建立的模型是可靠的。
本文主要利用分形理论模型探讨了致密油储层的内部孔隙结构(主要为毛细管迂曲度)特征。而利用分形理论计算的渗透率与致密油储层实际渗透率是非常一致的,其从另外一个角度证明了利用微观孔隙分形参数评价的致密油储层孔隙结构特征是合理的。同时,所求取的分形参数或利用分形模型计算的渗透率与储层实际渗透率均具有良好的相关性,表明致密油储层渗透率与岩石的分形维数或毛细管迂曲度具有直接联系。通过压汞数据可以求取DT来判断毛细管迂曲度特征,该参数可以作为致密油储层评价或建模的基础指标。
虽然压汞实验成本较高,但压汞测试是致密油储层评价及分级中的必测项,因此,结合压汞测试可以对致密油储层分形性及孔隙微观结构特征进行评价。同时,该研究可以为致密油储层的渗透率评价提供一些新的思路。对于研究区渗透率极低的致密油储层段,当实验测试的渗透率可靠性存在疑问时,还可以基于获得的分形维数或本文校正后的渗透率计算模型进行预测。

图8 利用分形理论模型估算岩样的渗透率结果Fig.8 Estimation of permeability of rock samples using fractal theory model
4 结 论
(1) 本文以鄂尔多斯盆地定边油田延长组长7致密油储层为例,利用高压压汞实验和分形原理分析了目的层砂岩的分形特征。研究结果表明,砂岩样品的分形维数(Df)分布在2.759~2.987,平均值为2.890; 毛细管平均迂曲度分维值(DT)分布在1.194~1.553,平均值为1.391,Df>DT。
(2) 测试岩样的Df与DT与渗透率间均存在较好的负相关性。 致密砂岩的Df和DT值要大于中砂岩,表明与中砂岩相比,致密砂岩内部微孔的分布较为杂乱,孔隙间的连通性差,且其毛细管迂曲度较大。 因此,致密砂岩中流体渗流所需通过的路径更长,这是造成其渗透率低的重要原因。
(3) 利用分形理论模型对砂岩岩样的渗透率进行了预测,预测效果非常好,表明利用分形理论预测致密油储层渗透率是有效的。本文所取得的认识对更深入探讨致密油储层岩石微观渗流机理方面具有重要的参考价值。

