平行四边形中的考点分析
徐聪


平行四边形是初中数学中最重要的基本图形之一,是学习和研究特殊四边形的基础。它的概念、性质和判定,是中考重点考查的内容,考查形式也丰富多样。
一、夯实基础是根本
教材中给出了平行四边形的定义和三种判定方法,都是从四边形的边、角、对角线中选取恰当的条件得到平行四边形,但也有一些组合是不能推出四边形是平行四边形的。下面以一道例题呈现。
例1 (2018·内蒙古呼和浩特)顺次连接平面上A、B、C、D四点得到一个四边形,从①AB∥CD,②BC=AD,③∠A=∠C,④∠B=∠D四个条件中任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有()。
A.5种 B.4种 C.3种 D.1种
【分析】能够识别平行四边形的有:(1)两组对边分别平行的四边形是平行四边形(定义);(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形。满足①②的条件的四边形可以是等腰梯形,但等腰梯形不是平行四边形;同理,满足②③或②④构不成平行四边形。当选①③时,四边形ABCD为平行四边形;当选①④时,四边形ABCD为平行四边形;当选③④时,四边形ABCD为平行四边形。故有3种。故选C。
【点评】教材中的基本概念、性质与判定是学习的根本和基础,只有熟练掌握了,才能灵活运用。
二、关注平行四边形的核心要素
平行四边形作为一种特殊的四边形,在边、角和对角线方面有许多性质。近年来,利用平行四边形的性质作图的考题也很常见,能熟练运用平行四边形的性质是解题的关键。
例2 (2019·江苏无锡)我们知道,三角形具有性质:三条中線相交于一点。请运用上述性质,只用直尺(不带刻度)作图。如图1,在[?]ABCD中,E为CD的中点,作BC的中点F。
【分析】研究平行四边形就是要关注其基本的要素——边、角及对角线。根据题意:已经知道了平行四边形一条边上的中点,要求另一边上的中点,自然应该联想到平行四边形的对角线的交点。若O为[?]ABCD对角线的交点,这样在△BCD中就有了BD边和CD边的中点,连接两条中线BE、CO得交点M,根据“三角形的三条中线相交于一点”可知BC边上的中线一定过点M,所以再连接DM并延长,与线段BC的交点即为所求。
解:连接AC、BD交于点O,连接EB交AC于点M,连接DM并延长交BC于点F,F即为所求,如图2。
【点评】平行四边形的识别、性质与应用是近年来中考的热门问题,如能正确运用平行四边形的性质、判定以及转化等数学思想,解题会变得容易上手。
三、思考问题要全面
例3 (2019·云南)在[?]ABCD中,∠A=30°,AD=4[3],BD=4,则[?]ABCD的面积等于 。
【分析】画出符合条件的草图,不难发现,符合条件的平行四边形的边AB有两种情况。本题涉及九年级内容,同学们仅作了解即可。
解:过点D作DE⊥AB于E,∵∠A=30°,∴DE=2[3],AE=6。在Rt△DBE中,BE=[BD2-DE2]=2,∴AB=AE+BE=8,或AB=AE-BE=4,∴平行四边形ABCD的面积为8×2[3]=16[3]或4×2[3]=8[3]。故答案为8[3]或16[3] 。
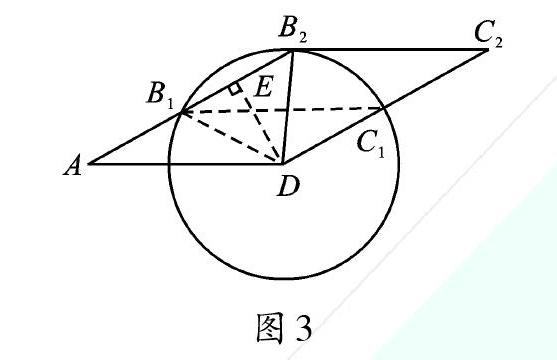
【点评】由题中给出的∠A=30°,AD=4[3],BD=4可以看出,在△ABD中,两条边和一个角是按照“SSA”的顺序给定的,这样的三角形可能不是唯一的,△ABD存在两种可能,因此[?]ABCD也有两种情况。如图3所示,点B落在以D点为圆心、DB为半径的圆上。
四、注重知识间的联系
解:若线段AB为平行四边形的边,则OC和AB平行且相等,由点A和点B的坐标可知,将点A先向右平移1个单位长度,再向上平移两个单位长度即可得到点B,所以点O和点C之间一定也是这种平移方式。如果是点O到点C按此方式平移,可得点C1坐标为(1,2);相反,如果是点C到点O按这种方式平移,则将点O向反方向移动即可得到点C2(-1,-2),从图4到图5所示。若线段AB为对角线,则线段OC也是平行四边形的对角线,并且具有相同的中点。从点O到点A,可知点C3的纵坐标不变,横坐标为4+3,因此点C3坐标为(7,2),如图6所示。综上所述,点C坐标为(1,2),(-1,-2),(7,2)。
【点评】利用平行四边形的性质,可以快速得到第四个点的坐标。这种方法同样适用于菱形、矩形、正方形存在性的探讨。随着日后学习的深入,当平行四边形与其他问题相结合时,越发可以显示它的“威力”。
(作者单位:江苏省无锡金桥双语实验学校)
——书写要点(三)

