基于BSO-BP神经网络的赤潮预测模型

胡泽民 刘致宏

1 桂林电子科技大学 商学院，广西 桂林 541004；2 桂林航天工业学院 校长办公室，广西 桂林 541004；3 桂林电子科技大学 北海校区，广西 北海 536005

赤潮又称为有害藻华(Harmful Algal Blooms，HABs)，是指微藻、原生动物或细菌在适宜的海洋环境中大量的繁殖、聚集，从而导致海水局部变色的一种现象[1]。近几年，随着我国人口的迅速增长以及现代工业化的不断发展扩大，大量未经处理的生活污水以及工业废水排放到近岸海域，导致海水富营养化，为赤潮生物繁殖提供了物质基础[2]。根据国家海洋局2013-2017年发布的《中国海洋灾害公报》统计[3]，2013年赤潮发生次数46次，2017年上升到68次，我国赤潮灾害发生次数总体呈现出上升的趋势。因此，对赤潮灾害进行预测对保护海洋生态环境具有重大的意义。

赤潮形成的机制非常复杂，目前还没有统一的结论[4-5]。随着人工智能技术的发展，国内外学者开始将数据驱动模型应用于赤潮预测研究中。苏新红等[6]应用BP神经网络建立了赤潮等级与气温、降水、风速、气压和日照等气象因子的非线性关系模型，预测准确率达到70%～80%。BP神经网络强大的非线性拟合能力对赤潮灾害预测具有较好的预测效果。但是，BP神经网络存在容易陷入局部最优的缺陷。针对BP神经网络存在的缺陷，许多学者将智能优化算法与BP神经网络结合。Yaoming Zhou等[7]分别用遗传算法GA以及粒子群算法PSO优化BP神经网络。结果表明PSO-BP、GA-BP模型相对于BP神经网络预测的精度更高。Gao F等[8]建立PSO-BP模型对叶绿素a浓度进行预测，提高了预测精度。遗传算法虽然能够对问题解进行全局搜索，但是计算复杂，收敛缓慢。粒子群算法寻优速度快，但是易发散。天牛须搜索算法(Beetle Antennae Search, BAS)BAS类似于PSO以及GA等智能优化算法，具有收敛速度快的特性。但是，BAS算法是单体智能优化算法，在处理高维数据时易陷入局部最优。因此，本文将粒子群和BAS算法结合，提出一种倒S型函数的BSO-BP的赤潮预测模型。通过在MATLAB仿真软件上对比BP、PSO-BP、BAS-BP等模型，验证了BSO-BP模型的可靠性，为赤潮灾害预测提出了一种可供参考的新方法。

1 BSO-BP模型描述

1.1 BP神经网络

BP(Back Propagation)神经网络是一种典型的前馈神经网络，由输入层、隐含层以及输出层组成[9]。BP神经网络结构图如图1所示。

图1 BP神经网络结构

其原理是通过梯度下降法，利用误差反向传播不断调整权值、阈值，直到误差达到设定的精度标准或者满足迭代的次数。BP神经网络包含信息前向传递以及误差反向传播两个阶段[10]。在信息前向传递阶段，输入数据通过权值、阈值融合计算，再通过隐含层激活函数变化得到相应的输出数据。将输出数据对应下一层的输入数据，再进行相应的计算，得到最后的输出结果。误差反向传播阶段将输出的结果与真实值进行对比，并将误差反向传递到上一层，根据梯度值来调整权值、阈值，直到达到迭代终止条件。

1.2 BAS算法

BAS算法[11-14]是2017年依据天牛觅食原理提出的一种生物启发式智能优化算法。天牛觅食原理为：天牛在不知道食物具体位置时，根据头上的两只触角来判定食物的位置。当右边触角接收到的食物气味强度更大的时候，天牛会向右方向移动。反之，则会向左方向移动。依据这一简单的觅食原理，天牛最终会找到食物。BAS寻优步骤如下。

(1)初始化天牛须朝向，生成一个n维的随机空间向量。

(1)

(2)生成天牛左右须的空间位置。

(2)

(3)

(3)根据适应度函数计算出天牛左右须的适应度值，即天牛须感应到的食物气味强度。

(4)根据适应度函数值的大小，更新天牛质心的位置。

(4)

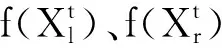
1.3 天牛群优化算法(BSO)

天牛群优化算法(Beetle Swarm Optimization Algorithm，BSO)是天牛须BAS与粒子群PSO算法的结合[15]。BAS算法是一种单体智能优化算法，在处理高维数据时，容易陷入局部最优。因此，将BAS算法和PSO算法结合，扩展为天牛群智能优化算法。BSO算法保留了天牛觅食的原理，同时引入了粒子群群体信息共享的机制，将PSO算法中的粒子用天牛代替。

(5)

(6)

天牛群位置以及速度更新公式如下：

(7)

(8)

在标准的PSO算法中，惯性权重通常是一个固定的值。研究表明惯性权重ω对粒子的搜索范围有很大的影响[16]。当ω取较大值时，全局搜索能力较强。当ω取较小值时，局部搜索能力较强，有利于后期提高收敛精度。为了让天牛在前期进行全局搜索，后期进行局部搜索。本文引入倒S型函数对惯性权重进行调整。惯性权重更新公式如下：

(9)

式中，a=5、b=0.2；ω最大值取0.9、最小值取0.4。

惯性权重ω曲线图如下。

图2 惯性权重曲线图

由图2可以看出，倒S型递减函数相对于线性递减函数，在前期变化缓慢，有利于天牛群前期进行全局搜索。线性惯性权重前期衰减太快，容易失去种群多样性。倒S型递减函数在中、后期下降迅速，使得天牛群进行局部搜索，提升收敛精度，加快收敛速度。

2 赤潮预测实现过程

赤潮预测模型主要分为三部分：首先，利用KPCA对原始赤潮样本数据进行降维，加快网络的收敛速度。其次，通过BSO算法寻找BP神经网络最佳的初始权值、阈值。最后，将BSO找到的最优解赋给BP神经网络的初始化权值、阈值。具体步骤如图3所示。

图3 赤潮预测实现过程

2.1 KPCA数据预处理

核主成分分析法(Kernel Principal Component Analysis，KPCA)是一种实现高维变量数据降维的非线性主元分析方法[17]，其原理是将输入数据样本映射到高维特征空间中，再利用主成分分析法PCA对高维特征空间中的数据进行线性降维[18]。KPCA通过损失少量的数据信息达到降低数据维度的目的。具体步骤如下[19]。

(1)将输入数据标准化处理。

(10)

(11)

(2)通过高斯核函数计算出核矩阵。

(12)

(3)中心化核矩阵K，使得核矩阵更加聚集。

K′=K-InK-KIn+InKIn，

(13)

式中：In是一个所有值均为1/n的n×n维矩阵。

(4)计算出特征值和特征向量。

(5)将各特征值除以总特征值之和，得出贡献率。

根据上述步骤，设置累计贡献率为90%，完成原始数据降维处理，得出累计贡献率超过90%的主成分。结果如图4所示。特征值以及累计贡献率如表1所示。

图4 核主成分分析图

表1 各核主成分特征值及贡献率

根据表1可知，前4个主元的贡献率为90.924%。超过了设定的阈值90%。因此，选取前4个主元作为BSO-BP的输入数据。

2.2 BSO-BP赤潮预测模型

BP神经网络基于梯度下降法且随机初始权值容易导致网络不稳定、易陷入局部最优。将BSO全局搜索特性结合BP神经网络，从而避免BP神经网络易陷入局部最优的情况。具体步骤如下。

(1)将KPCA降维后的数据作为BSO-BP神经网络的输入样本。

(2)初始化天牛群参数。设置天牛群规模n、最大迭代次数t、惯性权重ω以及搜索空间维度k等。搜索空间维度的计算公式如下：

k=i·h+o·h+h+o，

(14)

式中：i表示输入层神经元个数；h表示隐含层神经元个数；o表示输出层神经元个数。

(3)种群初始化。随机生成天牛位置、速度。根据式(15)计算出适应度函数值，保存天牛个体极值以及群体极值。并根据式(16)，更新天牛步长δt。

(15)

δt+1=eta·δt，

(16)

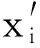
(4)迭代寻优。根据式(7)～(9),分别对天牛位置、速度以及惯性权重进行更新。计算各天牛位置的适应度值，通过与历史个体极值与历史群体极值相比较，更新天牛群体的个体极值和群体极值。

(5)当迭代次数达到设定的值时，将BSO寻找到的最优解赋给BP神经网络的初始权值、阈值。

(6)训练BP神经网络模型。计算误差，通过误差反向传播不断更新网络权值、阈值，直到达到设定的精度或者满足迭代的最大次数。

(7)将训练好的网络模型输出预测值，并将结果以可视化的方式呈现出来。

3 仿真过程和结果分析

本文所采用的赤潮分析样本数据来源于石家岛附近海域所观测到的28组夜光藻密度数据以及各种环境理化因子数据[20]，具体数据如表2所示。目前，一般认为海水富营养化是赤潮发生的首要条件，水文参数以及各种理化因子是赤潮发生的重要原因[21]。因此，本文选取水温、溶解氧浓度、盐度、总氮、可溶性无机磷以及浮游植物密度等与赤潮发生的强相关因子作为原始样本数据。选取样本7、14、21、28作为测试样本，验证BP神经网络的泛化能力。其余的样本作为训练集用来训练神经网络。仿真实验平台为MATLAB 2016a。

输入变量因单位不一致使得数据差距过大，可能导致预测误差增大。所以在训练神经网络之前，先对数据进行归一化处理，将数据映射到[-1,1]的区间上。归一化公式如下：

(17)

表2 赤潮样本数据[20]

3.1 模型性能评价方法

本文选取平均相对误差(Average Relative Error，ARE)和决定系数(Coefficient of determination，R2)来验证模型的预测性能。ARE越接近0表示预测的误差越小，模型的预测能力越强。R2的取值范围在[0,1]之间，R2越接近1，表明预测的效果越好。计算公式如下：

(18)

(19)

3.2 参数选取

BP神经网络隐含层对网络性能影响较大，通常三层的神经网络就可以达到很高的准确率。本文选取一层隐含层，隐含层个数依据式(20)选取。

(20)

式中：i表示输入层神经元个数；o表示输出层神经元个数；c是一个取值范围在[1,10]之间的常数。

输入层变量包含水温、溶解氧、盐度、总氮、可溶性无机磷以及浮游植物密度6个特征参数，经过KPCA降维后保留累计贡献率超过90%的4个主元。因此，输入层神经元个数为4。输出层为夜光藻密度，输出层神经元个数为1。依据式(20)可以得出隐含层神经元个数的范围[4,13]。通过反复试验，最终确定隐含层神经元个数为9。因此，最终网络结构为4-9-1。隐含层、输出层传递函数分别选取tansig、purelin函数。训练函数选取trainlm。

3.3 结果分析

将KPCA降维后的样本数据带入到PSO-BP、BAS-BP以及BSO-BP模型中进行训练。经过50次迭代后，得到各模型适应度曲线对比图，如图5所示。BSO-BP模型在第21次迭代时收敛，找到最小适应度值0.001 2，相较于BAS-BP、PSO-BP模型找到的最佳适应度值更低。仿真结果表明BSO-BP模型具有较好的搜索效果以及收敛速度。

图5 适应度曲线对比图

将训练样本带入到BSO-BP模型中训练，得到BSO-BP模型的训练样本输出结果，如图6所示。从图6可以看出，训练样本数据与真实值基本吻合，网络模型训练结果较好。模型训练完成之后，将测试样本带入到训练好的BSO-BP模型中，输出夜光藻密度值，如图7所示。由图7可以看出，BSO-BP预测值与实际值较为拟合，具有较好的泛化能力。

图6 BSO-BP训练样本拟合结果

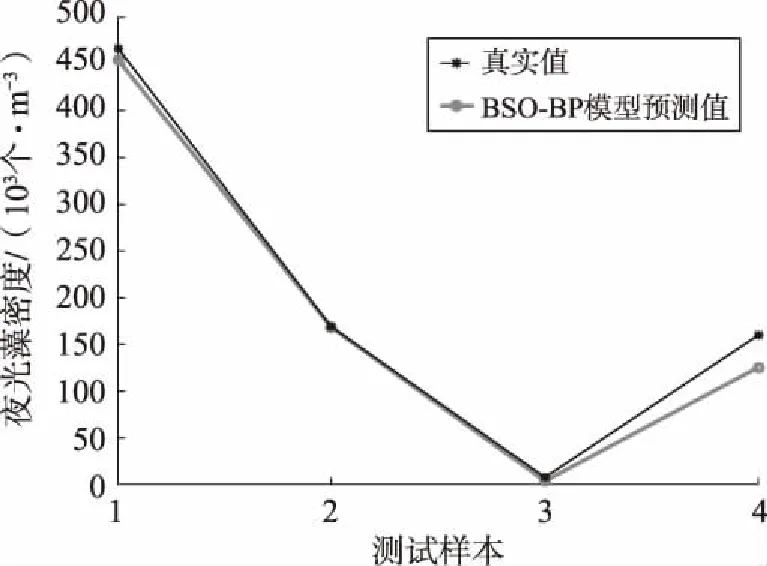
图7 BSO-BP测试样本输出结果

为了进一步验证BSO-BP网络模型在赤潮预测中的性能，分别与BP、PSO-BP以及BAS-BP等模型的预测结果进行对比。结果如图8所示。

图8 不同模型结果对比

从图8可以看出，BP神经网络在各个预测点的误差相对较大；PSO-BP模型在第3个预测点与真实值最为接近，第2个点误差最大；BAS-BP模型的第1个预测点与真实值最为接近，第3个点的预测值误差较大。BSO-BP模型在第2个点预测效果最好，第3个预测点误差较大；从整体上看，BSO-BP模型的预测值与真实值更加拟合，整体的预测效果更好。不同模型在相对误差RE、平均相对误差ARE、决定系数R2的数据对比如表3、表4所示。

表3各模型预测结果

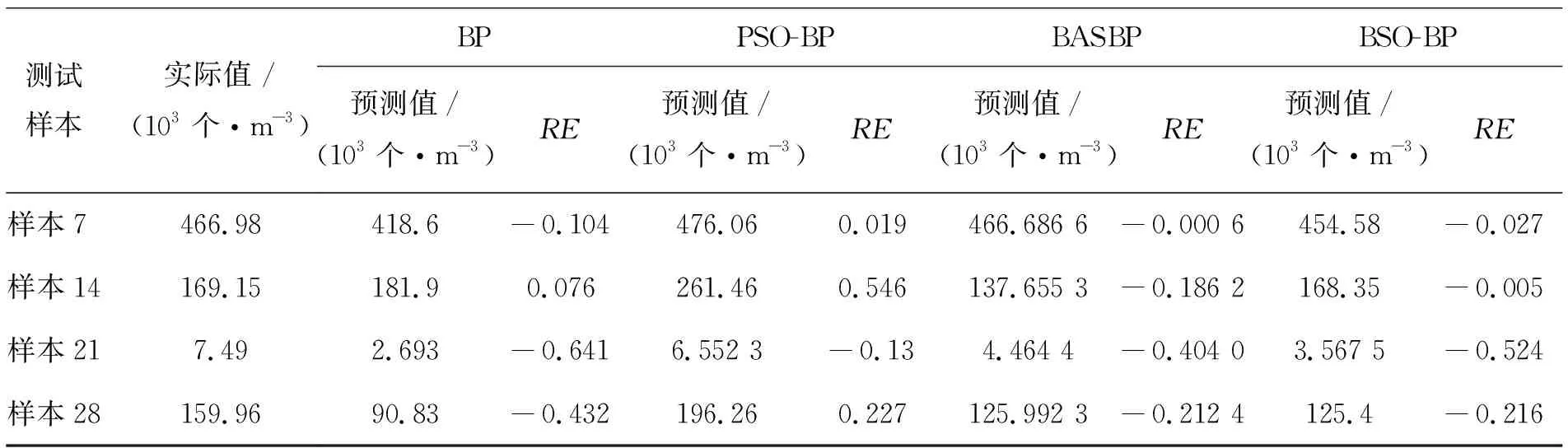
测试样本实际值 /(103个·m-3)BPPSO-BPBAS-BPBSO-BP预测值/ (103个·m-3)RE预测值/ (103个·m-3) RE预测值/(103个·m-3)RE预测值/ (103个·m-3) RE样本7466.98418.6-0.104476.060.019466.686 6-0.000 6454.58-0.027样本14169.15181.90.076261.460.546137.655 3-0.186 2168.35-0.005样本217.492.693-0.6416.552 3-0.134.464 4-0.404 03.567 5-0.524样本28159.9690.83-0.432196.260.227125.992 3-0.212 4125.4-0.216

表4 各模型性能对比

平均相对误差ARE越小，代表模型预测的夜光藻密度与实际值更为接近。决定系数R2越接近1表示预测值与输出值拟合效果越好。通过表3、表4可以看出，BP神经网络模型的平均相对误差最大。说明BP模型相对于其他优化模型预测误差更大，容易陷入局部最优。经过PSO、BAS以及BSO算法优化后的BP神经网络，有效地降低了预测的平均相对误差。BSO-BP相对于BAS-BP以及PSO-BP的平均相对误差更小并且BSO-BP模型的决定系数更接近1，预测曲线与实际值更加拟合。综上所述，BSO-BP模型相对于其他模型在预测精度上具有优势，对夜光藻密度预测效果更好。

4 结束语

本文通过KPCA对输入变量进行降维分析，提取出包含原始信息90.924%的4个主元。从而减少输入向量的维度，加快模型的收敛速度。其次，在BAS算法的基础上结合PSO群体信息共享机制，提出一种倒S型函数的BSO-BP模型。利用BSO优化BP神经网络的初始权值、阈值。结果表明BSO寻优后找到的权值、阈值明显比BP神经网络随机权值、阈值预测效果要好。相对于其他优化算法，BSO-BP在预测精度上具有优势并且具有更好的非线性拟合效果。

本文通过BP模型的BSO优化算法，为赤潮灾害的预测提出了一个可供参考的新方法。虽然BSO-BP预测效果相较于其他模型有一定的优势。但也存在许多改进的空间。BSO模型参数较多，需要对参数进行多次调整，反复实验。因此，如何减少BSO模型的参数，加快收敛速度是下一步研究的问题。