遵循生长规律 找寻解题策略

合肥市程龙军名师工作室 经开区名师工作室/

合肥一六八玫瑰园学校教育集团/ 李岩

卜以楼老师的生长数学观认为：教学的首要任务,就是要明晰“教什么”的问题。“教什么”是指“教学生学什么”和“教学生怎么学”。如果说教师教什么,学生就得听什么,那么教师的主导地位与学生的主体地位的关系就不明确,很容易变成以教师为主宰。教师把“学生学什么”作为教的内容,那关系就比较明确了,教师要教学生的是“学什么”,就是引导学生去质疑、去发现、去探究、去归纳、去判断、去概括……去把本来教师要教的东西变为学生自己去探索他所应该学的东西。本文以上述“生长数学”的观点谈谈一道中考试题的教学。

一、试题呈现

已知： 在矩形ABCD 中，BD 是对角线，AE⊥BD于点E，CF⊥BD 于点F，如图1。

（1） 求证：AE=CF；

（2） 如图2，当∠ADB=30°时，连接AF、CE，在不添加任何辅助线的情况下,请直接写出图2 中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的。

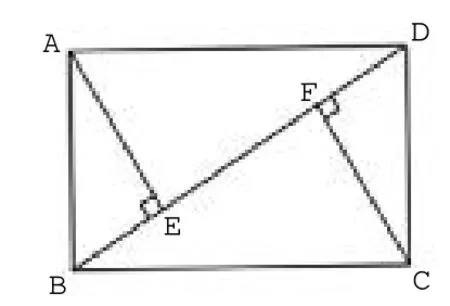
图1

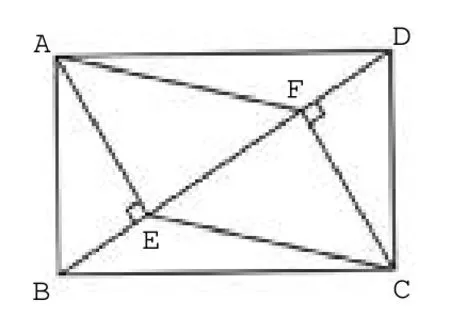
图2

二、学生解决问题情况反馈

本题是2019 年黑龙江省哈尔滨市的一道中考试题。第（1）题是证明两条线段相等，可利用全等三角形进行证明。通过对学生解题情况的观察发现，学生选择哪一对三角形以及证明这一对三角形全等的条件的选择都具有多样性，而且都能较为顺利地解决。第（2）题需要根据图形和题意直接写出符合条件的四个三角形。笔者在巡视指导中发现学生分析题目不够透彻，对于面积的计算找不到抓手，没有回归题目的本质从三角形的高入手思考问题，进而在直接写出结论的过程中出现拦路虎，基础稍弱的同学基本放弃了思考。即使有学生得到了结果，但基本都是通过添加辅助线而得出的。

那么，对于类似的问题，教师应该如何引导学生学会解决呢？ 这其实就是教师要明确“教什么”的问题，事实上就是指“教学生学什么”和“教学生怎么学”，这就需要教师引导学生去质疑、去发现、去探究、去归纳、去判断、去概括等，把本来需要教师教的东西变成学生自己经过探究应该获取的东西。

三、以生长数学观指导学生解决问题

生长数学的教学观是将自然生长的理念引入数学学习活动的教学，是让数学学习活动助力个体生命生长的教学，是前后一致的、逻辑连贯的、一以贯之的数学教学。在这个过程中,需要关注知识的生长、生命的生长、智慧的生长、境界的生长。回到具体问题的解决上来，教师应该教会学生干什么、怎么干、干干看和回头看。

1.干什么

可以引导学生按照以下步骤对问题进行分析。

（1） 题目要我们干什么？

第（1）问要求证明什么？第（2）问如何直接得出四个三角形？

立意：确定问题最终目的，让学生在梳理条件过程中有明确的方向。在第（2）问中要明确要求不能添加辅助线。

（2） 题目中的所给条件有哪些？

立意：梳理题目中的已知条件，哪些条件可以为我所用。对于本题，已给条件有：①四边形ABCD 是矩形；②BD 是对角线；③AE⊥BD 于点E；④CF⊥BD 于点F。第（2）问中又给出的条件是：⑤∠ADB=30°；⑥不添加任何辅助线；⑦写出的四个三角形中的每个三角形的面积都等于矩形面积的。

（3） 题目中的隐含条件又有哪些呢？

立意：题目中隐含条件的挖掘往往是解决问题的关键。本题的隐含条件有（由矩形的性质可得）：①对边相等AB=CD，AD=BC ；②对边平行AB∥CD，AD∥BC；③内错角相等∠ABE=∠CDF，∠CBE=∠ADE，等。

2.怎么干

第（1）问要求证明AE=CF，这是证明两条线段相等。目前我们证明线段相等的方法有很多，学生也非常容易想到最直接的方法就是寻找并证明两个三角形全等，而这一点并不难。问题的关键在于教师要教会学生学会深入思考，领悟第（1）问的作用，关注第（1）问和第（2）问之间的联系，第（1）问能否为第（2）问的解决提供必要的帮助。对于怎么干，路径和方向很重要。

3.干干看

当我们有了解决问题的清晰思路，抑或只是有了一点苗头，接着就应该进行大胆尝试，或许在尝试过程中，我们的思路有可能豁然开朗。

问题（1）的证明：在矩形ABCD 中，∵AB∥CD 且AB=CD，∴∠ABE=∠CDF。又∵AE⊥BD，CF⊥BD，∴∠AEB=∠CFD=90°。∵∠ABE=∠CDF，∠AEB=∠CFD=90°，AB=CD，∴△ABE≌△CDF。∴AE=CF。

对于问题（2），可以考虑两个思路。

（2） ∵S△ABE=DF·AE，且BE=DF，∴ S△ABE=S△ADF=S矩形ABCD。同理S△BCE=SS矩形ABCD。所以，四个三角形分别是△ABE，△ADF，△CBE，△CDF。

4.回头看

本题考察了矩形的性质、全等三角形、含30°角的直角三角形性质、勾股定理、等积三角形等知识，对学生的综合能力有较高的要求，“等底等高的两个三角形面积相等”是解决本题的关键。第（1）问的证明两条线段相等并不是一个孤立的问题，而是为了证明第（2）问中的两个△ABE 和△CBE 的高相等，这样四个三角形面积相等也就自然而然地得到了。至于面积如何等于原矩形面积的，则可以由含30°角的直角三角形的三边关系来确定。

从此题的解答过程中可以看出，题目本身难度不大，但得分率不高，原因在于学生在找已知条件时，不能充分挖掘题目本身的隐含条件，而本题对于隐含信息的梳理尤为重要。这就需要借助几何直观将问题变得简明与形象，以便于学生探索解决问题的策略与方法，实现数学能力的升华。

四、结束语

北京大学丘维声教授说过：“学数学就是学数学思维方式。”因此，教数学也就是教数学思维方式。思维方式既具有策略的宏观灵动，又具有方法的微观定向。对于图形问题，需要经历抽象、分析、计算、思维生长等过程，探索图形中各元素之间的关系，然后通过逻辑推理进行证明，这个过程可以让学生清晰地体会到合情推理和演绎推理的灵魂。数学核心素养的养成，不能单纯依赖教师的“教”，而是需要学生参与其中，遵循知识生长规律，寻找解决问题策略，感悟数学本质，积累解决问题的能力和经验。