大型风力发电机塔架结构的固有频率分析
王超, 崔承勋
( 延边大学 工学院, 吉林 延吉 133002 )
0 引言
传统能源如煤、石油等的大量使用,不仅给环境带来了严重污染,而且也增加了地球的“温室效应”,因此开发利用新能源具有重要意义.风能作为一种清洁的可再生能源一直受到人们的关注.近年来,随着风能技术的相对成熟,以及国家新能源政策的实施,风电已成为我国第3大发电方式[1].塔架是风力发电机(下文简称风机)的重要支撑部件,其主要功能是支撑主机中所有零部件的重量和提高叶片风能的利用率.研究表明,风轮的旋转是影响塔架振动的主要原因.另外,若风轮旋转产生的频率与塔架的固有频率接近,塔架就会产生共振现象.塔架振动和塔架与风轮产生的共振不仅会严重影响风机的稳定性,而且甚至还会导致风机倒塌,从而造成重大经济损失[2-3].因此,在风机设计阶段通过分析塔架结构的振动特性来预估塔架的固有频率,对避免塔架共振情况的发生具有重要的意义.
目前,国内外学者对塔架的振动特性做了很多研究.例如: Murtagh等[4]建立了一种叶片-塔架耦合模型,分析了塔架在随机载荷下的振动响应.张力伟等[5]建立了一种桩-土体模型,研究了在流固耦合作用时海水对模型动响应的影响,并分析了整机在El-Centro波作用下的地震动响应.张永强[6]基于Galerkin法提出了一种可以计算拉索式小型风机塔架结构固有频率的理论模型,并验证了其有效性.林炅增等[7]研究了海上风机的单桩基础,以及在畸形波作用下波浪力对风机的影响.但目前为止国内外学者对预测塔架固有频率的研究相对较少,相关文献[8-9]仅是通过模态分析对塔架的固有频率进行了预测.为此,本文以某型号750 kW大型风机为研究对象,利用Receptance法提出一种计算大型风机塔架固有频率的理论模型.
1 基于Receptance法分析塔架的固有频率
Receptance法的基本原理就是将两个连接的构件分开进行研究,因两个构件的连接处位移相同,因此可以利用该原理建立求解固有频率的方程.本文将塔架上端零部件简化成集中质量me,而对于非均匀构件,取其边界条件相同的均匀构件作为分析模型[10].由此本文中的塔架分析可简化成均匀梁分析,简化后的分析模型如图1所示.
因风机系统是按正弦规律进行运动,基于Receptance法原理首先对塔架进行研究,其中塔架顶端受力情况如图2所示.

图1 塔架简化后的分析模型

图2 塔架受力分析模型
求解连续系统的振动问题需要对系统的偏微分方程进行解耦,使联立的方程组解耦成n个独立的单自由度的微分方程.求得各个单自由度的响应后,通过模态的叠加就可得到系统的全部响应[10].故塔架的振动方程可表示为
(1)
上式中Φr(x)为悬臂梁自由振动的振型,ηr(t)为系统的广义坐标.由文献[10]可知,Φr(x)和ηr(t)的表达式分别为:
Φr(x)=C1(sinβrx-sinhβrx+ξr(cosβrx-coshβrx)),
(2)
ηr(t)=Crcos(ωrt-φr).
(3)

利用Lagrange方程求解塔架的振动方程需用到塔架势能、动能和广义力的表达式.根据动能定义,塔架的动能表达式为
(4)
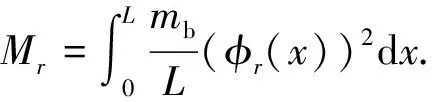
(5)
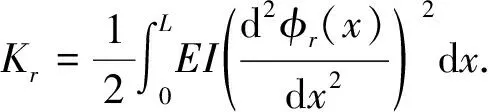

(6)
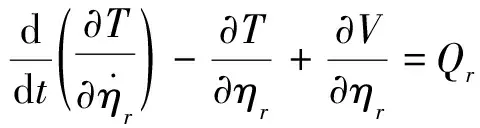
(7)
用卷积方法对式(7)进行求解,得
(8)
式中F0是简谐激励力的力幅,Φr(L)为塔架顶端的振型,ω是外界激励频率,ωr是系统的第r阶固有频率,Mr是塔架的广义质量.式(8)中第2项因是一种瞬态的自由响应,故本文只考虑第1项(稳态响应)即可.于是式(8)可变形为
(9)
其中φr(L)=C1(sinβrL-sinhβrL+ξr(cosβrL-coshβrL).将式(2)和(9)代入式(1)可得塔架的响应:
(10)
由式(10)可得到塔架顶端的响应为
(11)
下面对塔架上端的集中质量进行分析.由图2可知,集中质量和塔架上端接触处是固定的,因此二者在相互接触处所受的力是一对相互作用力.根据牛顿第二定律可得集中质量的运动方程为
(12)
式中me是简化的集中质量,y(t)是集中质量的位移.由集中质量的初始条件可得集中质量的位移为
(13)
因集中质量和塔架顶端满足系统的连续性条件,故式(11)和式(13)对应的位移相等,即
(14)
式(14)即为塔架顶端带有集中质量的固有频率方程,其中n越大,固有频率的误差越小.根据风机塔架的设计精度要求[11],本文取n=4.化简式(14)后得
(15)
式(15)是关于ω的一元8次方程,其中除ω外都是已知量,因此通过求解该方程即可算出塔架的前4个(正值)固有频率.
2 模型验证
本文以750 kW风机塔架结构为例进行验证.风机的主要参数如表1所示.
2.1 有限元分析
目前,对风机进行有限元分析主要采用两种模型:一种为简化模型,即将塔架视为圆筒形,把上部零部件(机箱、叶片等)简化为集中质量[12];另一种为接近真实的风机模型,即将机舱和叶片单独画出,把机舱简化为集中质量块,按真实的尺寸和质量建立模型[13].本文利用SolidWorks软件建立上述两种模型,然后将其导入ANASYS中进行分析.其中一阶自然模态分析结果如图3和图4所示.由图3和图4可知,模型1的一阶固有频率(0.669 Hz)虽然略低于模型2的一阶固有频率(0.654 Hz),但二者相近,由此表明简化模型是有效的.

表1 风机的主要参数

图3 模型1的一阶自然模态
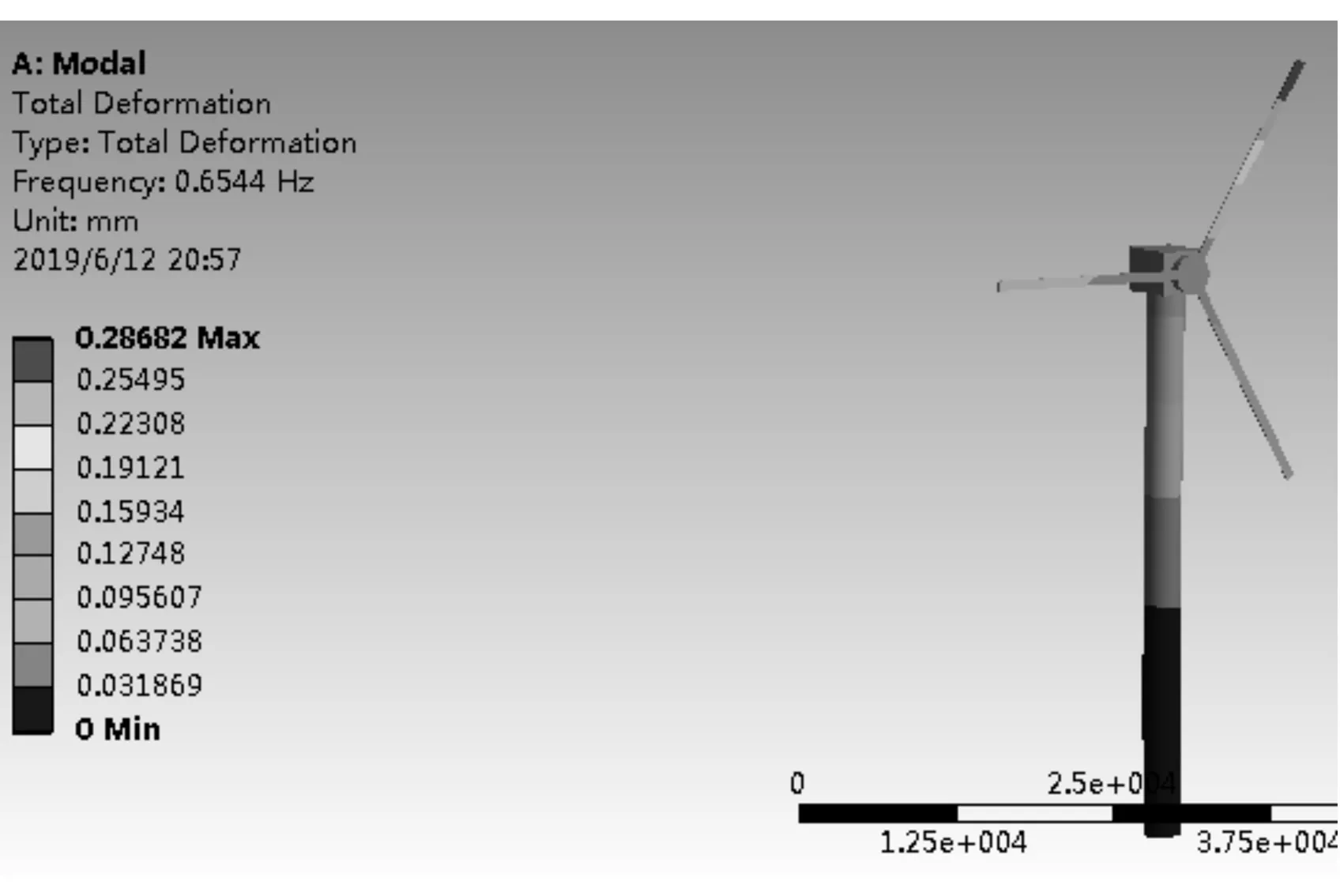
图4 模型2的一阶自然模态
2.2 实测

图5 测试时放置加速度传感器的位置
上述有限元分析得到的塔架固有频率是在理想情况下得到的,而在实际中塔架固有频率会受到各种因素的影响,如地基、风速以及螺栓的松紧程度等.为了进一步验证理论模型的有效性,本文采用振动信号测试仪对塔架的振动响应进行实际测试.因风机塔架的低阶自然模态响应主要为前后弯曲和左右摆动,故本文在不同风速下对风机塔架结构进行两个方向(X轴和Y轴)的测试,其中加速度传感器设置于离地面43.5 m处,如图5所示.
当风速为5.04 m/s、风轮转速为14.87 r/min时得到的测试结果分别如图6和图7所示.从图6(a)可以看出,在整个测试时间(0~100 s)内,由振动引起的加速度在X轴方向的变化范围为±0.03g.从图6(b)可以看出,由振动引起的加速度在0.72~0.76 Hz内存在波峰,且峰值不超过0.014g.另外,在峰值的右侧,随着频率的增加加速度逼近于0.这说明系统的一阶固有频率在0.72~0.76 Hz范围内.由图7(a)可以看出,在整个测试时间(0~100 s)内,由振动引起的加速度在Y轴方向的变化范围为±0.04g.从图7(b)可以看出,由振动引起的加速度在0.72~0.76 Hz内存在波峰,且峰值不超过0.014g.另外,在峰值的右侧,随着频率的增加加速度也逼近于0.这进一步说明系统的一阶固有频率在0.72~0.76 Hz范围内.
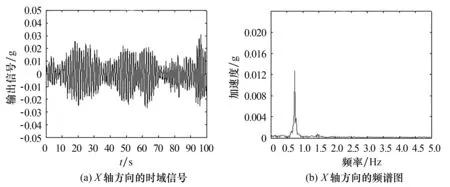
图6 X轴方向的振动信号分析

图7 Y轴方向的振动信号分析
利用Matlab软件对采集到的振动数据进行分析,结果如图8所示.从图8可以看出,无论是X轴方向还是Y轴方向,对于不同转速振动的加速度峰值始终在0.72~0.76 Hz之间,且当转速为14.8 r/min时,振动最大(发生共振).由此可判定系统的固有频率在0.72~0.76 Hz之间,因此在设计时应避免塔架固有频率出现在此范围内.
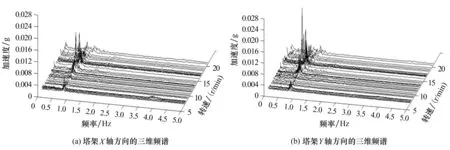
图8 不同风速下塔架的三维频谱
3 对比分析
研究[14]表明,在塔架振动过程中一阶模态的振动起主导作用,二阶模态的固有频率远大于风叶的通过频率,高阶模态在振动过程中因塔架本身所具有的阻尼作用使其衰减较快;所以,系统的整体响应可不考虑高阶模态,只分析一阶固有频率即可.对塔架进行理论分析和有限元分析所得的一阶固有频率如表2所示.由表2并结合图8可知, 3种方法得到的一阶固有频率接近,因此说明本文提出的理论模型是有效的.

表2 两种分析方法所得的一阶固有频率 Hz
4 结论
本文基于Receptance法建立了一种预测大型风机塔架固有频率的理论模型,并结合有限元分析和实际测试对其进行了验证.结果显示3种方法获得的固有频率相近,表明本文的理论模型可应用于预测塔架的一阶固有频率.本文在研究时将塔架简化成均匀悬臂梁结构,其计算结果与实际情况会有一定的误差,因此在今后的研究中我们将尝试采用半解析等方法来提高本文的预测精度.

