量子点-表面等离子波导耦合系统中的双带单向无反射现象
邹鑫宇, 张英俏
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
表面等离子激元是光与金属表面自由振动的电子相互作用而产生的沿着金属表面传播的一种电磁波模式,由于其能够突破衍射极限,在纳米尺度内可操纵光且易集成,因此常代替光子作为信息的载体[1].近年来,许多学者对发射器与波导耦合系统中单方向入射的表面等离子激元的特性进行了研究.例如: 2007年, Chang等[2]研究了纳米线中的单个表面等离子激元与1个二能级发射器构成的耦合系统中表面等离子激元的传输特性.2011年, Chen等[3]研究了金属纳米线中表面等离子激元与2个量子点耦合系统中表面等离子激元的散射性质,并通过求解本征值方程得到了该表面等离激元的透射率和反射率.2012年, Cheng等[4]在一维波导与2个半导体量子点耦合的非厄米系统中实现了Fano型透射,该成果可应用于研究生物传感器.2013年, Jin等[5]研究了折射率接近于零的表面等离子波导中两个量子点之间的量子纠缠和散射特性.2015年, Kim等[6]分别研究了3个不等间距的二能级量子点与一维波导耦合的系统,以及1个二能级量子点和1个V型三能级量子点与一维波导耦合系统的散射性质,发现只要二能级量子点和V型三能级量子点的间距与3个二能级量子点的间距相等,就能得到完全相同的表面等离子激元的透射光谱.同年, Kim等[7]还研究了一维波导与2个Λ型三能级量子点相互作用的系统表面等离子激元的散射特性,通过控制经典驱动场并调节量子点与腔之间的耦合强度实现了单光子开关.目前,对于双方向入射的表面等离子的传输研究相对较少.例如: 2018年, Wu等[8]在多个量子点与表面等离子激元耦合的波导系统中研究了单带和双带单向无反射; 2019年, Qiu等分别研究了2个损耗等离子激元腔[9]、1个增益和1个损耗等离子激元腔[10]耦合于等离子波导系统的单带和双带单向无反射现象.基于以上研究,本文提出一个在2个V型三能级量子点与表面等离子波导耦合的非厄米系统中获得表面等离子激元的双带单向无反射方案.
1 模型与计算
2个V型三能级量子点与表面等离子波导耦合的非厄米系统如图1所示.

图1 2个V型三能级量子点与表面等离子波导耦合系统的示意图
该系统的哈密顿(ħ=1)可以表示为
(1)
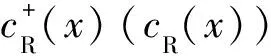
e1|0,2,1〉+e2|0,3,1〉+e3|0,1,2〉+e4|0,1,3〉.
(2)
其中: |0,1,1〉表示波导中没有表面等离子激元且2个量子点处于基态;e1、e2和e3、e4分别表示量子点1和量子点2吸收1个表面等离子激元后跃迁到激发态的概率振幅.当单个表面等离子激元沿向前或向后方向入射时,散射振幅φk,R(x)和φk,L(x)[11-12]可以分别表示为:
φk,R(x)=exp(ikx)[θ(-x)+aθ(x)θ(d-x)+tθ(x-d)],
φk,L(x)=exp(-ikx)[rθ(-x)+bθ(x)θ(d-x)].
(3)
其中:t和r分别表示表面等离子激元的透射和反射系数;θ(x)是单位阶梯函数,当x≥0或x<0时,单位阶梯函数分别等于1或0.求解本征值方程H|Ek〉=Ek|Ek〉可分别得到透射系数和向前方向、向后方向的反射系数:
(4)

2 分析与讨论
图2为相位θ=0.954 π时, 透射率和反射率随波长变化的关系.图2中的实线、虚线和点线分别对应于透射率、向前方向和向后方向的反射率.
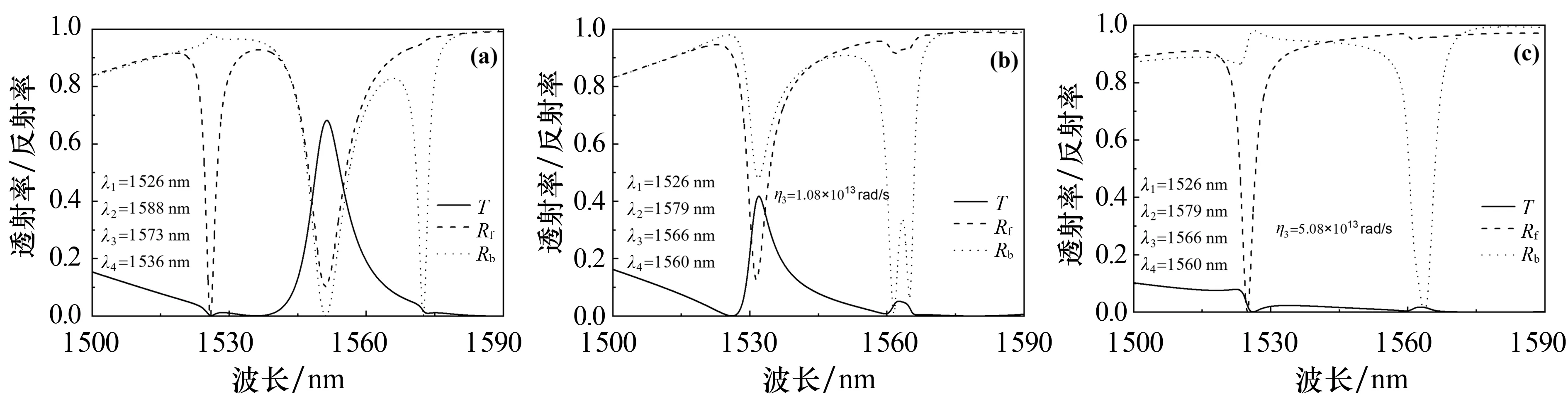
图2 θ=0.954 π时,透射率和反射率随波长的变化
图2(a)为2个量子点的共振波长分别为1 526 nm(λ1)、1 588 nm(λ2)、1 573 nm(λ3)、1 536 nm(λ4)的光谱图,其中量子点与表面等离子波导之间的耦合强度分别为η1=1.15×1013rad/s,η2=2.5×1013rad/s和η3=1.08×1013rad/s,η4=1.2×1013rad/s.由图2(a)可以看出,在波长1 526、1 551、1 573 nm处,其向前方向的反射率达到0、0.11、0.94,向后方向的反射率达到0.97、0、0,即在波长1 526、1 551 nm和1 573 nm处出现了三带单向无反射现象.
图2(b)为共振波长分别为1 526 nm(λ1)、1 579 nm(λ2)、1 566 nm(λ3)、1 560 nm(λ4)时的光谱图(其他参数不变),其中量子点与表面等离子波导之间的耦合强度分别为η1=1.15×1013rad/s,η2=2.5×1013rad/s和η3=1.08×1013rad/s,η4=1.2×1013rad/s.由图2(b)可以看出,低频处向后方向反射的2个光谱谷间距变小.
图2(c)为η3=5.8×1013rad/s时的光谱图(η1,η2,η4不变).由图2(c)可以看出,低频处向后方向的2个低反射谷合并在一起且波带变宽,表明此时出现了单向无反射现象.在波长1 526 nm (1 563 nm)处,光谱向前(向后)方向的反射率达到0(0);在波长1 526 nm (1 563 nm)处,光谱向后(向前)方向的反射率达到0.88(0.95).这表明当相位θ=0.954 π时,在1 526 nm处系统出现了窄波段单向无反射现象,在1 563 nm处系统出现了宽波段单向无反射现象.
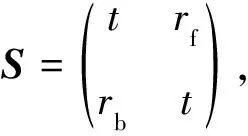
图3为相位θ=0.954 π时散射矩阵S的本征值λ±的实部和虚部随波长的变化曲线.图中的实线和虚线分别对应于本征值λ+和λ-.由图3可以看出, 2个实部与2个虚部合并并分别交叉于波长1 526 nm和1 563 nm处.由此可知,当相位θ=0.954 π时,系统在2个异常点处出现了双带单向无反射现象.

图3 θ=0.954 π时,本征值(实部和虚部)随波长的变化
图4为向前和向后方向的反射随相位和波长的变化情况.图4中2个量子点的共振波长分别为λ1=1 526 nm,λ2=1 579 nm和λ3=1 566 nm ,λ4=1 560 nm,量子点与表面等离子波导之间的耦合强度分别为η1=1.15×1013rad/s,η2=2.5×1013rad/s和η3=5.08×1013rad/s,η4=1.2×1013rad/s, 量子点的衰减率分别为Γ1=0.043η1,Γ2=0.011η2和Γ3=0.125η3,Γ4=0.15η4.由图4(a)可以看出,向前方向反射的低反射区域出现在1 521~1 529 nm波长范围内,此范围对应于图4(b)中的高反射区域.由图4(b)可以看出,向后方向反射的低反射区域出现在1 530~1 537 nm和1 560~1 571 nm波长范围内,该范围对应于图4(a)中的高反射区域.由此可知,该双带单向无反射现象能够在较宽的波长范围内出现.

图4 向前和向后方向的反射随相位和入射波长的变化
3 结论
在2个V型三能级量子点与表面等离子波导耦合的系统中,本文通过适当地调节2个量子点的共振波长、量子点和表面等离子波导之间的耦合强度,在系统的异常点(1 526 nm和1 563 nm)处实现了双带单向无反射.研究表明:在波长1 526 nm处,向前(向后)方向的反射达到0(0.88); 在波长1 563 nm处,向前(向后)方向的反射达到0.95(0);当量子点共振波长取适当的值时,增大量子点的部分能级与等离子波导之间的耦合强度,可使表面等离子激元向后方向的低频反射光谱变宽.以上结果可为研究外加经典场条件下的量子点-表面等离子波导耦合系统的等离子激元的传输性质拓宽思路,同时还可为双带滤波器、传感器、等离子开关等量子器件的研究提供理论参考.

