基于强化学习的联保贷款模式优化博弈分析

夏佳佳，王守龙

(安徽商贸职业技术学院 财务金融系，安徽 芜湖 241002)

联保贷款最初是由尤努斯为了扶持农户，帮助摆脱贫困提出的一种信贷模式[1]. 在我国，由于中小企业相较于大企业资产规模偏低，对银行的业务贡献不大，且管理水平有限，产品技术含量不高，银行对其发放贷款的综合收益远小于大型企业，因此“融资难、融资贵”. 由此，联保贷款被提出，借款主体联合若干家自愿参与联保团体的企业组成联保小组，以小组名义向商业银行申请授信，由其他成员提供连带责任担保的贷款模式. 银行利用该业务模式在一定程度上规避了单个企业融资的风险，拓宽了中小企业客户渠道，缓解了“融资难”的问题，而且随着业务的深入，一些大型民营企业也在尝试利用该方式获取融资[2]. 联保贷款业务成为化解“融资难，融资贵”问题的有效路径. 但是，由于我国目前信用体系尚未健全，信息披露机制透明度不够，联保贷款业务发生的不良贷款率逐年攀升[3]，危害了我国中小企业的健康发展. 十三届二次会议政府工作报告中明确了“民营中小型企业融资难融资贵问题尚未有效缓解”，说明现有机制没有有效解决中小企业融资问题. 我国联保贷款业务模式失效的主要原因是“搭便车”现象较为严重[4]，导致企业特别是守信企业参与积极性降低，联保贷款业务模式难以继续，对我国中小企业融资甚至健康发展产生了一定冲击. 因此，构建更为合理的约束机制促使联保贷款业务的健康持续稳定发展，对解决我国中小企业的融资问题乃至稳定发展有着非常重要的意义.

1 文献综述

目前对于联保贷款业务模式的研究较多，大致从几个角度进行分析.

联保贷款企业努力水平角度 Zhang发现联保企业均违约逃债时，其努力水平低于单独贷款企业[5]. 肖斌卿分析得到联保贷款企业努力水平取决于多种因素，并与收益、联保责任有着一定的线性关系[6].

博弈角度 相关文献分析了联保贷款模式存在的问题. 戴菊贵通过设定四种假设条件，对比分析了新旧机制下联保企业收益贴现值，结果显示联保贷款业务模式的成功是在特定条件下才可以发生的，提出“不再融资”的惩罚差别机制[7]，部分解决了由事前道德风险导致的违约逃债，创新了规避违约方法. 罗安将中小企业联保贷款模式分为两个博弈阶段进行研究，即不同企业在申请联保贷款时的策略博弈和中小企业联贷小组与商业银行的策略博弈，结果显示联保业务模式的制度必须强化企业的内部约束和违约成本[8]. 但相关研究并没有充分考虑到，联保贷款参与方的决策行为并不是一成不变的，而是随时间变化不断调整，因为参与方具备自主学习的能力且容易受到其他参与方的影响，从而改变自己的策略. 因此，上述研究有一定局限性，不能完全适用现实情况.

博弈论是试图提出某种均衡，使得博弈参与各方根据对方选择的策略做出自己最优策略选择，演化博弈基于前者提出的，旨在研究博弈各方选择的策略随着时间的改变达到稳定状态的过程. 而基于强化学习的演化博弈理论则是一种有效的结合，即在博弈各方策略选择随着时间变化的过程中，充分考虑到个体决策者具备自主学习能力特性. 博弈各方策略决策过程不再是静态的，而是转变成了由个体决策者与环境交互的动态过程. 因此，基于强化学习的演化博弈理论适用于联保贷款业务模式的优化问题.

目前，部分学者将强化学习理论已经成功应用到实践中. 吴军将强化学习的演化博弈理论应用于危化品运输的选择问题，建立博弈模型，并通过算例说明路径税收政策对于运输企业选择税收路段有正向的促进作用[9]. 黄彬彬应用于对比分析农民参与农田水利管理的一般模型和进化模型，通过算例验证了新管理模式不仅可以提高博弈参与方的收益还可以提高合作频率[10]. Julien Laumonier对多代理人强化学习进化模型做了研究，并结合纳什均衡与斯塔克尔伯格均衡建立新模型，通过自行车调度问题进行分析，结果表明两种均衡结合后的新模型更有效率[11]. 但是，将联保贷款业务模式的优化问题置于强化学习演化博弈理论内进行研究则少有涉猎.

因此，本文将建立基于强化学习的联保贷款业务模式博弈模型和信用等级制度，对比分析新旧业务模式下联保企业策略选择的改变. 首先确立“人工智能+金融”的研究模式，结合人工智能算法——强化学习，将联保贷款业务模式优化的问题置于强化学习博弈体系之内，优化联保贷款业务模式. 其次，参考“不再融资”的约束联保企业的惩罚差别机制行为，提出多层次细化的约束机制. 因为“不再融资”存在“一刀切”，对于偿还程度不一的联保贷款参与企业，会挫伤参与的积极性，银行也会错失一部分业务拓展的机会.

2 联保贷款业务模式现状及博弈模型

2.1 存在问题

联保贷款小组成员一般为实力较为均衡，彼此较为熟悉、信任程度较高的中小企业. 一般情况下，如果某个成员无法到期还款，则其他成员必须为其偿本付息[12]. 虽然这种业务模式可以让授信企业做到贷前进行筛选、调查，贷中监督和贷后管理，对银行的风险审查做到有效补充. 但是业务缺陷不可忽视，如需要企业提供的材料众多，手续繁冗，监督体制不健全，以及参与方易发生策略性违约等，还有使该业务失效的最重要因素——联保企业“搭便车”的行为.

按照商业银行相关规定，参与联保的企业如果想续贷，则需要参与各方清偿所有贷款，否则将不再批准所有小组成员企业新的融资申请. 因此，在现行联保贷款业务模式下，银行只关心贷款是否按期偿还，并不在意由联保的哪些组员偿还. 只要贷款被还清，所有参与企业均可享受银行的再融资，否则均将面临断贷的风险. 这种无差别化的业务模式，造成了部分“搭便车”失信企业享受了其他守信企业由于按期偿清贷款银行提供继续再融资的红利，却没有付出任何成本，导致联保贷款传统业务模式的失效，而这种业务模式中参与方之间的博弈类似于“智猪博弈”.

2.2 联保贷款业务模式博弈模型

2.2.1 模型假设为了简化问题，假设参与联保贷款的企业为甲企业和乙企业，博弈模型要素设定如下：

1)参与方：i∈Γ，Γ=(1、2、3…n)，组成联保贷款小组的中小企业. 将参与方分为两类，一类是还款意愿较为强烈的中小企业甲，另一类是“搭便车”意愿强烈的中小企业乙，还款概率表示为P甲>P乙，并假设甲乙双方联合向商业银行申请贷款，且甲的盈利能力大于乙.

2)策略：Si=(si1，si2，si3…in). 本模型假设有两个参与方，且参与方有两种策略选择，即选择清偿贷款或不清偿，不清偿即为违约逃债.

3)收益矩阵：Ri=ri(s1，s2，s3…，sn)，i∈Γ，ri表示参与方i在选择某个策略si时的收益，即联保企业在选择清偿贷款和违约逃债时的收益.

2.2.2 收益博弈分析基于上述假设，对博弈模型中的参数进行设定：

1)甲盈利能力强于乙，因此在相同贷款金额的情况下，甲获得M单位银行贷款的收益E甲大于乙的收益E乙，即E甲>E乙；

2)联保贷款的实际贷款执行利率为r，假设商业银行资金为C，为了追求利润最大化，则有MR=MC，即M*r=C.

3)当甲乙都偿还贷款时，甲收益为E甲-M*r，乙收益为E乙-M*r；当甲偿还贷款而乙违约逃债时，甲的收益为E甲-2M*r，乙为E乙；当企业甲违约逃债而乙偿还贷款时，甲的收益为E甲，乙为E乙-2M*r；当甲、乙双方均违约时，即没有任何一方愿意偿还贷款，此时效用最小，为了简化博弈模型，两者收益设定为0. 博弈双方收益矩阵如表1，可以看出，本博弈的纳什均衡解为甲“偿还贷款”和乙“搭便车”.

表1联保企业偿还贷款的博弈模型

甲企业乙企业偿还贷款搭便车偿还贷款E甲-M*r,E乙-M*rE甲-2M*r,E乙搭便车E甲,E乙-2M*r0,0

表2新联保企业偿还贷款的博弈模型

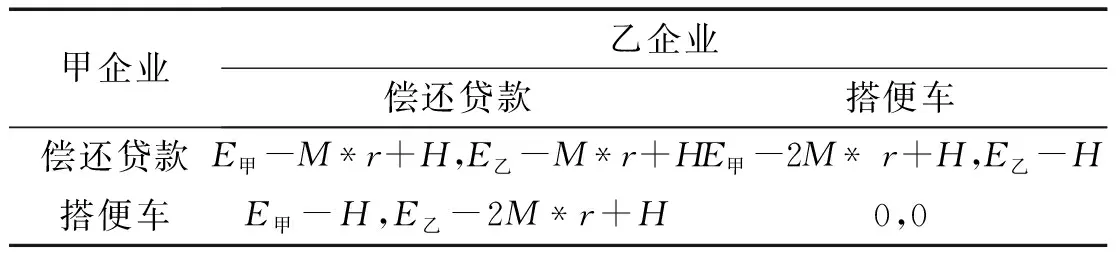
甲企业乙企业偿还贷款搭便车偿还贷款E甲-M*r+H,E乙-M*r+HE甲-2M* r+H,E乙-H搭便车E甲-H,E乙-2M*r+H0,0

3 优化博弈模型

要使“联保机制”有效，联保贷款发挥最大效益，只有甲乙双方都选择偿还才可以实现. 因此，应引入适当的合作机制，差别化对待偿还款企业和违约企业. 本文将“信用等级制度”引入模型，信用等级越高说明信用状况越好，未来可以获得银行融资收益越大. 假设H表示信用收益贴现值，即企业在当前信用等级下，商业银行融资规模带来的未来收益贴现值，用来衡量信用等级上升或者下降未来带来的收益或损失. 在新的业务模式下，对于按期偿还贷款的企业，银行给予提升信用等级的奖励，即在模型收益矩阵中相应的增加收益贴现值(H)，减少偿债企业“偿还贷款”成本；对于违约逃债的企业，银行给予降低其信用等级的惩罚，即在模型收益矩阵中相应地减少收益贴现值(H)，增加逃债企业“搭便车”成本，从而对其再融资进行限制，约束逃债行为.

通过信用等级约束制度的引入，企业“偿还贷款”的收益增加，“违约逃债”的成本也增加，新的博弈模型如表2. 由于信用等级的提升或者降低幅度是有限的，因此本文假设在新的博弈模型下不可能出现(偿还贷款，偿还贷款)策略的纳什均衡.

4 强化学习在博弈中的策略选择

传统博弈论的基本假设为博弈方均为理性的，而在现实中是难以实现的. 因为博弈的一方不仅要保证自身理性而且也要保证对手理智和不冲动，因此各方难以达到完全理性的状态，纳什均衡在这种状况下难以实现，应当充分考虑博弈方非理性的状况，即建立有限理性的博弈分析框架.

对于偿还贷款，参与企业采取的策略，也将对银行授信额度和其他企业的反应等环境因素造成影响. 而环境又会反作用于企业，影响其下一步的策略选择，如此迭代直至产生最优策略，即为马尔科夫决策过程；并且在与环境交互过程中，联保贷款企业具有自主学习能力. 因此，将联保企业偿还贷款的博弈模型置入强化学习框架中，用强化学习算法研究新的联保贷款业务模式下博弈各方偿还贷款的概率.

马尔科夫决策过程是刻画强化学习中环境的标准形式，可以用如下序列表示.

智能体位于状态s0，执行一个动作a0进入s1状态，环境给出了r1的反馈奖励，后由状态s1进入状态s2，环境又给出了r2的反馈奖励，依次迭代直至终止状态. 强化学习算法是研究强化学习的主要算法之一，在实际应用中较为广泛和普遍. 强化学习求解的基本原理[13]是：给定一个有限离散的马尔科夫决策过程MDP={S，A，Pr，P，γ}，其中s∈S表示智能体所处状态，a∈A表示智能体采取的动作，Pr表示状态转移的概率，P表示从当前状态运动到下一状态所获得的奖励，γ表示衰退系数，γ∈[0，1]. 首先生成初始状态s，再寻找到一个最优策略л*，使得其动作价值函数值(强化值)最大，即策略优化过程. 在每个状态采取行动之后，系统将根据选择的最佳л*计算Qл值，即策略评估，求解过程即为策略优化和策略评估的交替迭代中优化参数的过程[14]. 因此，要求得智能体位于状态s时，按照策略л*采取行动a后，在未来所获得反馈值的期望，需要引入动作价值函数的贝尔曼方程：

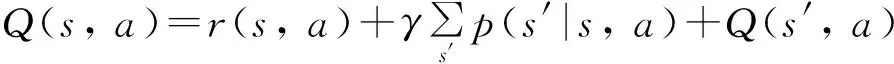
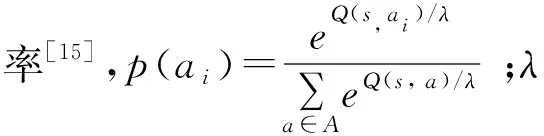
博弈参与方的目标是自身利益最大化，即实现maxaQл(s，a). 在策略优化和评估过程中，基于时序差分的算法被提出，即智能体首先随机初始化Q(s，a)，在时间t时，根据当前Q值进行策略优化，选择某一行动观察执行该行动后的瞬时回报R，再根据Q值迭代关系式进行策略评估和更新Q值，表达式为

Qt+1(s,a)=(1-αt)Qt(s,a)+αt[rt+λmaxQtb(s′,b)]

其中α∈[0，1]，表示学习效率，当αt随着时间减小时，该算法迅速收敛；b表示在新策略下执行下一个动作.

5 仿真实验

本文以建立强化学习优化模型作为分析框架，利用算例说明企业在联保贷款业务模式优化博弈中偿还贷款行为的出现频率，对比分析新的机制对于企业选择偿还贷款次数选择的影响，新旧博弈模型的支付矩阵分别如表3、4所示. 在新模型中，引入信用收益贴现值，当企业选择偿还贷款时，给予新增3个单位的收益奖励；当选择违约逃债时，给予减少3个单位收益的惩罚.

表3 旧博弈模型的支付矩阵

表4进化博弈模型的支付矩阵

甲企业乙企业偿还贷款搭便车偿还贷款11,99,5搭便车7,70,0

可以看出，任何理性博弈方都会选择“搭便车”的占优策略. 然而，为了实现收益最大化，博弈方将会选择偿还贷款. 于是，将强化学习算法置于博弈模型中，智能体设定为甲、乙两个企业，状态设定为甲乙双方行动组合，智能体通过与环境的交互学习，寻找到优化模型中的最优策略. 博弈方执行某个行动之后的即时回报可以由支付矩阵得到，最后博弈方的累计博弈总期望可以用与当前状态和行动都相关的动作价值函数表示，动作价值函数通过强化值进行储存. 因此，强化值代表博弈方在当前状态下选择最优策略采取行动后最大化收益期望. 基于强化学习的两个智能体进化博弈模型的迭代策略算法如下：

步骤1 令t=0，Q=0，智能体(博弈双方)随机产生前两步行动；

步骤2 通过前两次策略的选择，确定博弈方的状态S，用概率函数(2)计算选择下一步行动的概率，并进行比较确定下一步的行动；

步骤3 利用动作价值函数迭代表达式(4)对Q值进行更新；

步骤4 转入步骤2，令t=t+1，继续迭代，直到收敛为止.

经过40步的迭代，Q值误差趋于收敛，停止迭代，得到Q值迭代曲线如图1所示.

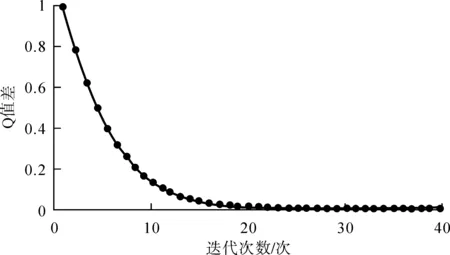
图1 强化学习博弈模型中强化值迭代图

本文设定博弈模型中γ=0.8，重复300博弈次数. 结果显示，对于旧博弈模型来说，甲乙双方选择“偿还贷款”次数为99次；而在新博弈模型中，双方选择“偿还贷款”次数高达242次，直至最终策略稳定于“偿还贷款”，没有任何博弈方选择“搭便车”. 表明进化后的博弈模型让联保贷款参与企业更愿意选择偿还贷款，联保贷款业务模式更优化、有效. 也就是说，“信用等级制度”的引入，使得企业“搭便车”违约逃债的成本更高，一次违约逃债将会影响其在银行系统的信用等级. 信用等级降低，违约企业很可能面临无法再融资的局面. 企业在不断的试错和环境交互中，逐步放弃“搭便车”而选择“偿还贷款”这一策略；另一方面，按时还款还可以偿债企业提升其信用等级，增加其在银行的融资规模，提升了融资收益，也将进一步激发“偿还贷款”的意愿. 因此，优化后的联保贷款业务模式可以有效地实现偿还贷款的帕累托最优均衡.

6 结语

随着“人工智能+”模式的发展，人工智能被应用到了各领域，然而“人工智能+金融”模式的研究尚未充分开发. 同时，联保贷款作为我国中小企业融资的有效助力手段得到了商业银行、中小企业以及国家的高度重视，但是其中存在的问题仍未得到有效解决. 本文利用人工智能中的强化学习算法解决联保贷款中存在的“搭便车”问题；针对联保贷款参与各方具备强化学习的能力，提出基于强化学习的演化博弈理论优化了模型，并引入“信用等级制度”来约束联保贷款参与各方的还款行为. 算例结果发现，优化后的业务模式有效地降低了博弈各方选择违约逃债的概率，提高了联保贷款参与各方到期偿还贷款的概率.

本文对于联保贷款参与企业的自主学习过程是利用转移概率确定的策略调整，并未完全考虑联保贷款参与各方的相互作用以及与环境交互的影响. 因此，利用复杂网络进化博弈研究参保企业之间的策略选择过程是未来重要的研究方向.