BIM 技术推广中利益相关主体演化博弈研究

胡继文

（江西理工大学经济管理学院，江西 赣州 341000）

0 引言

随着中国经济的飞速发展， 中国城市化进程也逐步加快， 建筑业已成为我国国民经济的重要支柱产业之一。 但建筑业的经济效益一直提升不快。 BIM 技术的应用能有效避免建设过程中的“错、漏、碰、缺”[1]等问题，从而极大地提高工程项目效益。

1 构建演化博弈模型

1.1 模型假设

选取政府和建设单位作为博弈的主体， 且政府和建设单位都是有限理性的， 政府是从长期社会效益和可持续发展的角度来决定是否采用激励政策，而建设单位的目的是实现利益最大化。 建设单位和政府在有限理性的前提下会根据对方的策略进行多次博弈，以此来寻找最优的策略。

假设1：在有限理性的前提下，政府选择的策略为A1={不激励， 激励}， 建设单位选择的策略为A2={采用BIM 技术，不采用BIM 技术}。 假设政府采取激励的概率为x， 则采取不激励的概率为1-x；建设单位采取在建筑中采用BIM 技术的概率为y，则不采用BIM 技术的概率为1-y。

假设2：a1表示政府维持现状， 不采取激励措施的收益；a2表示政府不采取激励政策下建设单位主动采用BIM 技术时的收益；a3表示激励政策推行成功时在建设项目中获得的额外收益，如资源节约、 建设效率加快和公信力提高；a4表示政府推行激励政策所付出的成本；αa5表示在激励政策下建设单位采用BIM 技术时政府给其的补贴， 其中α表示补贴系数；b1表示建设单位采用BIM 技术时的收益；b2表示建设单位不采用BIM 技术时的收益；b3表示建设单位采用BIM 技术时所付出的增量成本；βb4表示政府对建设单位不采用BIM 技术时的罚金，其中β 表示收取的罚金系数。

根据上述假设条件，政府和建设单位演化博弈模型的支付矩阵见表1。

1.2 模型建立

（1）政府复制动态方程

根据支付矩阵可知，政府选择激励时的期望收益如式（1）所示。

政府选择不激励时的期望收益如式（2）所示。

表1 政府与建设单位的博奕支付矩阵

政府选择激励和不激励时的平均期望收益如式（3）所示。收益是相同的，无论x 取何值，政府都是稳定状态。

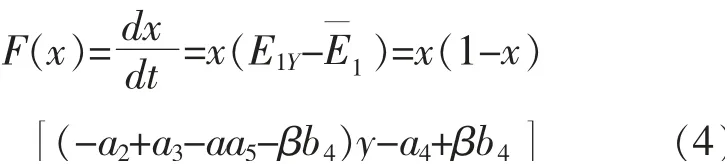
由式（1）～（3）可知，政府的复制动态方程如式（4）所示。则x=1 是唯一的演化稳定策略。即建设单位以高于（-a4+βb4）/（a2-a3+αa5+βb4） 的概率采用BIM 技术时，政府将由“不激励”向“激励”政策转移。

对F（x）进行求导可得式（5）。

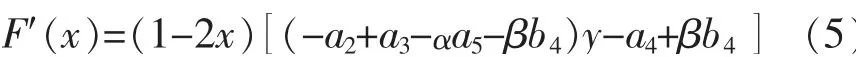
（2）建设单位复制动态方程

建设单位选择采用BIM 技术时的期望收益如式（6）所示。则x=0 是唯一的演化稳定策略。即建设单位以低于（-a4+βb4）/（a2-a3+αa5+βb4） 的概率采用BIM 技术时，政府将由“激励”向“不激励”政策转移。

1.3.2 建设单位单方策略稳定性分析

同理， 当F （y）=0 时， 解 得：y=0，y=1，x*=

建设单位选择不采用BIM 技术时的期望收益为如式（7）所示。

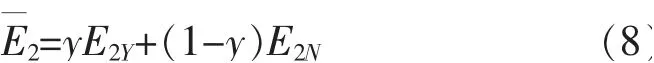
建设单位选择采用和不采用BIM 技术时的平均期望收益如式（8）所示。即政府以（-b1+b2+b3）/（αa5+βb4）的概率采取激励政策时，建设单位采取“采用BIM 技术”或“不采用BIM 技术”策略时收益是相同的，无论y 取何值，建设单位都是稳定状态。

由式（5）～（7）可知，建设单位的复制动态方程如式（9）所示。

对F(y)进行求导可得式（10）。

1.3 演化博弈稳定性分析

1.3.1 政府单方策略稳定性分析

根据复制动态方程定理可知， 当F （x）=0，F′（x）＜0 时，该x 为演化稳定策略。 当F（x）=0 时，解得

1.3.3 混合策略稳定性分析

根据Friedman 的研究结论可知，演化博弈系统均衡点的稳定性由雅克比矩阵的局部稳定性分析得到[2]。 对式（4）和（9）求其偏导，可求得雅克比矩阵J,并同时求出雅克比矩阵的行列式DetJ 和迹TrJ。0，即建设单位以（-a4+βb4）/（a2-a3+αa5+βb4）的概率采用BIM 技术时，政府采取“激励”或“不激励”策略时

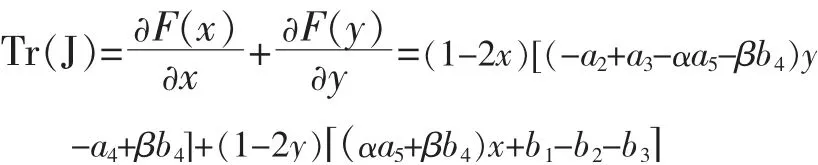
令 （F （x）,F （y））=（0，0）， 得到5 个均衡点（0，0）、（0，1）、（1，0）、（1，1）、（x，y），其中x=（-b1+b2+b3）/（αa5+βb4），y=（-a4+βb4）/（a2-a3+αa5+βb4）。 该系统雅克比矩阵分析见表2。

表2 雅克比矩阵分析

根据常微分方程稳定性分析方法[3]，若某均衡点的Jacobin 矩阵行列式detJ＞0 且迹trJ＜0,则该点就是系统在演化过程中的局部稳定点，即ESS 点。从该系统的雅克比矩阵可以看出， 该系统由-a4+βb4、b1-b2-b3、-a2+a3-a4-αa5和αa5+βb4+b1-b2-b3这4 个变量决定，现对该4 个变量分情况讨论。

（1） 当-a4+βb4＜0，b1-b2-b3＜0 时，即政府对建设单位不采用BIM 技术的惩罚小于激励成本， 建设单位采用BIM 技术的收益小于其采用所增加的成本，若-a2+a3-a4-αa5＞0，αa5+βb4+b1-b2-b3＞0 时，对其系统的均衡点稳定性分析见表3。表3 表明，当-a2+a3-a4-αa5＞0，αa5+βb4+b1-b2-b3＞0 时，系统将出现2 个演化稳定 策 略（0，0）和（1，1），2 个 不 稳 定 策 略（0，1）和（1，0）以及一个鞍点（x*，y*），该系统的动态演化相位图见图1。

表3 系统均衡点稳定性分析

由图1 可知：当政府和建设单位选择的初始策略位于区域①④内部时， 双方的演化博弈将向（0，0）演化，即（不激励,不采用）将是政府和建设单位的必然选择；当政府和建设单位选择的初始策略位于区域②③内部时， 双方的演化博弈将向（1，1）演化，即政府选择激励策略，建设单位也选择采用BIM 技术。显然，最满意的策略是使系统向（1，1）演化，若想使系统的演化最终稳定于（激励,采用）的概率增大，可以通过改变参数的大小使得x* 和y*的值降低。 根据x*=（-b1+b2+b3）/（aa5+βb4），y*=（-a4+βb4）/（a2-a3+aa5+βb4）可知，当政府和建设单位的增量收益增加或者政府提高对建设单位不采用BIM 技术时的税收，双方的演化博弈将会向（1，1）演化，即出现政府采取激励政策， 建设单位采取采用BIM 技术的理想策略。

（2）当-a4+βb4＜0，b1-b2-b3＜0 时，-a2+a3-a4-αa5和αa5+βb4+b1-b2-b3进行变化时，对其系统的均衡点稳定性分析见表4。 由表4 可知，当政府对建设单位不采用BIM技术的惩罚小于其激励成本， 建设单位采用BIM技术的收益小于其采用所增加的成本时，若政府和建设单位中任意一方的利益小于0 时，双方的博弈都会向（0，0）方向演化，即出现政府选择不激励，建设单位也选择不采用的最不理想状态。

表4 -a5+βb4＜0，b1-b2-b3＜0 时其他参数变化稳定性分析

（3）当-a4+βb4＞0，b1-b2-b3＜0 时，-a2+a3-a4-αa5和αa5+βb4+b1-b2-b3进行变化时， 对其系统的均衡点稳定性分析见表5。当政府对建设单位不采用BIM技术的惩罚大于其激励成本， 建设单位采用BIM技术的收益小于其采用所增加的成本时，若政府和建设单位能同时收益时，系统将会向（激励,采用）演化；若政府采取激励措施时的激励成本和补贴大于其获得的额外收益， 建设单位净收益大于0 时，系统没有稳定状态； 若建设单位的净收益小于0时，建设单位将会趋向于选择不采用BIM 技术，因政府对建设单位不采用BIM 技术的惩罚大于其激励成本，此时政府会选择激励策略，系统将会向（激励,不采用）演化。

表5 -a5+βb4＞0，b1-b2-b3＜0 时其他参数变化稳定性分析

（4）当b1-b2-b3＞0 时，αa5+βb4+b1-b2-b3恒大于0，系统只有4 个均衡点（0，0）、（0，1）、（1，0）和（1，1）。 -a4+βb4和-a2+a3-a4-αa5进行变化时， 对其系统的均衡点稳定性分析见表6。 由于αa5+βb4+b1-b2-b3恒大于0，即建设单位选择采用BIM 技术的净收益恒大于0，建设单位会选择积极采用的策略。当政府采取激励措施时的激励成本和补贴小于其获得的额外收益时，政府将会积极采取激励措施，系统将会向（激励,采用）方向演化；当政府采取激励措施时的总收益小于0 时，政府将采取不监管的政策，系统将会向（不激励，不采用）方向演化。

表6 b1-b2-b3＞0 时其他参数变化稳定性分析

2 仿真

2.1 系统动力学模型的建立

为进一步分析变量的取值变化对政府和建设单位在BIM 技术发展博弈中的策略选择， 采用系统动力学仿真软件Vensim 对上述博弈进行仿真分析，该系统动力学模型见图2。

图2 演化博弈系统动力学模型

2.2 模型仿真分析

初始值的选定主要考虑各个变量的改变对政府、建设单位策略选择的影响，每个变量的取值不代表真实工程中政府和建设单位的损益值。现对模型进行赋值，模型初始值假设为：a1=0.3，a2=0.3，a3=2，a4=0.5，a5=1，b1=1，b2=0.8，b3=0.5,b4=1，α=0.4，β=0.3。 仿真结果如图3 所示。

从图3 可以看出，政府的激励概率开始有增长的趋势， 但随着建设单位采用BIM 技术意愿的逐渐降低，政府的激励概率也逐渐下降，最终均趋于0。 其主要原因是建设单位采用BIM 技术所需的前期成本过大，其所付出的成本大于在项目中所获得的收益，因此建设单位参与的意愿很低。

图3 初始值时模型仿真结果

为了探讨不同因素对政府和建设单位协同作用产生的影响，对政府、建设单位采用策略下的补贴系数，建设单位采用时的收益b1、成本b3，政府对建设单位不采用时的罚金b4进行敏感性分析，为提高BIM 技术的应用提供建议及参考。

（1）补贴系数α 敏感性分析

改变变量补贴系数的取值，其他变量取值同图3，α 的取值分别为30%，40%,50%， 仿真结果如图4 所示。 当政府对建设单位给予的补贴过低时，相当于建设单位在采用BIM 技术的过程中增加了成本投入，此时无法调动建设单位的积极性，建设单位更加倾向于不采用BIM 技术。 随着补贴系数值的逐渐增大， 建设单位采用BIM 技术的意愿逐渐增强，当政府的补贴力度达到50%时， 政府选择激励的概率也将逐渐趋近于1，系统结果将会趋向于“激励，采用”。 但政府的补贴额度应控制在一定范围内，否则将加重政府的财政压力，不利于BIM 技术的推广。因此，政府可以适当提高补贴力度，有助于双方达到合作共赢的状态。

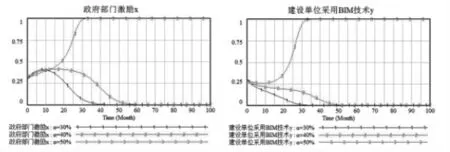
图4 补贴变化时仿真结果

（2）收益b1敏感性分析

改变收益b1的取值， 其他变量取值同图3，b1的取值分别为0.9,1,1.1，仿真结果如图5 所示。 当建设单位采用BIM 技术时获得的收益较低时，建设单位越趋向于不采用BIM 技术， 此时政府通过加大对BIM 技术的激励和推广使得BIM 技术的长期效益得到提高， 建设单位采用BIM 技术的意愿将会迅速上升，当收益b1增至1.1 时，建设单位应用BIM 技术在项目中获得的收益大于其成本，此时建设单位会选择采用。 因此，增大建设单位采用时的收益是能促进政府和建设单位协同合作的有效方式。

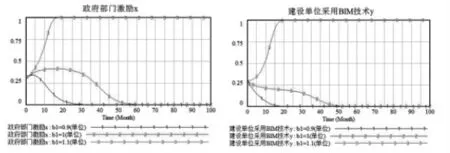
图5 收益变化时仿真结果

（3）成本b3敏感性分析

改变成本b3的取值， 其他变量取值同图3，b3的取值分别为0.6,0.5,0.4，仿真结果如图6 所示。当建设单位采用BIM 的成本逐渐减小时， 建设单位采用BIM 技术的概率相应地逐渐增大， 直至趋向于1。 其原因是降低成本能够减轻建设单位的生产成本，提高采用BIM 技术时的增量经济收益，以此提高建设单位采用的积极性，因政府的策略选择会随着建设单位的策略而变化，政府也会更倾向于采取激励措施，即降低成本能有效地使系统结果趋向于（激励，采用）。

图6 成本变化时仿真结果

（4）罚金系数β 敏感性分析

改变罚金系数β 的取值， 其他变量取值同图3，β 的取值分别为20%,30%,40%，仿真结果如图7所示。 仿真结果表明，当政府对建设单位收取的罚金从20%增加至40%时， 建设单位意识到采用BIM 技术才能获得更大的经济利益，故建设单位使用BIM 技术的意愿将会增强。 因此，政府可以通过各种手段获取建设单位在工程中采用BIM 的程度， 针对不同情况增加罚金额度才能使（激励，采用）成为稳定均衡策略。

图7 税收变化时仿真结果

3 BIM 技术发展的对策建议

在BIM 技术的应用过程中， 政府和建设单位都会互相受到对方决策的影响，双方最终的稳定策略也受到政府补贴力度、 建设单位应用BIM 的额外成本、政府对建设单位的惩罚力度等多种因素影响。 因此，为加强企业对BIM 技术的应用提出以下建议：

（1）加大政策激励力度

政府应采取奖励的方式来推进建设单位对BIM 技术的应用， 即对应用BIM 技术的企业提供一定程度上的补贴， 同时根据企业应用BIM 技术的情况给与税收优惠， 以此来改善BIM 应用的现状。

（2）完善国内相关法规

政府应完善国内与BIM 相关的法律法规，加大对建设单位的惩罚力度， 规范建设单位对BIM技术的使用。但是过大的惩罚也会影响建设单位采用BIM 的稳定性。 因此政府应结合奖励方式多角度控制，制定一个稳定完善的奖惩机制。

（3）提高对BIM 技术的认识

我国对BIM 技术的应用仍处于初级阶段，因此政府应加强对BIM 的宣传和培训。 应积极培训BIM 技术人员， 开发适合我国行业现状的软件，降低企业使用BIM 技术的额外成本。 同时，大力宣传采用BIM 所获得的长期效益， 增强企业使用BIM技术的主动性。