基于一类广义三阶KdV方程的精确解探讨
李奇芳
(山西财贸职业技术学院 山西 太原 030031)
1 研究背景
在自然科学和工程技术里,不少现象不能采用线性模型描述,如大幅度摆动,自激震荡,电路的机理等.所以,近年来,对非线性问题的研究在物理,化学,生物,数学等领域得到了广泛而深入的开展,特别是寻找非线性方程的精确解受到广泛关注.由于非线性现象与非线性偏微分方程有着密切的联系,非线性偏微分方程的精确解在许多的科技领域发挥着重要作用,因此,为了更好的理解自然界中众多的非线性现象的机制,必须知道与这些非线性现象相符的非线性偏微分方程的精确解。郭婷婷等人(2017)提出运用双Bell多项式确定KdV方程的双线性,并求得其递推公式[1]。郭峰等人(2018)提出利用平均值离散梯度的模式验证KdV方程组能量守恒理论的正确性[2]。赵露等人(2018)通过简化的双典型方法测试双模KdV方程中的线性及非线性参数,从而得到精确解[3]。基于此,可以看出,利用KdV方程算法求解非线性模型,并用这种方法求解CH-DP方程更加简洁明了。
2 KdV方程的概述
2.1 研究方向

2.2 研究方法
对于一个关于独立变量的一类非线性偏微分方程如(1)所示:
H1(u,ux,ut,uxx,uxt,utt,…)=0.
(1)
该方法通过下面四个步骤寻找非线性偏微分方程的精确解,如方程(2)所示:
u(x,t)=φ(x,t)+R,
(2)
其中R任意常数,将变换(1)代入(2)中,则公式1转换为下面的形式,如方程(3)所示:
H2(φ,φx,φt,φtt,φxt,φtt…)=0.
(3)
而后确定常数R的值.如方程(4)所示:
Φ=φ-α2φxx
(4)
其中α≠0,将方程(3)代入方程(4)使方程(4)的各项表达式都包含Φ或者Φ的各阶导数,根据方程各项之间系数的关系,得出R的取值。
(三)例题模拟
例如:考虑如下DGH方程,如方程(5)所示:
ut+2kux+3uux-(uxxt+uuxx+2uxuxx+γuxx=0,
(5)
其中k,γ是任意常数.将公式(2)代入方程(5),如方程(6)所示:
φt+(2k+3R)φx+3φφx-φxx-φφxxx-2φxφxx+(γ-R)φxxx=0.
(6)
方程(6)可变为如方程(7)所示:
(φ-φxx)t+2φx(φ-φxx)+φ(φ-φxx)x=-(2k+3R)φx-(γ-R)φxxx·
(7)
由方程(4),取α2=1得如方程(8)所示:
Φt+2φxΦ+φΦx=-(2k+3R)φx-(γ-R)φxxx·
(8)
为了使方程(8)的每一项都包含Φ或者Φ的各阶导数,如方程(9)所示:
-(2k+3R)=γ-R,
(9)
化简可得如方程(10)所示:
(10)
将方程(10)代入方程(8)得如方程(11)所示:
(11)
显然,Φ=0是方程(11)的解.
求方程Φ=0的解.注意到Φ=φ-α2φxx=0是线性微分方程,因此容易得到该方程的更一般形式的解.获得方程(1)的精确解。通过方程(4)的变形,方程(11)的每一项都包含Φ或者Φ的各阶导数,则当φ(x,t)是方程Φ=0的解时,φ(x,t)也是方程(3)的解.实际上,在方程(11)中,当φ(x,t)是方程Φ=0的解时,φ(x,t)也是方程(11)的解.通过改变常数t的取值来扩展方程Φ=0的基础解,从而得到方程(1)的一系列的精确解.
3 一类广义三阶KdV方程的求解
3.1 一类广义三阶KdV方程的精确解
在这部分,将应用这种简单的方法得到广义三阶KdV方程的不同解.广义三阶KdV方程如方程(12)所示:
(12)
其中α,β,ν为任意常数.
令u(x,t)=φ(x,t)+R,将其代入方程(12)后如方程(13)所示:
(13)
根据研究方法,方程(13)可转换如方程(14)所示:
(14)
令Φ=φ+νφxx,为了使方程(14)的每一项包含Φ或者Φ的各阶导数,如方程(15)所示:
(15)
化简可得如方程(16)所示:
(16)
因此方程(14)可以写为如方程(17)所示:
(17)
注意到Φ=φ+νφxx,所以,方程(17)可以变为如方程(18)所示:
(18)
3.2 情景分析
我们需考虑方程(19)的解:
φ+νφxx=0.
(19)
情形假设φ<0.
容易求出方程(19)的基本解组如方程(20)所示:
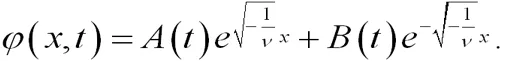
(20)
其中A(t),B(t)是任意可微函数. 是方程(19)的解,易知如方程(21)、公式(22)所示:
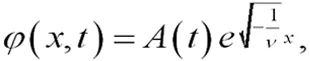
(21)
和
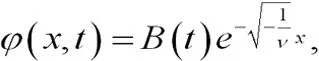
(22)
由方程(23)、方程(24)所示:

(23)
和

(24)
可得如方程(25)、方程(26)也是方程(19)的解:
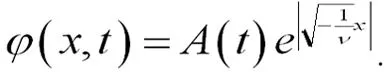
(25)
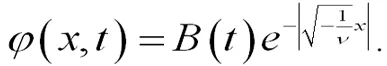
(26)
所以,当如方程(27)所示时,也是方程(19)的解.
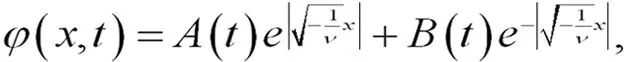
(27)
由于A(t),B(t)是任意可微函数,则可以扩展解方程(21)后,如方程(28)所示:
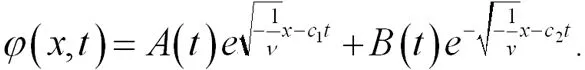
(28)
其中c1,c2为任意常数.
不妨假设0 (29) 所以可得如方程(30)所示也是方程(19)的解. (30) 此外,还能扩展方程(21)如方程(31)所示: (31) 其p(t),q(t)中为任意函数,通过检验,也是方程(19)的解. 类似地,对任意的x构造,如方程(32)所示: (32) 所以方程(32)也是方程(19)的解. (32) (33) (34) 也是方程(19)的解.其中Ai(t),Bj(t),pi(t),qj(t)是任意可微函数,i=1,2,…N,j=1,2,…M,N,M是任意正整数。类似可得如方程(35)、方程(36)也是方程(19)的解[5]. (35) (36) 根据双曲函数的定义,可知方程(37)、方程(38)也是方程(19)的解. (37) (38) 情形ν>0. 容易求出方程(19)的基本解组为如方程(39)、方程(40)所示: (39) 其中c(t)为任意可微函数[6]。 (40) 值得注意的是,从上面的这些构造过程中,可以得到方程(19)的其他精确解,由于篇幅所限,在这里给予省略. 故方程(13)有下列解,如方程(41)-方程(50)所示: (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) 根据所求的精确解,利用Maple软件将方程(41)-(45)及(50)的解的波形图绘制如下: 绘图时,方程(41)、方程(42)、方程(44)都取ν=-1,α=-1,β=1,N=1,M=1,方程(50)取ν=3,α=1,β=3,N=1,M=1.如图1-4所示: 图1(a)是当A(t)=log10t,B(t)=sint,x[-20,20],t[1,10]时,方程(41)的波形图. (b)是当A(t)=sin,B(t)=cost,x[-30,30],t[-15,15]时,方程(41)的波形图. (c)是当A(t)=sinht,B(t)=tant,p(t)=sint,q(t)=sint,x[-40,40],t[-1,1]时,方程(42)的波形图. (d)是当A(t)=sinht,B(t)=cost,p(t)=sint2,q(t)=sint3,x[-2,2],t[-8,8]时,方程(42)的波形图. (e)是当A(t)=t2,B(t)=t,p(t)=sint2,q(t)=cost3,x[-3,3],t[-4,4]时,方程(44)的波形图. (d)是当A(t)=et2,B(t)=cost,p(t)=sint2,q(t)=cost3,x[-10,40],t[-1,1]时,方程(44)的波形图. (g)是当C(t)=log10t,x[-20,20],t[0.1,10]时,方程(50)的波形图. (h)是当C(t)=sin10t,x[3.5,11],t[-13,13]时,方程(50)的波形图. 求解非线性偏微分方程的精确解是一种简单方法,这种方法对于求解非线性偏微分方程是有效和直接的,它可以避免乏味的重复计算。这种方法之所以简单关键在将原方程进行转化,转化为多个简单的常系数高阶常微分方程,最终只需求出简单的常系数高阶常微分方程的解。便可得出原方程的解。本文以广义三阶KdV方程为例,用简单方法求出了它的许多精确解,并且借助数学软件MAPLE,在一定参数条件下得到了该方程的一些特殊解的波形图。



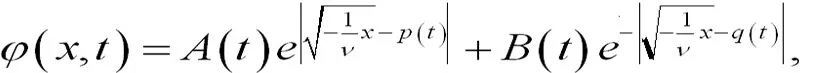
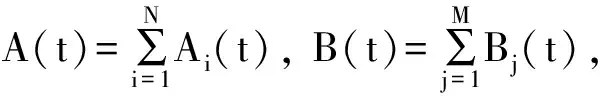
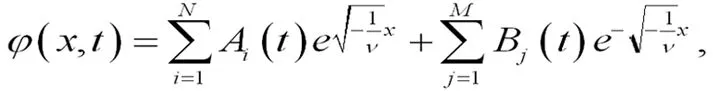






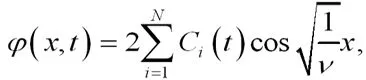



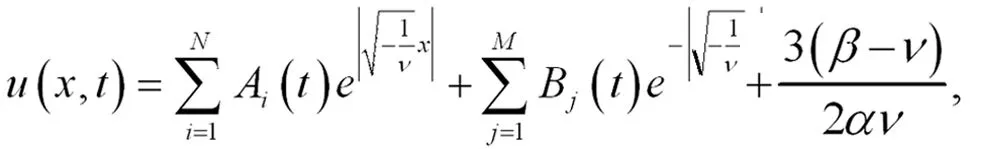
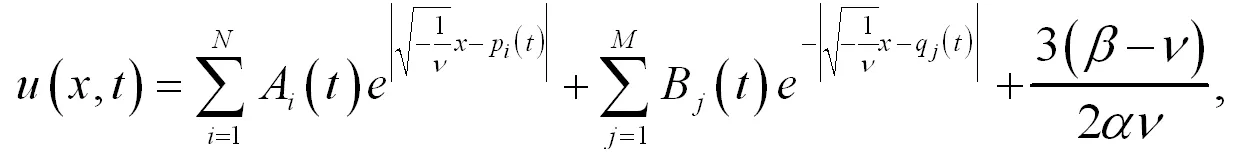




(三)精确解的波形图


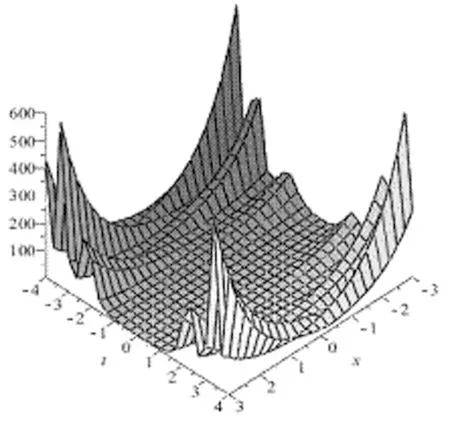

四、结论

