高速枕式包装机横封机构可靠性分析

于道航， 严国平， 钟 飞， 杨小俊， 万乾程

(湖北工业大学机械工程学院， 湖北 武汉 430068)

蒙特卡罗可靠性分析方法通过大量随机模拟对研究对象进行可靠性分析，如果选择的随机数数量过少，结果就会产生严重偏差，国内外一些研究者对此进行了大量的研究。理论上，吕震宙[1-3]详细介绍了蒙特卡罗可靠性及可靠性灵敏度分析理论，并阐述了相关推导过程及计算方法；在工程应用领域，龙东平[4]等人依据蒙特卡罗可靠度性方法，对机械零件的应力与强度的关系进行模拟，并得出机械零件的可靠性指标；刘瑞，宿吉鹏[5-6]以机械手为研究对象，讨论了铰间隙位移、速度及加速度的可靠性分析。AIAA[7]将蒙特卡罗可靠性分析法应用于风力电机的可靠性分析，Zhang[8]提出QMC法以降低样本数并提高计算精度。上述研究很少涉及包装领域。由于包装机械的灵巧性及精密性，其设计运行的可靠性要求更为突出，故本文将以枕型袋包装机横封机构作为研究对象，基于蒙特卡罗可靠性分析法，对横封机构在不同公差等级下的运动精度可靠性进行计算分析，力求为尺寸公差等级选取的合理性提供理论依据。

1 横封机构运动原理

枕型袋包装机横封机构[9]的工作结构如图1所示。

根据机构的运动原理，可将该机构中横封头、曲柄以及连杆构成的一组曲柄滑块机构作为研究对象，其运动简图如图2所示。

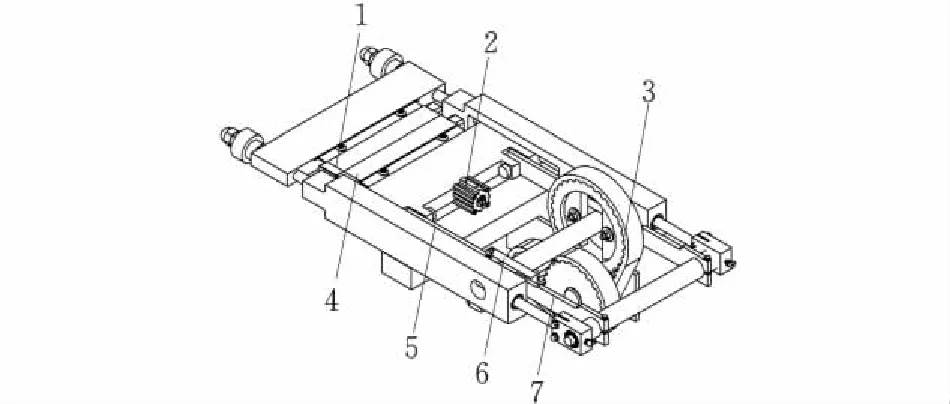
1-横封头a；2-气缸；3-带轮；4-横封头b； 5-连杆b；6-曲柄；7-连杆a图 1 横封机构结构图

图 2 机构运动简图

OB、BC分别为曲柄和连杆，滑块C代表横封头，D为包装袋，横封头与包装袋之间的距离为CD=x，当x=0时为热封的理想位置，x′ 代表运动误差。

2 可靠性及可靠性灵敏度计算

如图2所示，根据几何关系，机构运动方程：

(1)

式中：x为滑块运动距离，r为曲柄长度，l为连杆长度，φ为曲柄角位移。

由于OB及BC在长度上会有偏差，可表达为r1，l1。以位置误差x′作为机构运动的位置有效域，根据式(1)构建功能函数：

(2)

设r，l满足高斯分布。根据均值μ、标准差σ得到联合概率密度函数：

(3)

式中：μr，μl为曲柄连杆的均值；σr，σl曲柄连杆长度分布方差。

依据蒙特卡罗可靠性分析理论，由联合概率密度函数随机产生N个基本变量，并将这N个随机变量代入功能函数，统计最终落入失效域的基本变量的个数Nf,最终可求得失效概率估计值[1]

Pf=Nf/N

(4)

失效概率估计值的方差

(5)

失效概率估计值的变异系数

(6)

可靠性灵敏度可以描述基本变量分布参数对失效概率的影响程度[1]，在数学表达式上可表述为失效概率Pf对基本变量分布参数θx的偏导数。本文以μr、μl、σr、σl四个基本变量作为可靠性计算的分布参数，根据下式进行可靠性灵敏度相关计算：

(7)

式中：xj是按照联合概率密度函数抽取的N个样本中的第j个样本。 可靠性灵敏度估计值的方差表达式为：

(8)

其估计值的变异系数表达式为：

(9)

3 具体算例

以某枕型袋包装机横封机构为例，相应参数为曲柄OB=45 mm，连杆BC=200 mm，均值μr= 45 mm，μl= 200 mm。以IT9为例，依据3σ准则得标准差σr=0.062/3，σl=0.115/3,0

图 3 曲柄长度取样分布

由图3可知，在样本数为106前提下，曲柄长度的采样结果符合前述只允许负公差存在的工况要求，为后续相关研究计算工作的准确性奠定了基础。连杆采样情况与曲柄采样类似。

3.1 位置可靠性结果分析

依据式(2)-(4)进行位置可靠性计算，为保证概率计算结果数据的可靠性，分别以样本数为107和108两个数量级进行计算与比较，将φ=0时得到的蒙特卡罗可靠性计算结果列于表1，并选取满足热封工作要求的尺寸精度。

表1 φ=0时失效概率P

根据表1的计算结果，以95%的可靠度为设计目标，则可选取公差等级为IT9的曲柄与连杆，从而满足该机构在热封工作时的设计需求。另外，表1表明，在两个足够大的样本数数量级下，蒙特卡罗可靠性计算的失效概率几乎相同，这说明采用本文所述方法对横封机构进行可靠性计算的结果具有良好的可信度，计算消除了样本数过少造成的偶然因素的影响。

前文对φ=0时工作位置的情况进行了分析，但同样可以采用其他角度作为工作位置的工况。为了探讨何种角度作为工作位置较为合理，以IT9为例，绘制角位移与失效概率的对应关系(图4)。

图 4 曲柄转角-失效概率

如图4可知，随着曲柄角位移φ的增加，机构的失效率呈非线性减小趋势，在0～60°间失效概率波动较大，但随着曲柄角位移的增大，失效概率波动减小，说明曲柄角位移φ在开始角度时波动较大，后续波动较小，但整体来看，机构位置的失效概率显著降低。因此，仅从工作角度来看，当曲柄转角在0°～100°之间，其工作位置所在角度越大，失效率则越低。

3.2 可靠性灵敏度结果分析

根据式(5)-(9)对φ= 0°时的可靠性灵敏度数据进行相关计算。计算结果列于表2。

由表2可知，随着精度等级的提高，曲柄与连杆的失效概率降低且离散程度降低，另外，μr、μl、σr、σl对失效概率的影响整体上呈现降低的趋势。这表明，随着精度等级的提高，该机构可靠性、稳定性趋好。

4 结束语

1)通过对枕型袋包装机横封机构的运动位置精度需求分析，计算出了蒙特卡罗可靠性数据及可靠性灵敏度数据，从所得数据分析得出IT9及更高公差等级满足位置精度需求且可靠性高于95%。但公差等级的提升，也伴随着加工成本的极大提高，因此，IT9为更合理的选择。

2)当角位移0～60°时，失效概率波动较大，可考虑将热封工位对应的曲柄角位移增大，避免不同曲柄角位移的失效概率相差过大，以提高机构稳定性。

3)以本文所用方法进行相关零件设计时的公差等级选择，可得到更为直观的数据，进而提高设计的可靠性。