三角形“边分比”性质的应用举例及其推广

广东省广州市铁一中学 (510600) 何重飞华南师范大学数学科学学院 (510631) 吴 康

丰富繁杂的平面几何世界，有一些命题或者结论及其模型简洁明了，但在解题应用当中却是一把利器，正所谓“小结论，大应用”.下面笔者介绍一个涉及三角形边角关系的“边分比”性质，并对性质的简单应用及其推广加以举例探究.

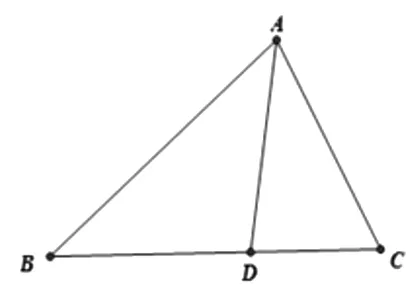
图1

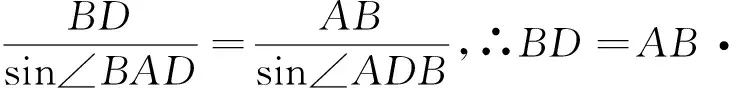
利用上述“边分比”性质或其推论可以证明平面几何中的多个经典定理.

图2

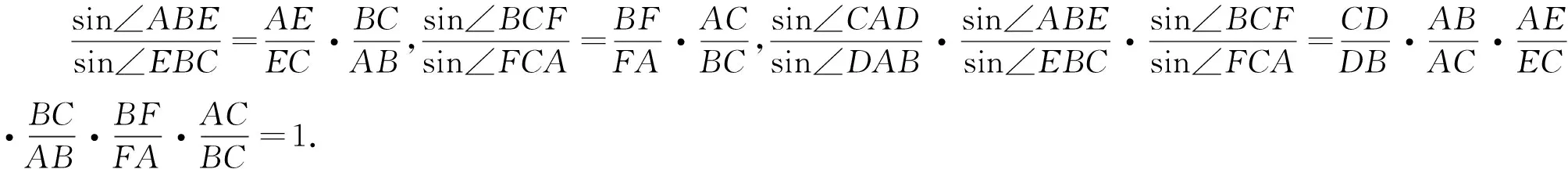
图3

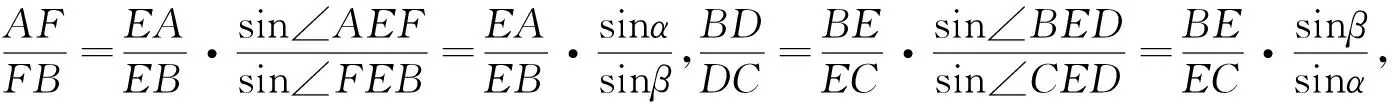
例4 (莱莫恩定理)过ΔABC的三个顶点A,B,C作它的外接圆的切线，分别和BC,CA,BA的延长线交于P,Q,R，则P,Q,R三点共线.

图4

图5

例5 (西姆松定理)三角形外接圆上任意一点在三边(或所在直线)上的射影共线.

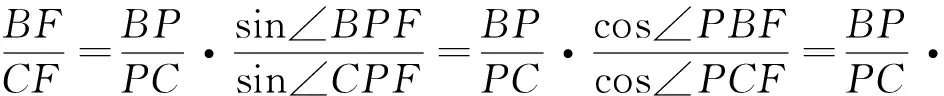
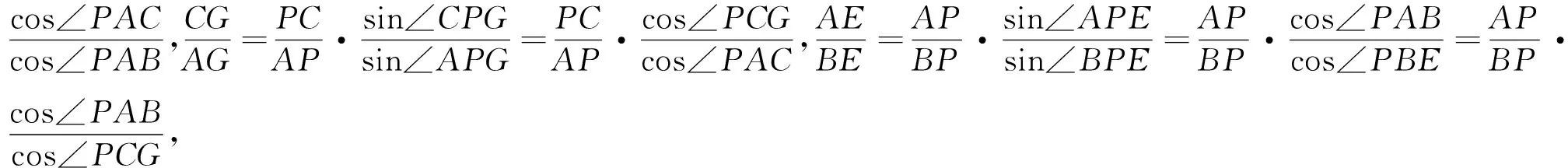
例6 (笛沙格定理)若两个三角形的对应顶点连线交于一点，则对应边所在直线的交点必共线.

图6

利用“边分比”性质或其推论也可以推广平面几何中的经典定理.

例7 (塞瓦定理在平面偶数边形中的推广)在平面2n(n≥2)边形A1A2…A2n中，已知B1,B2,…,B2n分别是线段A1A2,A2A3,…,A2nA1上的点，且A1An+1,A2An+2,…,AnA2n,B1Bn+1,B2Bn+2,…,BnB2n交于点O，则有：

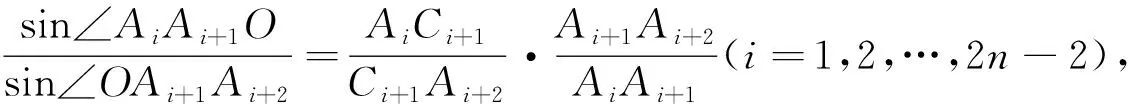
(塞瓦定理在平面奇数边形的推广)在平面2n-1(n≥2)边形A1A2…A2n-1中，已知B1,B2,…,B2n-1分别是线段A1A2,A2A3,…,A2n-1A1上的点，且A1Bn,A2Bn+1,…,AnB2n-1,An+1B1,An+2B2,…,A2n-1·Bn-1交于点O，则有：

此推广命题的证明与偶数边形命题推广类似，留给感兴趣的读者完成.

根据上述推广知，平面四边形及五边形中有：

(平面四边形中的塞瓦定理)如图7，在四边形ABCD中，AC交BD于点O，E,F,G,H分别是AB,BC,CD,DA边上的点，且EG,FH交于点O，则有：

图7

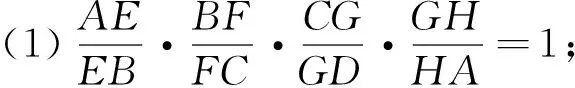
图8

(平面五边形中的塞瓦定理推广)如图8，在五边形ABCDE中，F,G,H,I,J分别是线段AB,BC,CD,DE,EF上的点，且AH,BI,CJ,DF,EG交于点O，则有：

另外，“边分比”性质及其推论在解答各类竞赛题中的也是一把“好手”，应用非常广泛.

图9

例8 (2018年山西省预赛)如图9，圆内接四边形ABCD中，自AD的中点M，作MN⊥BC，ME⊥AB，MF⊥CD，N,E,F为垂足.证明：MN过线段EF的中点.

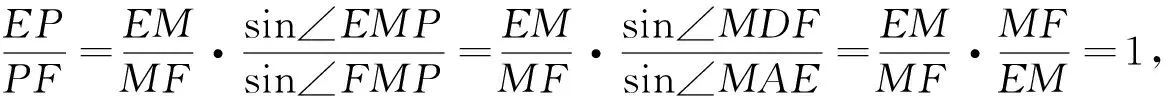
例9 (“叶军数学工作站”第78期问题研究A)如图10，已知菱形ABCD中，∠BCD=60°，E是边BC上的点，∠FBC=∠EDC，求证：A,E,F三点共线.

图10

证明：设∠FBC=

图11

例10 (2017年陕西省预赛二试)如图11，⊙O1与⊙O2相交于A,B两点，直线PQ是两圆距离点B较近的公切线，且分别与⊙O1、⊙O2切于点P,Q.设QB,PB的延长线分别交AP,AQ于点C,D，求证：AC·BC=AD·BD.

三角形“边分比”性质及推论简捷对称，模型结构简单优美，对于一些涉及长度、角度、三点共线等问题时可以考虑利用这一定理及推论来解决问题.定理的应用十分广泛，笔者水平有限以及限于篇幅，在此不再一一列举，感兴趣的读者可以继续探究.