数形巧妙结合 多角度破解一道向量问题

浙江省越州中学 (312000) 刘立锋

平面向量作为高中数学中的一个重点与热点问题，在各类考试中一直以方法多样、思维各异、能力齐全的形式呈现出来．而在破解平面向量问题时，要合理利用其自身“形”的思维或“数”的因素，结合“形”的转化或“数”的运算来分析与处理，从而达到解决问题的目的．

1．问题呈现

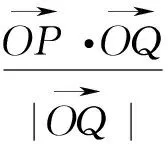
此题以平面几何为问题背景，借助平面向量的数量积与模的比值关系来确定相应的取值范围问题．破解的基本思维可以分为：正确识图，借助平面向量的“形”的思维来处理——几何角度解决；合理转化，利用平面向量的“数”的运算来解决——代数角度解决．

2．问题破解

破解视角一：几何角度

方法1：数量积定义法

从平面几何图形角度切入，结合平面向量夹角的取值范围，利用平面向量的数量积的定义加以合理转化，进而利用三角函数的图象与性质来确定相应的取值范围．

图2

解析：根据题目条件可知，点O在以AC为直径的单位圆P上(实线部分，不包含直径AC的两端点)，如图2所示.

方法2：四点共圆法

从平面几何图形角度切入，结合四点共圆的判定以及点的运动范围来确定|OQ|的取值范围，再结合平面向量的数量积以及对应几何量的关系来转化，从而得以确定相应的取值范围．

图3

方法3：投影法

从平面几何图形角度切入，结合所求代数式的几何意义，利用平面向量的投影，并结合平面几何性质和勾股定理的应用，利用点的运动特殊来确定PH的最值，从而得以确定相应的取值范围．

图4

解析：根据题目条件可知，点O在以AC为直径的单位圆P上(实线部分，不包含直径AC的两端点)，如图4所示.

破解视角二：代数角度

方法4：坐标法1

借助平面直角坐标系的建立，以点C为坐标原点，从坐标这一代数角度切入，并设出点O(x，y)，通过确定点O的轨迹方程，并利用平面向量的数量积的坐标表示以及模的公式的应用加以转化，进而化简，并利用参数所满足的条件来确定相应的取值范围．

图5

解析：以点C为坐标原点，CA、CB所在的直线分别为x轴、y轴建立平面直角坐标系，如图5所示，则A(2，0)，B(0，2)，P(1，0)，Q(1，1).

方法5：坐标法2

图6

解析：以点O为坐标原点，OA、OC所在的直线分别为x轴、y轴建立平面直角坐标系，如图6所示.

破解视角三：特殊位置角度

方法6：特殊值法

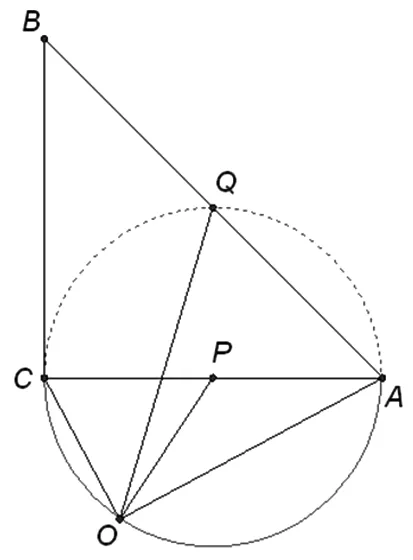
图7

解析：根据题目条件可知，点O在以AC为直径的单位圆P上(实线部分，不包含直径AC的两端点)，如图7所示.

3．解后反思

破解平面几何的相关问题，往往可以利用几何角度、代数角度、特殊位置角度等不同思维切入，实质就是充分利用平面向量的“形”的思维与“数”的因素，有针对性地从“形”与“数”的角度加以展开，正确做到“数”“形”结合，“数”“形”转化，达到多角度思维，多方法处理，从而养成学生各方面的思维品质，提升数学能力，拓展数学应用，培养数学核心素养．