探析数学建模思想在高等数学教学中的应用

赵青波

（三门峡职业技术学院，河南 三门峡 472000）

数学建模思想主要是通过对代数、函数等数学题目依据其内在发展规律，在脑中形成所学数学知识的相关模型，根据具体的数学题目套用其模型，在理解题目条件的基础上将数学模型运用到解答当中，进而帮助学生更好地理清思绪、整理思路，进一步掌握数学知识的实际应用。

一、数学建模思想

数学建模包括模型准备、模型假设、模型建立、模型求解、模型分析、模型检验、模型应用几个过程。数学建模是数学知识和实际生活的必要联系，通过数学建模可将高等数学知识的抽象性特点融入现实生活，也可以把数学问题和现实问题相结合，利用数学知识解决实际问题。数学建模本身是通过模型的建立将复杂的问题转化为简单的数学求解，通过掌握复杂问题的规律和内涵，抓住问题的关键。

在建立实际问题的数量关系和数学结构中，利用直观的数学公式来解决问题，其数学知识解决问题的过程就是数学建模思想的体现。数学建模思想具有较高的实用价值，包含了创新、应用、实践、转化和模型化的特点。在创新方面，利用数学建模在解决问题的时候对解题思路进行创新，对解题结果、问题应用等进行全面分析，需要学生具备扎实的数学基础知识[1]。在应用方面，能够将学到的数学知识、解题方法用于解决数学问题，即“学以致用”。在实践方面，将数学理论知识和实践联系起来是实践意识的体现，数学建模思想将理论性知识和实践意识结合起来，强化、论证数学知识的实用性，激发学生对学习数学知识的兴趣。在转化方面，转化意识是数学建模思想的重要组成部分，也是将实际问题转化为数学问题的关键。通过数学问题、建模、实际问题的结合，将生活性语言转化为数学问题，将复杂的问题简单化，简单的问题图像化。在模型化方面，从实际问题复杂的条件里过滤出有用的条件，通过建立模型求解，得出具有普遍性意义的结论。

二、在高等数学教学中融入数学建模思想

（一）数学建模思想对于高等数学的促进作用

高校高等数学的教学不仅要让学生掌握复杂的数学概念、公式和研究结论，还要在教学环节中融入对数学知识学习方法的教学，让学生认识到高等数学的魅力，进而了解数学知识的发展和学生对于数学知识、数学文化的掌握程度[2]。高等数学的教学既要做到对实用性知识的教学，又要注重提升学生的创新意识、应用意识、转化意识和应用能力，对高等数学进行开放性的教学，切忌固步自封。学生在开放性的高等数学教学环节中有计划地开展对知识的学习，体现了数学知识对学生今后发展起到的促进作用。

将数学建模案例融入到高校的高等数学教学中是高校高等数学未来的发展方向之一。在高等数学教学中积极融入数学建模思想能切实提高其教学效率。师生通过对高等数学建模思想的学习可以减轻实际工作与学习中的负担，学生在数学建模思想的影响下更容易理解高等数学的知识内容，有效避免了只对定义和概念这些硬性理论教学的枯燥感。通过融入数学建模思想，让学生对高等数学有一个结构性的认识，能够从被动性学习转化为自主性学习，充分激发学生学习的积极性，进而提高学生的学习效率。

（二）在高等数学教学中融入数学建模思想的原则

1.分清主次

在高等数学教学中融入数学建模思想的原则之一就是要分清主次，对高等数学中的基础性理论知识和实际应用的关系要处理好。高等数学课程是为理工科学生学习专业性知识提供的技术性数学工具。因此，对高等数学的教学要确保数学建模思想在高等数学教学当中的升华。以理论知识为基础，实际应用为目的，通过数学建模思想的支持完成对基础性知识的创新和拓展[3]。

2.灵活应用

灵活应用要求数学建模思想的融入和应用不能死搬硬套，将建模思想和高等数学教学内容有机结合起来，将数学体系与不同的数学建模联系起来，加强高等数学知识的实用性。在高等数学教学中融入数学建模思想不能一味地追求整体性的体系建立，要避免篇幅冗长。高等数学教材的内容方面并不是越多越好，而是通过科学的知识体系，使学生能够合理安排自己的时间，灵活地使用数学建模思想解决问题。

3.循序渐进

循序渐进是在高等数学教学中融入数学建模思想的重要原则之一。在高等数学教学中融入数学建模思想要使用恰当的方法将两者融合[4]。在初期的高等数学教学中融入数学建模思想要尽量涉及简单的问题，对一些简单、直观的高等数学知识点进行讲解之后，可以在学生理解的基础上教给其数学建模思想。学生在刚接触数学建模思想的时候，需要以自身已经掌握的数学知识为基础，验证数学建模思想的实用性和可行性，进而认识到建模思想的优势。随后，在数学知识的选择上逐步从简单向困难及复杂的知识转变，由浅及深适当地融入数学建模思想，让学生在潜移默化中掌握对数学建模思想的应用。

4.因材施教

因材施教是我国教育事业广泛应用的教育原则，在高等数学的教学工作中同样适用。实际的教学工作中，不同的学生具有不同特点，学生之间的差异性导致千篇一律的数学建模案例并不能满足不同学生学习高等数学知识的需求。因此，在教学工作当中要因材施教，开展学生差异化的现代化高等数学教学。其中，注重对贴合学生生活和学习的数学建模思想案例的收集，以和学生专业密切相关的数学建模思想案例引起学生的关注，激发学生对高等数学知识的学习兴趣[5]。

5.有针对性地进行教学

有针对性地开展教学工作能够充分发挥数学建模思想的资源性价值。针对高等数学课程的核心内容和重要公式进行重点讲解，注重对建模思想的引入，将创新意识和核心概念、理论相结合，倡导学生从不同的角度思考问题，进而强化对学生创新性思维能力的培养，让其针对实际问题和数学问题能够提出自身独特的见解，培养具有主观思想能力的优秀学生群体。

6.简明扼要

简明扼要也是在高等数学教学中融入数学建模思想的重要原则之一。高校高等数学的教学中对基础性概念、定义、公式讲解之后，直奔主题，将数学建模思想讲解给学生。让学生明白教师在教学当中融入数学建模思想的实际用途，进而能够将数学建模思想运用到知识的解答环境中。在教学时，教师对实际背景和应用领域内容也要进行简单清楚地表述，使学生在问题的分析上向利用数学建模思想解题方面靠拢，不在一些

不必要的条件、细节上浪费时间。

三、在高等数学教学中融入数学建模思想的教学案例

在高等数学教学中融入数学建模思想对负责教学的教师专业性能力和素质提出了较高的要求，要求教师具备宽广的知识面，能够将两者有机地结合在一起，让学生在采用数学建模思想解决问题的过程中能够认同高等数学的应用特点。

（一）案例分析

有一动点，要过河运动到位置O，其方向沿O目标不变，求该动点的游动曲线。

对该问题的解答可以将其转化成数学问题，以数学建模思想结合高等数学的知识进行解题。

对模型进行假设：

1）将河流两岸模型化，示意为平行线，河宽h；

2）动点游动速度b，河水流动速度a，且a，b为常数

3） 动点初始位置以A表示

4） 动点游动方向以O不变。

具体模型建立如图1 所示，以O 点为坐标点，将河岸以x 轴平行方向为顺水方向，y 轴为河对岸示意。

由图1所示，题目“求该动点的游动曲线”是求互P 点坐标对于时刻（t）的表达式即可。此题可以看出，动点游动轨迹受河流流速影响，为一条平滑的曲线。通过数学建模之后，学生将题目中有用的信息提炼出来，将其转化为微分方程计算，进而将复杂的题目简单化，以高等数学的相关理论知识进行解题：

T时刻动点速度为：

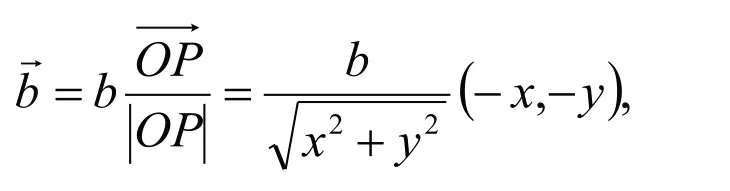
计算河流流速为 ，由此可求出动点的整体速度为

通过<1>和<2>解微分方程进而获取最终答案。

（二）代表性案例当中数学建模思想的融入

在高校的高等数学教学中，在知识概念的学习当中融入相应的经典案例能加深学生的印象，能帮助学生在实际的问题教学中提炼问题的有用信息。比如，在对函数极限学习过后，高等数学教材的联系关系中提出了“存款的问题”，要求学生用函数极限的知识内容解答问题。学生利用数学建模的学习方式，将存款问题转化为具体的函数极限运算问题，将复杂的问题简单化，加深学生对习题的理解程度。

例如：某机构在邮局购进报纸以进行零售，其进价0.5元，售价1元，在结束工作后可将为卖出报纸以0.2 元价格退回，分析如何安排购进数量，以确保实际利润最大。

对该案例的分析和解决上要考虑到市场的变化，将市场的实际需求量概率融入到题目当中，进而以数学建模思想对题目进行分析：

设每天购进n份报纸满足需求，此时平均收入为G，设报纸市场需求量为r的概率f（r），以循序渐进的思想考虑问题。

由题上条件可得：

（式中“a”为报纸购进价格、b 为实际售出价，c为退回价格、r为市场实际需求，n为购进报纸数量。）此问题主要在于将实际中的经济利益问题以数学建模思想转化为数学问题，假设a、b、c量为已知，建立f（r）和G（n）的相应方程，将f（r）方程转化为P（r）的概率密度函数：

将从而得到：

要求收入最大时，n必须满足此题中n 在卖完和未卖完中概率比P1/P2=卖出一份和退回一份（a-b）/（b-c）。建模设需求量的服从均值500 分方差50 份正态分布，得出a-b=0.5，a-c=0.3，P1/P2=5/3， 。通过查阅对应表格得到。总体上来算，当每天购进516 份报纸时，其可获取最大的收入G，约为23.48。

在此案例的分析中，通过运用数学建模思想，锻炼学生的实际创新能力，以贴近生活的经济类案例，激发学生对学习高等数学的兴趣。

四、结束语

综上所述，通过在高等数学教学中融入数学建模思想，将贴近生活的案例融入教学，引导学生采用数学建模的方式来解决贴近生活的案例问题，促进教学相长，进而切实提高高等数学教学的效率和质量。