基于谱聚类和矩阵分解的改进协同过滤推荐算法

2练林明郭芷柔

(1.广西大学计算机与电子信息学院， 广西南宁530004；2.广西多媒体通信与网络技术重点实验室， 广西南宁530004)

0 引言

个性化推荐主要通过预测用户对产品的喜好程度进而为用户推荐最合适的产品，帮助用户在海量信息中高效准确地做出决策，提高用户满意度。目前常见的推荐算法有基于内容的推荐算法、基于协同过滤的推荐算法、混合推荐算法等[1]。其中，基于协同过滤的推荐算法[2]主要依据特定的机器学习算法得到较好的推荐效果，其核心思想是利用用户和产品之间的互动信息进行推荐，多数情况下为用户评分矩阵。但在现实应用中，往往出现只有少数用户会对产品进行评分的情况，推荐算法无法为那些评分信息甚少或者没有的新产品进行推荐，因此协同过滤算法存在新产品冷启动[3]、数据稀疏性等问题。对此，本文提出了一种融合谱聚类[4]和矩阵分解的混合推荐算法。首先使用基于随机梯度下降优化求解的矩阵分解方法，将原始矩阵分解为较低维的用户特征矩阵和特征产品矩阵[5]，然后使用谱聚类算法根据产品外部属性信息对产品进行聚类获得聚类簇以及簇内产品的相似度，最后根据相似产品及其相似度，以及相似产品的特征向量之间的关系，计算新产品的特征向量，进而完善原有的特征产品矩阵。

1 相关工作

在基于矩阵的协同过滤推荐研究方面，矩阵分解最初采用的是奇异值分解(singular value decomposition, SVD)[6]，但是由于这种分解方式需要预先对评分矩阵中的缺失值进行补填，评分矩阵因此会由稀疏矩阵变成稠密矩阵，且计算复杂度高，故其实用性不强。后来提出了Funk SVD算法[7]等改进，其基本思想是将原始矩阵分解为两个低维的特征矩阵，并采用均方根误差(root mean square error, RMSE)衡量原始矩阵和分解后的矩阵的误差，若可得到最小的RMSE差值即可以找到最接近原始矩阵的分解矩阵，由此矩阵分解问题则转化为求最小误差的问题。常用的矩阵分解方法如交替最小二乘法(alternating least squares, ALS)，其优点是求解过程中需要优化的参数易于并行，在非稀疏数据集上的求解速度较快，不足是求解过程中的逆矩阵计算在当样本数量特别大的时候需要消耗大量的时间。因此，这方面的工作关注如何选择合适方法进行误差函数的优化。另一方面，个性化推荐算法往往需要采用聚类算法，通过不同的聚类思想，将数据划分为多个部分，使得每个部分内部的数据相似性[8]最高。

而融合聚类和矩阵分解的协同过滤算法已有相关研究。文献[9]提出一种基于用户和产品双聚类的协同过滤推荐算法，虽可改善数据稀疏性带来的影响，但对于初始矩阵中不存在的新产品无法进行合理的推荐。文献[10]提出首先利用KMeans聚类对产品、用户分别聚类，然后将对原始评分矩阵的分解转变为对由相似用户和已评价的产品及其相似产品组成的评分矩阵的分解计算。李改等[11]提出使用KNN算法对产品的特征和属性进行映射，然后综合相似产品和相似度填充产品特征矩阵。董立岩等[12]首先利用ALS算法对矩阵进行分解，然后再利用改进的k-均值聚类算法对补全好的矩阵建立聚类模型进行推荐。它们可在一定程度上解决产品冷启动问题，但其都是针对产品属性元素较少的产品进行分类或者聚类，而对于属性元素较多的产品来说，KNN和KMeans在计算复杂度上较高、计算时间较长。填充评分值虽然可以缓解评分矩阵的稀疏性，但不能准确体现用户对未知产品的喜爱程度，而且回填后的评分矩阵由稀疏变得稠密，对系统的存储空间提出较高要求，也不利于对评分矩阵后续的预测处理。

2 改进的协同过滤推荐算法

本文在聚类和矩阵分解的协同过滤算法的改进思路为：首先使用基于随机梯度下降优化求解的矩阵分解方法，将原始矩阵分解为较低维的用户特征矩阵和特征产品矩阵，进而预测用户对产品评分的近似值，上述过程解决了数据稀疏性和求解速度问题，但是没有考虑到由于用户对新产品不存在历史评分行为而产生的冷启动问题，故引进产品外部属性信息，使用谱聚类算法根据产品外部属性信息对产品进行聚类获得聚类簇以及簇内产品的相似度，最后根据相似产品及其相似度，以及相似产品的特征向量之间的关系，计算新产品的特征向量，最后填充特征产品矩阵。算法的基本过程如下：

① 初始化用户特征矩阵U和特征产品矩阵V；

② 对用户特征矩阵U和特征产品矩阵V进行迭代更新，每次更新使用训练集中的一条数据。当迭代次数足够多或者最近两轮迭代的RMSE误差变化范围小于设定阈值时结束迭代；

③ 通过谱聚类算法得到每个新产品对应的相似产品；

④ 得到新产品的特征向量并回填通过步骤②得到的特征矩阵；

⑤ 根据矩阵U、V获得预测评分矩阵R，其中R=U×VT；

⑥ 针对不同用户根据评分的TopN原则进行推荐。

其中，主要过程主要包括分解原始矩阵、谱聚类求解产品特征向量、填充特征—产品矩阵等步骤。

2.1 分解原始矩阵

基于矩阵分解的协同过滤推荐算法是将矩阵分解问题转化为求最小误差的问题。设将具有m个用户、n个产品的用户—产品评分矩阵记为Rm×n，其中，R(i,j)表示用户ui对产品vj的打分情况。假设将矩阵Rm×n分解为矩阵Um×k和Vk×n，要使得矩阵Um×k和Vk×n的乘积能够近似接近评分矩阵，即满足：

(1)

假设用P代表U中的元素，用Q代表V中的元素，则矩阵R的元素的值为：

(2)

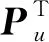
如果可得到这样的矩阵U、V，使得对于已知评分的估计误差最小，便可以通过矩阵U、V预测未知的产品评分，此时误差即为：

(3)

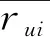
则得误差函数如下：

(4)

对误差函数，先对U矩阵中的点进行随机梯度下降算法求解：

(5)

其中，Puk是矩阵U上的数据点。

继续化简得到：

(6)

(7)

同理得：

(8)

式(7)、式(8)即为目标函数在矩阵U和矩阵V上的梯度。假设学习率为η，则可得到更新后的Puk和Qki的值为：

Puk=Puk-η(-2euiQki)=Puk+2ηeuiQki,

(9)

Qki=Qki-η(-2euiPuk)=Qki+2ηeuiPuk。

(10)

在得到基本的更新函数后，本文需要考虑模型是否会出现过拟合现象。为了避免产生过拟合，需要对误差函数加入正则化项，即：

(11)

则可以根据按梯度负方向更新得到Puk和Qki的值为：

Puk=Puk+2η(euiQki-λPuk),Qki=Qki+2η(euiPuk-λQki),

(12)

其中，η为学习率，eui为当前预测误差，λ为防止过拟合系数。

2.2 谱聚类求解产品特征向量

谱聚类求解产品特征向量基本过程如下：

① 使用高斯核函数对引进的产品外部特征矩阵进行处理，获得相似矩阵S；

② 构建相似矩阵S的邻接矩阵W和度矩阵D，其中邻接矩阵和度矩阵都是对称矩阵；

③ 构建拉普拉斯矩阵L，L=W-D；

④ 采用基于权重的NCut切图方式[13]，将图分割为k个子图，单个子图的NCut公式表示为：

(13)

对于k个子图，可以表示为：

(14)

其中，tr(HTLH)为矩阵的迹，且有HTDH=I。

接下来采用维度规约近似求解H，将图的切割转换成求解拉普拉斯矩阵特征值(向量)的问题，并计算其各自对应的特征向量f，k个特征向量组成n×k维的特征矩阵，即为所需要的H。

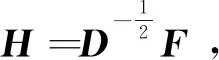
(15)

⑤ 将由k个特征向量组成的特征矩阵H采用式(16)按行标准化，获得n×k维的特征矩阵F：

(16)

⑥ 取F中的每一行作为一个k维的样本子集，一共有n个这样的子集。通过K均值聚类对新样本集进行聚类，聚类数为k2。

⑦ 获得最终的簇划分C=(c1,c2,c3,…,ck2)。

2.3 填充特征—产品矩阵

使用谱聚类算法对产品聚类，然后根据相似产品及其相似度权重回填特征产品矩阵，其中相似性度量采用标准的余弦公式[14]。回填值相关计算公式如下：

(17)

(18)

其中，φf(xvi)表示的新产品i的第f个特征值，xvi代表新产品i的属性向量，sim(xvi,xvj)则表示与新产品i相似的已知产品j之间的相似度，由式(17)计算得到，而hij则为已知产品j的第f个特征值，通过随机梯度下降算法得到。

3 实验

本文以智慧旅游应用中的景点推荐作为场景进行实验，使用的数据主要来源于使用八爪鱼数据采集器获得的“去哪儿网”旅游网站(https://piao.qunar.com)中的数据，其中包括用户对旅游景点的评分数据以及旅游景点信息介绍。由于爬虫爬取的数据往往含有不完整、不正确或不相关的脏数据，本文在采集数据后对相似重复数据进行了数据清洗[15]。对于景点评分数据，理论上来说，用户评分越高，其对该景点越为喜爱，即用户对景点的评分是对景点喜爱程度的直接体现。数据集的基本信息如表1所示。

表1 用户—景点评分数据集Tab.1 User-attraction rating data set

由表1可知，用户—景点评分数据集的数据稀疏性达到0.064，由数据稀疏性的定义可以得到，大部分用户对景点的评分数据都为空，所以这个数据集是非常稀疏的。本文从数据集中随机抽取80 %的数据作为训练集，剩下20 %的数据作为测试集，训练集包括全部用户对1 631个景点的评分，测试集中包括29个训练集中未出现的新景点，且每个新景点在测试集中至少有一条评分数据，所有新景点的评分数据为34条。

引进的产品外部属性信息为景点文本信息，主要包括1 660个文档，每个文档描述了对应景点的相关信息，通过利用jieba中文分词、TF-IDF算法，可以将景点文本信息转换为景点特征矩阵，该矩阵是一个高维稀疏矩阵。

实验采用均方根误差RMSE和平均绝对误差MAE作为评价指标，主要通过计算实际评分与预测评分之间的误差衡量混合推荐算法的准确性，即误差值越小，推荐算法的准确度越高，预测评分越接近真实评分，推荐结果越能符合用户真实兴趣。实验环境为PC机(Intel Core i5-7500处理器，8 GB内存，500 GB硬盘)；Windows10操作系统；编程语言为Python 2.7。

首先，比较通过融合不同聚类算法解决协同过滤算法的冷启动问题，将K均值聚类算法和本文使用的谱聚类算法进行比较，对使用K均值聚类算法与本文协同过滤算法在聚类时间、准确度等性能上进行对比。SGD_KMeans由于在谱聚类算法的实现过程中，选取高斯核函数求解特征矩阵的相似矩阵，所以需要进行调优的参数包括高斯核函数中的gamma值和聚类簇数(本文对于分割图数k1和聚类簇数k2取值相同)。实验证明，gamma在取值为1.0，聚类簇数k取值为15时，谱聚类算法性能趋于稳定；聚类簇数k取值为15时，K均值聚类算法性能趋于稳定，且聚类簇数对算法性能影响较小。由于谱聚类算法在聚类过程中利用了降维操作，因此相比较KMeans聚类算法，谱聚类对于高维度的稀疏数据具有很好的适用性，计算复杂度相对较低，特别适合文本聚类情况下使用，如表2所示。

表2 不同聚类算法的优化性能对比Tab.2 Comparisons of optimal performance of different clustering algorithms

表2中，SGD_KMeans算法使用K均值聚类，SGD_SC算法使用谱聚类。由表2可以看出，在高维度的景点特征矩阵下，KMeans的聚类时间要远远大于谱聚类所需要的时间，几乎是谱聚类算法聚类所需时间的10倍；在推荐算法的准确率上，谱聚类算法与K均值聚类的准确率相差不大。由此可以看出，在基于聚类和矩阵分解的个性化旅游景点推荐技术中，使用谱聚类的优化效果要优于传统的K均值聚类。后文实验中，主要采用基于谱聚类算法优化的协同过滤推荐算法进行性能对比。

基于矩阵分解的协同过滤算法的核心思想是将原始矩阵通过降维技术，分解为两个低维度的特征矩阵，其中特征矩阵的特征数对算法整体性能具有影响：特征数太小，影响推荐算法的准确率；特征值过大，又需要大量的存储空间来存储特征矩阵。因此选择合适的特征数对推荐算法具有直接的影响。通过对比不同特征数下未优化的协同过滤推荐算法、使用均值填充和使用谱聚类算法进行优化后的算法性能变化情况，其中原始协同过滤算法标记为SGD[16]，使用谱聚类算法进行优化的协同过滤算法标记为SGD_SC，使用均值填充的改进协同过滤算法标记为SGD_AVG，图1和图2分别展示了3种算法的RMSE、MAE值。

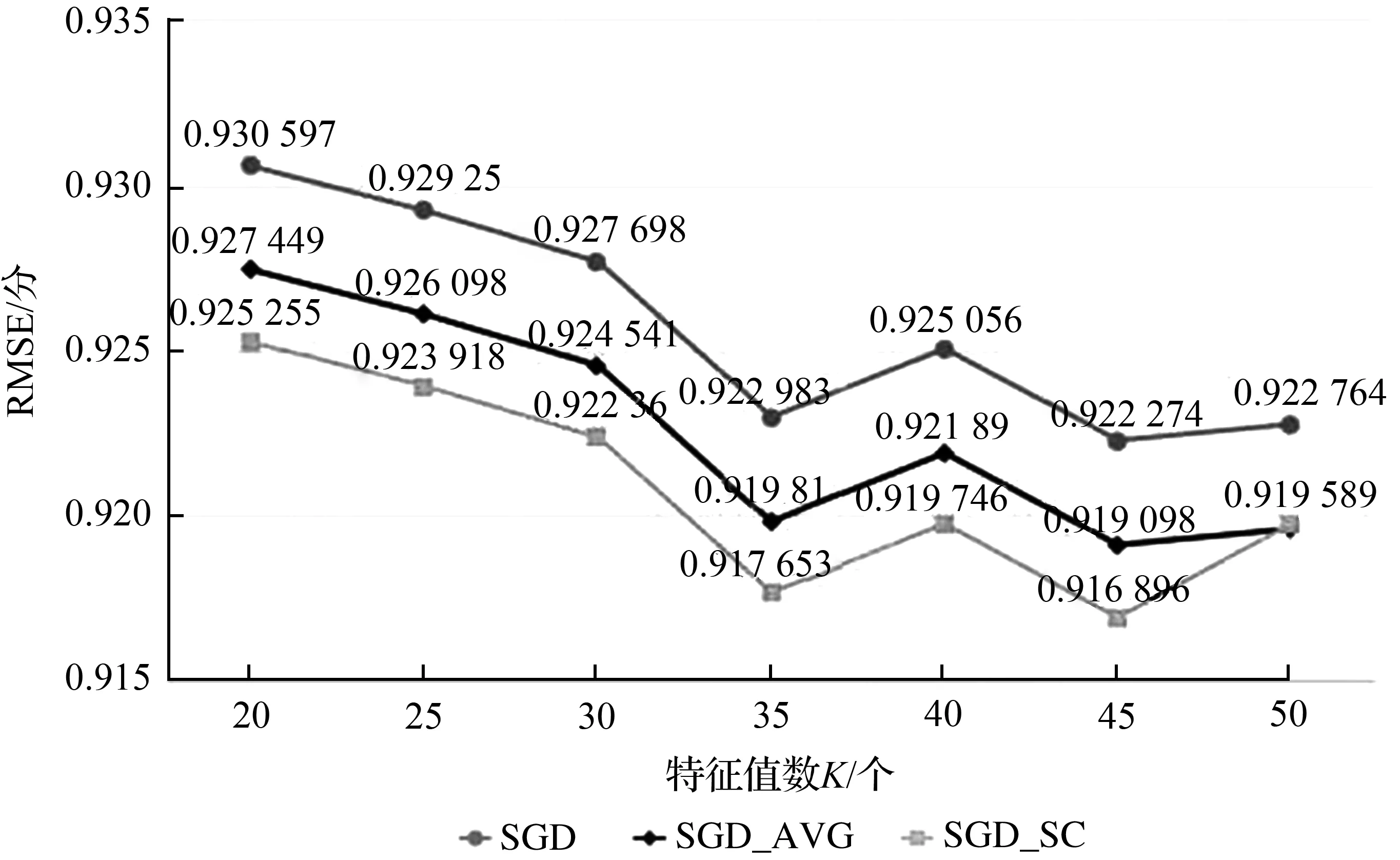
图1 不同特征值数下各算法的RMSE误差对比Fig.1 Comparisons of RMSE of each algorithm under different characteristic values

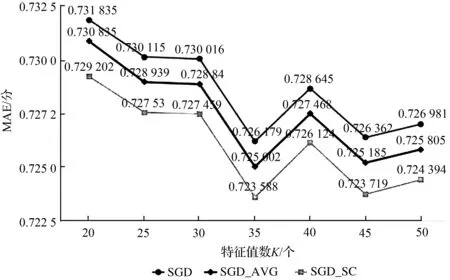
图2 不同特征值数下各算法的MAE误差对比Fig.2 Comparisons of MAE of each algorithm under different characteristic values

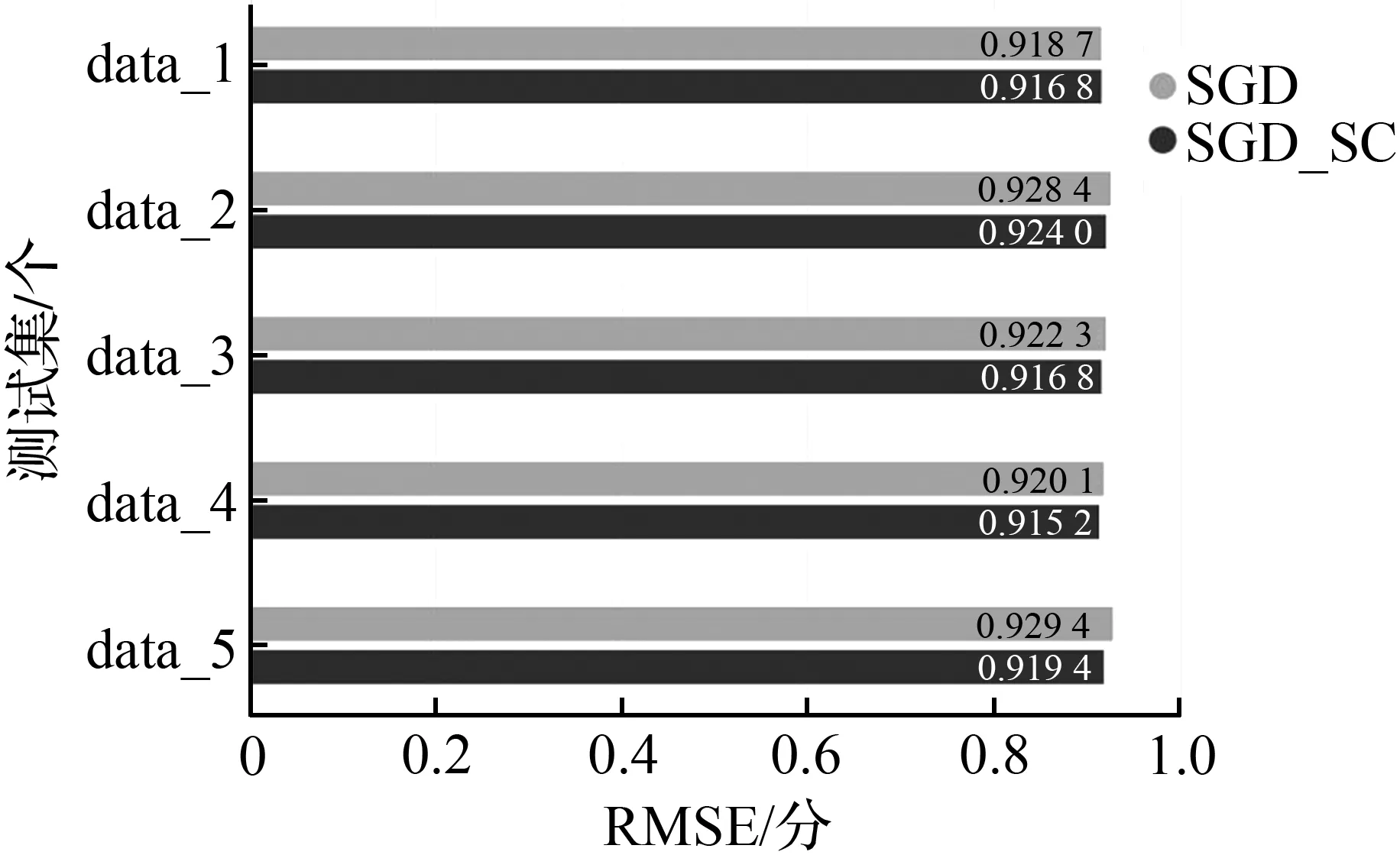
图3 不同新景点评分点数量下模型误差变化情况对比Fig.3 Comparisons of model error changes under different number of new attractions

由图1和图2可以看出，特征值数取45时算法性能基本达到稳定。与未优化的原始算法对比，使用均值填充进行优化的协同过滤算法和使用谱聚类算法进行优化的协同过滤算法都在一定程度上降低了模型误差，提高了算法性能，且使用谱聚类算法进行改进的效果更加明显。随着特征值数量的不断增大，SGD_AVG算法、SGD_SC算法和原始的SGD算法性能均趋于稳定。

根据新景点的数量不同，对比使用本文算法和原始协同过滤算法的在解决冷启动问题的效果变化情况，对比5组数据(data_1～data_5)，结果如图3所示。

其中新景点的数量以及对应的评分点数量情况如表3所示。

表3 新景点以及对应的评分点数量情况表Tab.3 New attractions and corresponding score points

根据测试集中所包含的新景点数量及其评分数量的不同，对原始数据集进行5次不同的数据分配，具体分配情况如表3所示。由图3和表3可以看出，新景点数量越多时，使用谱聚类优化的协同过滤推荐算法与原算法之间的预测误差对比越明显，即推荐模型的改进效果越好。

本文提出的融合谱聚类算法的改进协同过滤算法，可以有效地解决新景点冷启动问题。与传统的采用K均值聚类改进的协同过滤算法相比，谱聚类的聚类时间更短，更适合旅游景点文本聚类；与使用均值填充改进的协同过滤算法相比，基于谱聚类的协同过滤算法准确度更高。

4 结语

本文提出了一种基于谱聚类的改进个性化协同过滤推荐算法，针对推荐系统存在的数据稀疏性和冷启动问题，采用基于矩阵分解的协同过滤方法作为基础方法，将谱聚类算法与其相融合，并根据对比实验分析证明改进后的算法与传统基于K均值聚类改进的协同过滤算法等相比能有效提高推荐结果的准确率，较好地解决新产品的冷启动问题。下一步工作改进思路主要包括考虑通过对原始评分矩阵中的用户和产品进行联合聚类，进一步缓解数据稀疏性和减小矩阵分解计算量；增大对比实验力度，提升算法适用性。