薄壁支架零件加工变形分析*
赵夫超 雷小宝 刘 畅 鲍满腔
(1安庆职业技术学院机电工程系;2安庆市鼎润智能装备制造有限公司 安徽安庆 246005;3安徽大学电气工程与自动化学院 安徽合肥 230601)
薄壁支架零件由于质量轻,具备特殊的材料性能等特点被广泛应用在航空航天工业中。很多薄壁支架零件采用的材料多为铝合金、钛合金等材料,薄壁支架零件的外部轮廓尺寸与截面尺寸相比偏大,加工余量大,会使得它的刚性差,在加工过程中会出现严重振动,从而影响零件的加工精度与表面质量。薄壁支架零件在加工过程中很容易产生加工变形,这已然成为机械加工中的一大难题,因此开展薄壁支架零件的三维建模,加工变形仿真分析具有十分重要的意义。
目前,国内外很多学者针对薄壁件加工变形方向有不少研究,同时也取得了一定成绩。如Wun Ling,Lai Zone Ching Lin 等通过模拟正交切削实验[1],得出一些很重要的规律,零件的变形大小取决于应力分布状况,零件的应力分布状况又受到刀具参数的影响,即选择不同参数的刀具会导致零件的变形程度不同。另外,针对具体的薄壁支架零件的加工,S.Smith等人研究了零件整体刚性对切削加工质量的影响,研究结果表明采用提高刚性的措施可达到有效减轻薄壁支架类零件的加工变形,提高产品质量与生产率[2];国内南航的王志刚等详细研究了薄壁零件的加工变形过程,他假设材料在加工过程中一直处于弹性范围,主要考虑了切削力作用下对薄壁零件产生的弹性变形,但是没有考虑到其他因素对变形的影响[3];而北航的Wang Zhao jun等利用有限元软件模拟了材料去除对薄壁零件加工变形的影响,但是他在分析过程中忽略了切削力的作用[4];浙大的黄志刚等对引起变形的因素进行了详细的分析,他们建立了金属正交切削加工的切削力与切削热相互影响的模型,对加工变形的原理进行了广泛深入的研究[5]。
文章在对薄壁支架零件的三维建模与结构功能分析的基础上,采用模拟切削仿真方法,分析了引起薄壁支架零件加工变形的因素,对导致加工变形的主要切削力影响因素进行了具体分析。
1 薄壁支架零件的三维建模
基于Solidworks软件,建立薄壁支架零件的三维模型,由图1可见,该薄壁支架零件安装被支撑件处壁厚较薄,此处刚性较差,在加工过程中受到各种因素的耦合作用容易产生变形。

图1 薄壁支架三维模型
2 薄壁支架切削加工切削力分析
薄壁支架零件加工过程复杂,一般在数控铣床上完成加工。由文献可知航空铝合金7075-T745在立铣刀进行铣削加工时的铣削力经验模型[6],见公式1。
(1)
式(1)中,Fx、Fy和Fz分别为铣削力在x、y和z三个方向上的分力,ap为铣削深度,ae为铣削宽度,v为铣削速度,f为进给量。在加工过程中以Z端面为研究对象,在铣削时使用整体硬质合金直柄立铣刀,分粗铣,精铣两个过程。
文章切削仿真先选取Z端面的凹槽进行切削力有限元分析,在上面的计算过程中优先选取以下切削用量:v=1600m/min,f=0.2mm/r,ap=0.5mm,ae=0.8mm来计算切削力。
3 薄壁支架切削加工变形有限元仿真
3.1 加工变形有限元仿真
(1)利用三维软件Solidworks建立薄壁支架零件的几何模型。文章所研究的薄壁支架零件的尺寸为86mm×86mm×70mm。
(2)添加材料库与模型的材料属性。选用铝合金7075-T745,设置弹性模量E=113Gpa,泊松比u=0.33。
(3)添加边界条件。所加工的铝合金薄壁支架零件Z面添加约束,上部及两端处于自由状态。首先只考虑铣刀在某个位置时的情况,此时切削力处于铣削槽面上,力的大小可借助于上述创建的切削力经验模型进行计算,在有限元分析模型的区域上施加载荷[7],仅仅研究与加载垂直方向加工表面上的力Fz。

f0.0022=38.1N,此时最大的总变形为2.7167e-6,如图2所示。

图2 Fz=38.1N时Total Deformation
3.2 仿真结果分析
通过采取有限元办法对铝合金薄壁件加工变形的模拟分析,可以得到以下几点结论:
(1)用Ansys对铝合金薄壁支架零件加工变形进行仿真分析,其分析结果与实际加工情况具有较高的拟合度,预测结果可有效用于薄壁支架类零件加工前的工艺优化设计。
(2)沿薄壁支架零件的高度方向,高度不断增大,欠切量随之增大;在刀具进给方向,薄壁支架零件的最终切削厚度也呈现出较大的加工误差,这些是由零件不同位置的刚度存在较大差异所导致的。薄壁零件加工时让刀变形与切削点的刚度具有较大关系,切削点的刚度越小,该处的欠切量就会越大。所以,如何有效提高切削点的刚度是工艺优化设计工作的重要研究内容[8]。同时可以据此来优化数控铣削工艺,根据有限元分析的欠切量适当的进行刀具补偿,可以有效地减小薄壁件加工过程中的变形。
(3)切削三要素进给量、背吃刀量和切削速度的减小都有利于切削力的减小,其中背吃刀量影响最大,进给量次之,切削速度最小。但是本零件为薄壁支架零件,切削温度会造成热变形,很大程度影响切削加工质量,切削热受切削速度影响最大,进给量次之,背吃刀量最小。所以切削时的切削用量选取要重点控制进给量,且在整个切削过程中持续冷却液冷却。
4 基于有限元仿真的切削加工变形规律预测
4.1 一般模型的建立与有限元仿真
上述内容对加工该薄壁零件Z面时的切削加工变形进行了有限元仿真,最后对仿真结果也进行了分析。现在为了得到一般性的切削加工变形规律,需将对上面的切削加工过程进行简化处理,再建立一般的模型,然后对简化的模型进行有限元分析,最后依据所得数据进行规律预测。
(1)首先将加工对象简化成扇形薄板件,如图3所示。
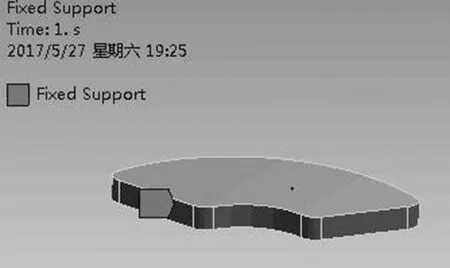
图3 简化的扇形薄板模型
(2)通过前面的计算取Fz=47.7N,按照图4所示的节点逐点施加Fz,得出每个节点处的总变形云图,其中某一个节点处的处理结果如图5所示。
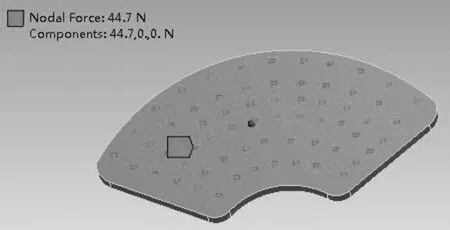
图4 切削力施加节点示意图

图5 某一节点处总变形云图
(3)按照前面的处理过程,在图4所示的节点处依次施加力,得到如5所示的总变形云图,记录数据,按照节点位置径向大小对数据(取三组数据为例)进行分类统计,可以做出R相等时各节点的总变形曲线,如图6~图8所示。
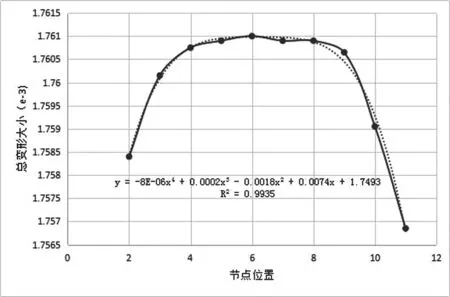
图6 R=30mm的节点总变形曲线

图7 R=24mm的节点总变形曲线
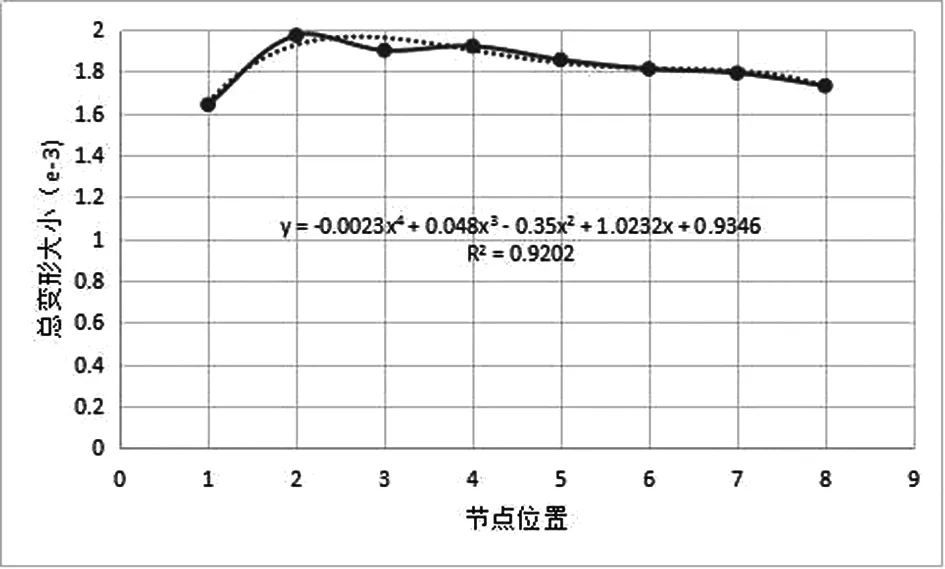
图8 R=18mm的节点总变形曲线
4.2 切削加工变形规律预测
对图6~图8中曲线用最小二乘法拟合可以得到其近似曲线,通过各R2的大小可以发现拟合结果较好。可以看出,在R相同时,各个节点的总变形量满足四次多项式:y=ax4+bx3+cx2+dx+e。对于扇形模型来说,其中每个节点均用极坐标:(R,θ)唯一确定,这样总变形量就可以表示成θ的函数,即D(θ)=aθ4+bθ3+cθ2+dθ+e(其中a,b,c,d,e与R有关且由R唯一确定)。
为了得到径向的变形规律,现将各个R相等时的各个节点处的总变形求平均值,可以得到图9所示R变化时节点处总变形曲线,同样采用最小二次法对曲线进行拟合,可以得到一个四次多项式函数,将其用极坐标表示即:D(R)=aR4+bR3+cR2+dR+e(其中a,b,c,d,e均与θ有关且由θ唯一确定)。
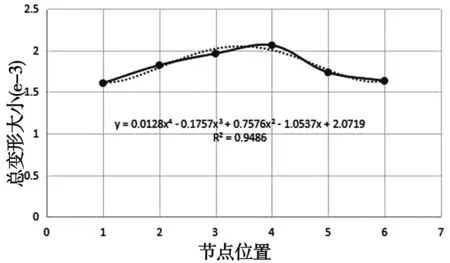
图9 R变化时节点处总变形曲线
综上可知,对于这样的扇形模型,在周向或径向,可以用极坐标(R,θ)通过四次多项式来表示总变形量的大小。通过建立一般模型,分析有限元仿真结果及建立数学模型,可以预测切削加工总变形量规律。
5 小结
针对薄壁支架零件加工质量难以控制的问题,在分析了国内外研究现状的基础上,利用有限元分析方法,对某三轴飞轮集成支撑架进行了三维建模及加工变形分析,得出结论如下:
(1)分析引起薄壁支架零件加工变形的因素,对导致加工变形的主要因素切削力进行了分析;
(2)简化了薄壁支架有限元模型,对所加工面进行节点划分,仿真分析加工过程中每一节点的实时变形状态,建立各节点变形数学模型,预测了加工变形规律。

