一体化通信基站风振响应及风振计算研究

史国富 屠海明

(同济大学建筑设计研究院集团(有限)公司 上海 200092)

引言

一体化通信基站是近年来逐渐兴起的一种新型通信基站，其主要组成部分由通信铁塔、通信机房、基础配重三部分组成，通信铁塔通常采用单管塔加斜撑的结构形式，通信机房采用钢框架及彩钢板围护，基础配重为混凝土条形梁。该三部分集成为一体，所有构件均为工厂预制，现场拼装，无需开挖土方、浇筑混凝土，其施工质量可控，安装拆卸快捷迅速，占地面积小，便于移动搬运，可灵活布置基站，对于工艺规划布点有着很强的适用性，近年来得到了广泛的应用。

由于天线、微波等附属物挡风面积较大的特点，控制设计荷载为风荷载。规范通过风振系数来考虑脉动风的影响，然而其体型不同于常规的高耸悬臂结构体系，外形尺度变化较大且为非规则变化，《建筑结构荷载规范》(GB50009-2012)[1](以下简称为规范)规定的风振系数计算方法需在进一步假定的基础上使用。本文通过对风荷载数值模拟，对一典型一体化通信基站进行了风荷载时域风振响应分析，得到了相应高度的风振系数，并与基于规范的两种近似计算方法进行比较分析，为该类型的通信塔结构风振计算提供参考。

1 工程概况

一体化通信基站高度35m，标高15m处设置支撑，悬臂高度20m。主体结构采用钢管，钢材材质Q345B，图1a、b中支撑构件规格为φ168×8，塔体共分为六段，塔段01、02构件规格为φ480×12，塔段03、04构件规格为φ480×14，塔段05、06构件规格分别为φ402×12、Φ351×8；基础采用预制混凝土条形梁基础以抵抗整体倾覆力矩，塔体与基础通过底部转换钢梁连接为整体。结构设计基本风压0.55kN/m2，地貌类别B类，共设置3层天线，每层设置3副天线支架，每副天线及RRU挡风面积不超过0.65m2。结构如图1所示。

图1 一体化通信基站Fig.1 Elevation view of integrated communication base station

2 风荷载时程模拟

2.1 脉动风速功率谱密度函数的选取

我国荷载规范采用Davenport提出的顺风向脉动风速功率谱密度函数[2]。其表达式为：

(1)

2.2 脉动风荷载功率谱密度函数矩阵

基于Davenport谱，根据Bernoulli定理，采用Gauss模型忽略脉动风速平方项，可导出脉动风压功率谱；并考虑高度、体型、迎风面积等因素对风荷载的影响,可得到各质点处脉动风荷载的自功率谱密度函数；考虑脉动风的竖向相关性,从而得到作用在不同高度处的脉动风荷载互功率谱密度函数。脉动风荷载{Fi}的功率谱密度函数最终可以用矩阵表示为[3]：

[S{Fi}(ω)]=[Spi]Sf(ω)

(2)

式中:[Spi]为功率谱密度函数系数矩阵;Sf(ω)为归一化脉动风速功率谱。系数矩阵中i、j列元素为：

Spipj=coh(i,j)σw(zi)σw(zj)AiAj

(3)

(4)

式中：coh(i,j)为脉动风荷载竖向相干函数;σw(zi)为结构第i个质点处脉动风压的标准差;Ai为结构第i个质点处迎风面积;μf(zi)为脉动系数;μs(zi)为结构体型系数;μz(zi)为风压高度变化系数;g为峰值因子;w0为基本风压。

2.3 谐波合成法模拟脉动风荷载

风荷载模拟的方法主要有两类：一类是基于三角级数叠加的谐波合成法，另一类是线性滤波器法。本文采用谐波合成法，用一系列具有随机频率的正弦、余弦函数序列来对风荷载进行模拟。设模拟时需要拟合的功率谱矩阵为复共轭矩阵[S(ω)]，且[S(ω)]具有Hermite性质。按照Cholesky分解法，[S(ω)]可分解为：

[S(ω)]=[H(ω)][H*(ω)]T

(5)

式中:[H(ω)]为下三角矩阵。

根据多维随机过程样本模拟的理论，采用谐波合成法模拟的随机过程具有如下形式[4]：

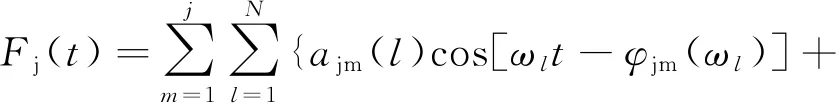
(6)

采用上述方法进行风荷载模拟时，N应充分大以避免周期性存在，频率区间[ωa,ωb]应足够大以包含脉动风中高阶频率成分对结构的影响，时间步长应足够小(Δt≤π/ωb)以避免风荷载模拟过程中高频成分被过滤掉。

2.4 风速时程模拟样本

结合本工程实际，模拟了高度6m、12m、15m、18m、23m、29m、32m、35m处共8条风速时程曲线。以18m处为例，其风速时程及自功率谱密度曲线如图2所示。

图2 18m处风速时程及自功率谱密度曲线Fig.2 Time-history curve of wind and PSD at 18m height

通过对比分析风速时程样本的功率谱密度函数可以看出，模拟谱的走势与目标谱较一致。

3 一体化通信基站时域风振响应分析

3.1 分析模型及动力特性

本工程分析采用专业有限元软件SAP2000进行空间建模整体分析，杆件均采用梁单元，顶部天线支架及天线作为附加质量作用于相应节点[5]。模态分析采用Ritz向量法，提取前6阶的自振周期和振型见图3。

由模态分析结果可知，前6阶振型均为x、y向平动，y向刚度弱于x向，因此后续时程分析风荷载加载方向采用y向。

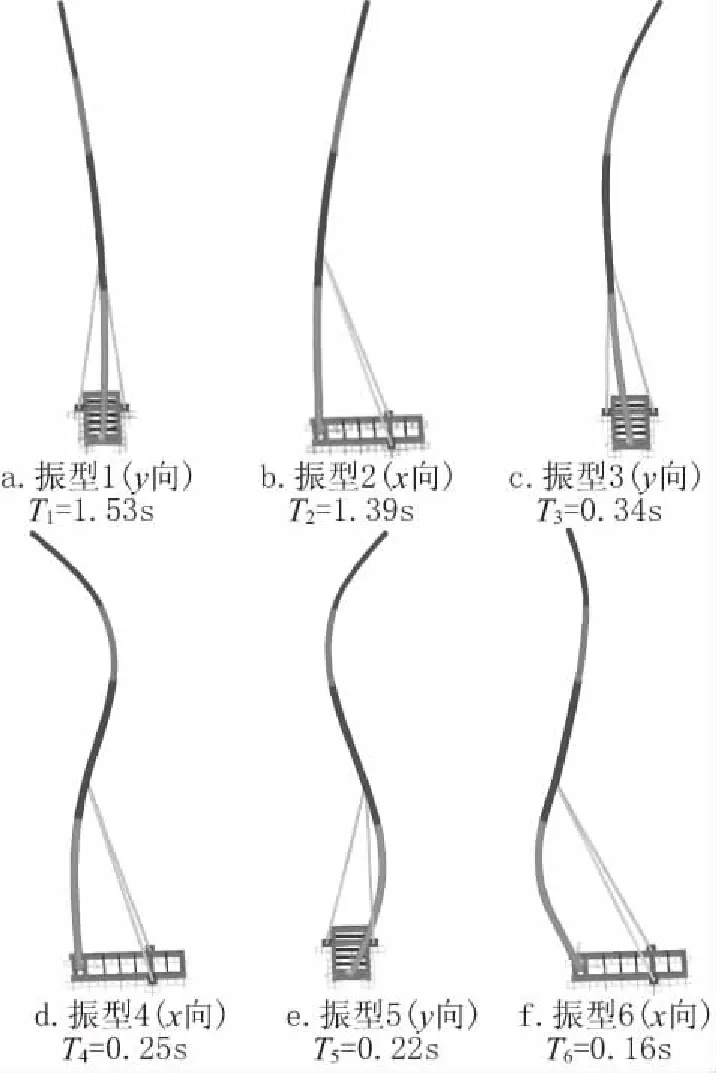
图3 各阶振型及周期Fig.3 Modal shape and period of each order

3.2 风振响应分析

将所模拟的各高度处风荷载时程曲线施加于模型相应节点处，分析工况采用瞬态动力时程分析，时间积分列式采用NewMark-β法。以18m处节点为例，提取该处节点位移、加速度时程曲线如图4所示。

图4 标高18m处节点动力响应Fig.4 Dynamic response at 18m height

图5 节点动力响应统计值Fig.5 Node dynamic response statistics

对各节点速度、加速度的风振响应时程分析统计结果见图5。由图5分析结果可知，在标高15m(斜撑处)以下结构动力响应较小，在15m以上悬臂处位移均值、标准差、加速度标准差均随高度增加较快，动力响应明显。

4 一体化通信基站风振系数

4.1 时域风振响应分析风振系数

我国荷载规范对于脉动风荷载所引起的动力响应采用惯性力法(IWL)考虑，根据风振系数的定义，由时域风振响应分析结果根据式(7)可得各高度处相应风振系数[6]：

(7)

式中:mz为z高度处集中质量；ω1为结构一阶圆频率；σyz为z高度处的位移均方差；μs为体型系数；μz为z高度处风压高度系数；Az为z高度处迎风面积；g为峰值因子，取2.5；w0为基本风压。

4.2 规范法分析所得的风振系数

对于悬臂型结构，具有低阻尼和稀疏阵型频率的特性，第一振型的影响一般起绝对作用，规范风振系数从结构动力方程出发，用结构的一阶振型惯性力来表示，公式表达以风振系数与平均风的乘积得到等效静风荷载。

由于一体化通信基站其体型的特殊性，在实际设计中通常采用两种方法近似计算。第一种计算风振系数时假定按塔柱外形考虑修正系数，不考虑斜撑的外形影响，振型系数根据结构动力计算确定。本文称此方法为整体悬臂法。第二种仅悬臂段以上考虑风振影响，假定其嵌固于斜撑顶部，悬臂段以下刚度较大不考虑风振影响,计算风振系数时同普通悬臂高耸结构。本文称此方法为顶部悬臂法。

4.3 计算结果对比分析

采用上述方法分别得到风振系数如图6所示，结构位移如图7所示。比较可知在高度23m以下时域分析法所得风振系数均大于规范法，在高度29m、32m、35m处时域分析法所得风振系数显著小于规范法，并且小于23m处风振系数，这主要是由于所挂载天线挡风面积较大、质量较小，导致惯性力与静风载的比值较小所致。规范法计算风振系数时未考虑沿塔高质量与面积的突变，因而其沿高度变化均匀，无突变。

从位移比较图7中可以看出，整体悬臂法计算结果最大，偏于保守，时域分析法最小，顶部悬臂法介于二者之间。

图6 风振系数比较Fig.6 Comparison of Wind-induced vibration coefficient

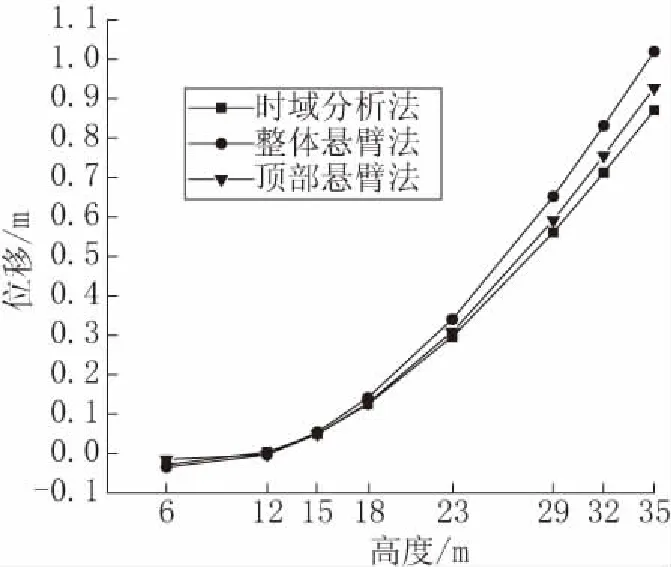
图7 位移比较Fig.7 Comparison of displacement

与时域分析法相比，其顶部位移整体悬臂法偏大17.1%，顶部悬臂法偏大6.5%。与时域分析法相比，顶部悬臂法无需较为复杂的风荷载模拟和基于随机振动理论的有限元分析，相对而言计算简便，具有较好的精度，且能包络时域分析值，可满足实际工程设计需要。

5 结论

本文基于Davenport风谱，采用谐波合成法实现了对风荷载的模拟，对一体化通信基站的时域分析，得到了各节点的位移、加速度响应。通过对响应时程曲线的统计分析，采用惯性力法求得相应高度处的风振系数，并与基于规范的近似计算方法整体悬臂法及顶部悬臂法的结果比较分析，可得出如下结论：

1.从各节点的位移、加速度响应统计分析值可知，比较而言顶部悬臂段振动明显，其动力响应远高于底部支撑部分。

2.比较不同的分析方法可知，时域分析法所得风振系数在高度23m以下均大于规范法，顶部挂载天线处存在突变，小于规范法。规范法沿高度变化均匀，无突变，与时域分析法相比，其顶部位移整体悬臂法大17.1%，顶部悬臂法大6.5%。

3.尽管随机振动理论的时域分析法其精度较高，可考虑各阶振型对结构动力响应的贡献，但由于脉动风的模拟及分析过程较为复杂，在实际工程设计中难以普遍采用，基于规范风振系数的顶部悬臂法其计算精度可满足工程需要，在实际设计中可采用此近似计算法。