既有铁路两侧护栏的加固方法及数值模拟研究
毕继红 叶弘罡 霍琳颖 赵云 王照耀
(1.天津大学建筑工程学院 300350;2.滨海土木工程结构与安全教育部重点实验室(天津大学) 300072)
引言
铁路工程快速发展,其两侧通常设有护栏,然而因为工作时间增长以及环境因素的影响,整体结构出现老化,承载力大幅度地降低,带来严重的安全隐患,亟需加固。
为提高既有结构的承载力,相关学者提出许多加固方法,并进行了大量的试验和理论研究[1,2]。其中,工程水泥基复合材料(Engineered Cementitious Composites,ECC)是一种常见的加固材料[3,4],被广泛应用于钢筋混凝土结构的补强和抗震加固。相关学者进行了大量研究[5-7]。胡世翔[8]等进行ECC增强钢筋混凝土梁与普通混凝土梁加载试验,通过对比试验结果发现,普通混凝土梁加入ECC之后,破坏形式从剪切破坏、局部压坏等脆性破坏变为延性破坏,并且ECC增强钢筋混凝土梁的裂缝宽度较小,抗剪承载力、延性系数均大于普通RC梁。崔涛[9]等通过ECC连接的直剪构件与整浇构件加载试验的对比,发现ECC可以有效地承载剪力作用,对构件的表面进行键槽处理可以有效地提高连接效果。并且,通过对加载过程的研究,给出了剪切承载力的计算公式,可以较好地描述破坏规律。周开富[10]等通过对15根不同配筋、不同高度的ECC加固RC梁进行四点弯曲试验,发现ECC与RC梁粘结良好,在加载下可以产生协调变形,满足平截面假定。ECC通过改善RC梁的开裂程度有效地提高了承载能力,并且配筋率越小,改善程度越高。
上述研究表明,采用ECC对既有结构进行加固可以有效地提高承载能力。但是,现有研究和工程中通常将ECC当做一种现场施工材料,而现场施工环境复杂,施工质量难以保证。本文将ECC制成工厂预制板(以下称为高韧性水泥板),研究高韧性水泥板对于护栏的加固方式、加固效果和加固机理。
1 加固方案及试验概况
1.1 加固方案
未加固护栏为钢筋混凝土结构,示意见图1a。加固方案是在未加固护栏左右两侧用水泥砂浆粘贴高韧性水泥板,并用螺栓加固。高韧性水泥板为工厂预制板,材料为掺加了聚乙烯醇(PVA)纤维的ECC,并在背面做了凹凸状处理,加固后护栏如图1b所示(高韧性水泥板和砂浆从左向右依次标为1号、2号、3号)。

图1 加固前后护栏示意Fig.1 Schematic diagram of the guardrail before and after reinforced
1.2 试验概况
以加固后护栏为试验体进行了加载实验[11],加载点位置、监测点位置、边界条件见图1b,试验所用各种材料物理性能见表1和表2。

表1 混凝土和高韧性水泥板材料参数Tab.1 The material parameters of concrete and high toughness cement board
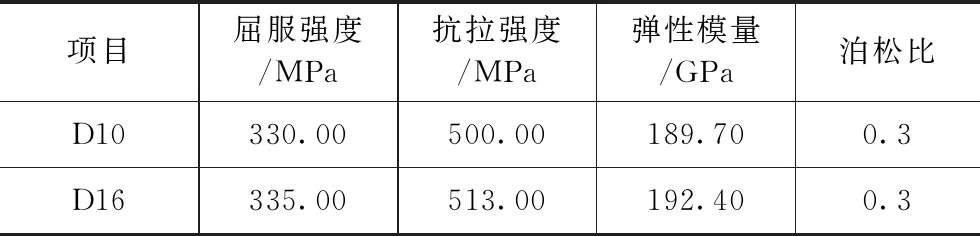
表2 钢筋材料参数Tab.2 The rebar material parameters
注:D10和D16分别为直径10mm和16mm的带肋钢筋。

图2 加载装置Fig.2 Loading device
试验采用单调位移加载,为了防止加载处出现应力集中,导致混凝土压碎,在试件和加载装置的接触处设置尺寸为500mm×30mm×15mm的钢垫板,同时在加载处设置位移计,测量试件的变形,加载装置如图2所示。
2 有限元模型
2.1 有限元模型的建立
如图3所示,利用ABAQUS软件建立了加固后护栏的有限元模型。有限元模型Z轴方向仅截取500mm的计算长度,X和Y方向采用原有试验模型尺寸。其中,混凝土、高韧性水泥板、水泥砂浆、加载板和支座垫板均采用八节点六面体单元(C3D8R),钢筋采用两节点线性三维桁架单元(T3D2),钢筋和混凝土之间使用Embedded功能实现分离式建模,混凝土、高韧性水泥板和水泥砂浆之间采用Tie功能进行结合。

图3 有限元模型Fig.3 The finite element model
2.2 加载和边界条件
有限元分析时采用位移加载,将位移施加在加载板中心外侧15mm的参考点处,而参考点和加载板的上表面进行了所有自由度的耦合,使得荷载均匀施加在模型上,避免应力集中而导致计算结果不精确甚至不收敛。此外,基础末端采用固接。
2.3 本构模型
在有限元模型中,混凝土选用损伤本构模型[12],其单轴本构关系选用《混凝土结构设计规范》[13]所给的混凝土应力-应变曲线,如图4所示。fc,r、ft,r分别代表混凝土抗压、抗拉代表值,εc,r、εt,r分别代表抗压、抗拉极限强度对应的应变。

图4 混凝土单轴应力-应变曲线Fig.4 Uniaxial stress-strain curve of concrete
有限元模型中,钢筋采用较为经典的线性强化本构模型[14]:
(1)
式中:σs为钢筋应力;εs为钢筋应变;εy为钢筋屈服应变;fy为屈服应力;Es为钢筋弹性模量;E″s为钢筋强化模量;εs,u为钢筋极限应变。
(2)
式中:fs,u为钢筋极限应力。
有限元模型中高韧性水泥板采用Han[15]提出的ECC本构模型,受拉时的应力-应变关系为:
(3)
式中:σcr、εcr分别为出现开裂时ECC的应力、应变;σtp、εtp分别为峰值应力及其对应的应变;εtu为极限拉应变;E0为初始弹性模量。
受压时的应力-应变关系为:
(4)
式中:σcp、εcp分别为峰值应力及其对应的应变;εcu为极限压应变。
3 有限元模型验证及结果分析
3.1 荷载-位移曲线对比
如图5所示,通过对比试验与有限元分析得到的荷载-位移曲线可以发现,在弹性阶段,两者曲线基本重合,高韧性水泥板和钢筋受力均较小,这一阶段的极限称为比例极限,对应的荷载称为初裂荷载。试验中初裂荷载为13.32kN,数值模拟得到的初裂荷载为12.58kN,两者相差5.56%。试验与数值模拟初裂荷载对应的位移分别为1.21mm和1.10mm,两者相差9.09%。

图5 荷载-位移曲线Fig.5 The load-displacement curve
荷载继续增大,构件进入到塑性阶段。裂缝不断开展,混凝土强度开始下降,钢筋和高韧性水泥板的应力不断增大,结构的整体刚度不断减小,最终达到荷载-位移曲线的峰值。试验中极限荷载为31.11kN,数值模拟得到的极限荷载为32.40kN,两者相差3.98%。试验与数值模拟极限荷载对应的位移分别为6.51mm和5.81mm,两者相差10.75%。
从上述分析中可以发现,数值模拟结果与试验结果吻合较好,初裂荷载、极限荷载和其对应的位移之间的误差均较小,证明了本文有限元模型建模方法的有效性及准确性。
3.2 护栏混凝土最大主应力分析
在初裂前,主要是混凝土承担荷载,处于弹性阶段,混凝土变截面处和护栏底面处受拉,如图6a所示。随着荷载不断增加,受拉区的高度逐渐增大,混凝土最大主应力逐渐增大,监测点位移U=1.10mm时,混凝土底部截面处开裂,如图6b所示。随着加载位移的增大,混凝土受拉区继续扩大,裂缝越来越多,钢筋的应力越来越大,U=5.58mm时,钢筋屈服,如图6c所示。U=5.81mm时,护栏底面处混凝土已经形成贯穿裂缝,达到极限荷载,如图6d所示。
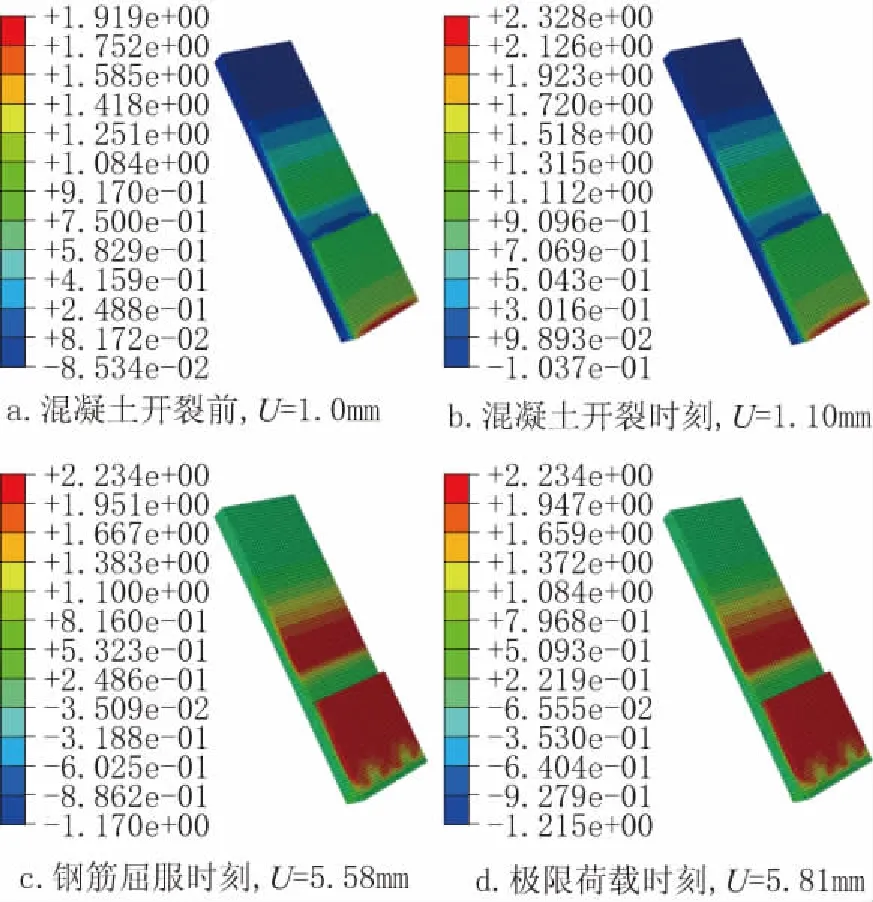
图6 加固后护栏混凝土部分应力云图(单位:MPa)Fig.6 The stress cloud diagram of reinforced guardrail concrete(unit:MPa)
由图6分析可知,在整个加载过程中,护栏上部和下部均参与了结构的受力,主裂缝形成于护栏底部截面处而非变截面处,各部分材料性能均得到了充分的发挥。
4 加固效果和参数化分析
4.1 加固效果分析
采用上述模拟方法,计算未加固护栏在单向荷载作用下的受力性能,并与加固后护栏做了比较,分析破坏形态方面的差异,进而讨论加固后承载力提高的原因。
1.荷载-位移曲线对比分析
由图7可以看出两条曲线相差较大,加固效果显著。在弹性阶段,加固后护栏因为增加了高韧性水泥板和水泥砂浆,刚度变大。未加固护栏和加固后护栏初裂荷载分别为10.37kN和12.58kN,各自对应的位移为1.53mm和1.10mm。进入塑性阶段后,未加固护栏的荷载-位移曲线迅速达到峰值并下降,而加固后护栏有较长的裂缝扩展期。护栏经过加固,极限荷载由11.74kN变为32.40kN,提高了176%,对应的位移分别为1.82mm和5.81mm,提高了219.2%。达到极限荷载后,整体结构仍然能够保持较强的承载能力。

图7 荷载-位移曲线Fig.7 The load-displacement curve
2.加固前后护栏主裂缝对比分析
如图8所示,对比护栏加固前后主裂缝位置可知,未加固护栏混凝土主裂缝存在于混凝土上部和下部之间的变截面处,未加固护栏混凝土下部的承载能力并未得到充分的发挥,变截面处一旦破坏,整体结构就失去了继续承载的能力。护栏经过高韧性水泥板的加固,变截面得到增强,加固后护栏混凝土的主裂缝存在于底部截面处,结构作为一个整体承载,更好地发挥了结构各部的承载能力,从而提高了结构的承载能力。

图8 护栏主裂缝位置(单位:MPa)Fig.8 The main crack position of guardrail(unit:MPa)
3.加固前后护栏应力云图对比分析
图9给出了数值计算得到的极限荷载时刻未加固护栏混凝土的最大主应力云图、加固后护栏混凝土的最大主应力云图和高韧性水泥板应力云图。对比分析图9a和图9b可以发现,加固后护栏中混凝土发挥承载能力的部分明显增多,这是由于高韧性水泥板提高了结构的整体受力性能,使得更多的混凝土发挥了承载能力。对比图9b和图9c可以发现,加固后护栏底部混凝土已经开裂,而相同位置处的高韧性水泥板底部应力在11MPa左右,由于高韧性水泥板韧性较好,随着荷载的增大,高韧性水泥板的应力下降会比较缓慢。因此,高韧性水泥板在混凝土开裂后仍能发挥承载能力,使得结构继续承受荷载。
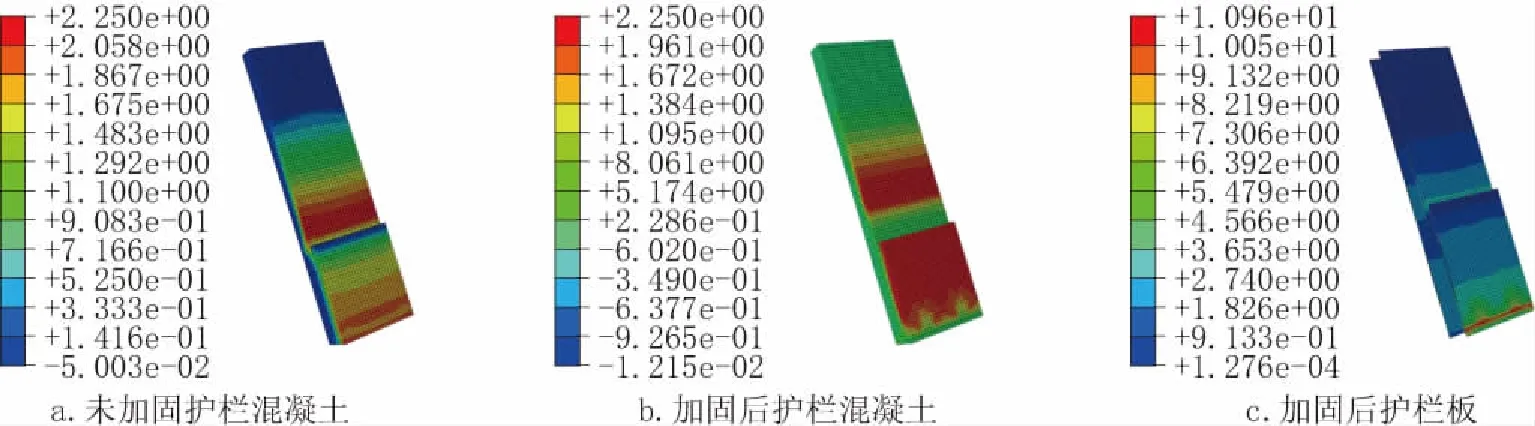
图9 护栏混凝土部分应力云图(单位:MPa)Fig.9 The stress cloud diagram of guardrail concrete(unit:MPa)
4.2 高韧性水泥板厚度分析
由于加载过程中主裂缝出现在加固后护栏中1号高韧性水泥板底部附近(即图1b最左侧板),且厚度是水泥板重要几何尺寸,也是影响护栏受力的关键因素,本节分别模拟了1号高韧性水泥板厚度为8mm、16mm、24mm、32mm、40mm、48mm、64mm、75mm、100mm的加固后铁路两侧护栏破坏过程(各个计算模型只有1号高韧性水泥板厚度变化,其他部分保持不变)。

图10 极限荷载与水泥板厚度的关系Fig.10 Correlation between ultimate load and cement board thickness
图10给出了数值模拟计算得到的1号高韧性水泥板厚度与极限荷载的关系,由图可以看出,随着1号高韧性水泥板厚度的增加,加固后护栏的极限荷载近似线性增加,厚度每增加8mm,极限荷载平均提高5.8kN。但是厚度达到48mm后,继续增大厚度,极限荷载不再增加,稳定在54.90kN左右。
4.3 高韧性水泥板高度分析
本节分别模拟了1号高韧性水泥板高度为0mm、550mm、650mm、750mm、850mm的加固后铁路两侧护栏破坏过程(因为1号水泥砂浆是用来固定1号高韧性水泥板,因此随着1号高韧性水泥板高度的变化,1号水泥砂浆的高度也随之改变,其他参数均保持不变)。
图11给出了数值计算得到的1号高韧性水泥板不同高度时,加固后护栏的荷载-位移曲线。由图可以看出高度为0mm的1号高韧性水泥板模型与其他模型的曲线完全不同,该曲线经过短暂的弹性阶段后很快进入塑性,并且极限荷载相对于弹性极限荷载并没有太大的提升。高度为550mm的1号高韧性水泥板模型虽然极限荷载最终达到了30kN以上,但是从弹性阶段结束到极限荷载经过了较长的加载阶段,极限荷载对应的位移过大。650mm及以上高度的1号高韧性水泥板模型的荷载-位移曲线整体趋势相似,虽然在弹性阶段和塑性阶段刚度略有不同,但是达到极限荷载后的曲线基本重合,各个模型极限荷载和对应的位移差别较小,加固效果相同。

图11 荷载-位移曲线Fig.11 The load-displacement curve
5 结论
本文通过使用ABAQUS软件对使用特制高韧性水泥板加固后护栏加载试验进行模拟,计算加固前后的护栏受力情况,并对高韧性水泥板的厚度和高度进行参数分析,得到以下结论:
1.建立的有限元模型能较好地模拟加固后护栏的承载过程,得到的开裂荷载、极限荷载及其对应位移与试验结果相差10%左右,误差在允许范围内。
2.高韧性水泥板在混凝土破坏后能继续承担荷载;采用高韧性水泥板对护栏进行加固将极限荷载提高了176%,对应的位移提高了219.2%,极大地提高了护栏的承载能力和韧性。
3.随着1号高韧性水泥板的厚度的增加,加固后护栏的极限荷载基本呈线性增长,而当厚度超过48mm后,加固后护栏的极限荷载不再增大,稳定在54.90kN左右。
4.当1号高韧性水泥板高度为650mm时,既能最大程度地提高护栏的承载能力,又避免了材料的浪费。

