深水功能舱悬垂安装过程动力学仿真研究

贾晓丽，爱吉木，刘书海，王 懿，彭 鹤

(中国石油大学(北京)a.机械与储运工程学院；b.安全与海洋工程学院,北京 102249)

具有水下生产系统的油气田开发模式因其节省费用，安全可靠，不受恶劣天气影响等优点，成为了深海油气田开发的主要模式[1-3]。深水油气田的水下生产系统的很多重要技术都被国外所垄断，如何突破这些垄断，建立有自主产权的水下生产系统，成为重要的课题。新一代水下生产系统(如图1)打破了传统水下生产系统的全湿式方案，创建了基于深水功能舱的全干式和半干半湿式紧凑型垂直水下布局理念[4]。功能舱在陆上制造完毕后，经运输、下放安装、调试等环节，投入生产。功能舱的下放安装过程的动力学分析是整个深海油气田开发任务中的重要环节[5-6]。

图1 新一代水下生产系统

功能舱在深海低温高压环境中工作，传统的下放安装法，例如钻杆安装法及吊机安装法不再适用[7-8]。悬垂安装法是巴西Petrobras公司针对超深海环境和较大质量设备的安装而专门设计的一种快捷、简便的安装方法，更适用于新一代水下生产系统的安装要求[9]。悬垂安装法流程如图2所示，在安装地点，安装缆索一端与功能舱相连，另一端与安装船相连。运输船用吊机将功能舱吊起，行驶一段距离，通过吊机将功能舱下放至飞溅区以下的一定深度(通常为50 m)；之后，吊机施放功能舱，因自身重力作钟摆运动至指定海底安装位置。由于功能舱受到拖曳力以及绳索和浮力模块的阻尼作用，不会作往复钟摆运动。本文把悬垂安装过程分为3个阶段，图2中1位置是开始阶段，2位置是悬垂阶段，3位置是稳定阶段[10-12]。

悬垂安装法具有成本低、适用深水、避免共振且对安装船舶要求较低，施工方便等优点。但是，其安装过程受力复杂，必须通过仿真模拟、水池试验或海上模型试验等方法验证，才能进一步提高实际工程安全性和可靠性。Petrobras公司最早采用悬垂安装法成功将280 t和200 t的管汇安装到1 845 m和1 900 m水深的位置[13]。随后，多国研究人员都对悬垂安装法进行了仿真研究。国内学者利用Fluent等软件对悬垂下放法安装耦合系统进行模拟[14-18]。然而，悬垂安装法的实际案例仍然较少。

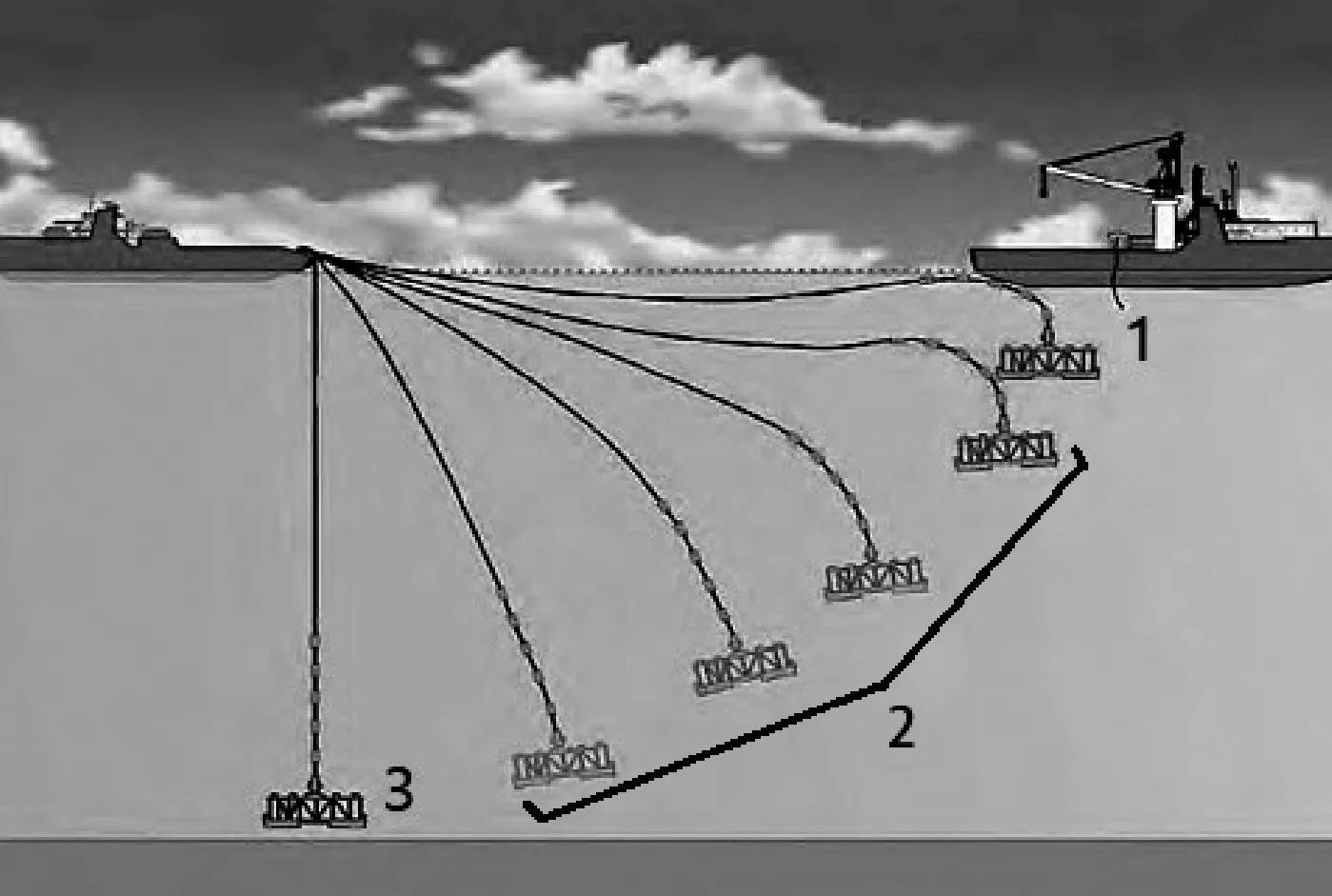
图2 深海石油生产系统中功能舱的悬垂安装过程

本文采用ANSYS-AQWA有限元软件对悬垂安装系统进行船-缆-功能舱多体建模。因安装水深不适用抛锚定位，所以采用理想化的动力定位进行安装船定位。根据DNV-RP-C205规范[19]，设立模拟海况数据作为安装环境条件[20]。通过与已发表文献进行对比，验证模型的有效性，实现新一代水下生产系统功能舱悬垂安装过程的多体三维时域耦合仿真。分析波浪有义波高、功能舱质量及功能舱重心高度等参数对下放过程中缆索张力、功能舱轨迹和姿态的影响，并对本文模型的安全性进行初步评估，研究结果可对实际工程提供一定的理论指导。

1 悬垂安装系统建模

悬垂安装系统是由安装船、缆索、功能舱组成的多体系统[21]。定义船艏柱与基线交点为坐标原点，基线沿船艉方向为x轴正方向、船体甲板垂直剖面向内为y轴正方向、以船艏柱向上为z轴正方向。以Hallin Marine公司所产的工程船为参考设计MPV(Multi-Purpose Vessel)船，船体模型的基本参数如表1所示。通过AQWA-AGS Line Plan编写AQWA型线文件，实现安装船计算模型的建立，限制安装船纵、横荡及艏摇从而模拟理想化的动力定位。编辑并读取型线文件，以其为基础建立MPV水动力学计算模型。依据本文要求，在AGS Line-Plan界面进行单元网格划分，建立吃水5.6 m、最大网格单元长度为6 m的水动力计算MPV船模型，如图3所示。

表1 MPV安装船基本参数

图3 在AQWA AGS Lines-Plan中建立的MPV船模型

因功能舱结构较MPV船简单，可以使用直接编辑功能舱dat文件的形式建立其几何网格模型。使用若干TUBE莫里森(Morison)管单元、一个PMAS质量单元和一个DISC碟形单元建立功能舱舱体结构模型。为了避免因功能舱艏摇转动导致仿真输出数据中纵摇转变为横摇，建立由8个TUBE单元组成的方框固定在模型外侧，限制功能舱艏摇运动，使得仿真结果更加准确。在功能舱dat文件中设置ZLWL水线位置卡片，并设置功能舱释放的初始位置为水面。将dat文件导入经典AQWA程序中运行，即可在AQWA-AGS Line Plan中获得功能舱几何网格模型，如图4所示。

图4 功能舱几何网格模型

缆索建模以编辑dat文件的形式完成。主要思路是使用MOOR卡片，使用COMP命令定义多成分缆，ECAT定义多个缆索的物理特性，NLID定义缆索在MPV船以及功能舱的连接点，分别连接在安装船末端以及功能舱顶端。使用LINE定义线弹性绳，使用ECAH命令定义缆索的水动力系数。船-缆-功能舱模型分别完成后均导入经典AQWA中运行，即可在AQWA-AGS Line Plan中获得悬垂安装系统几何网格模型，如图5所示。

图5 悬垂安装系统几何网格模型

2 模型验证

使用文献[22]中参数，采用上述建模思路进行建模验证。文献[22]中使用PID控制器仿真安装船动力定位。本文模型则将动力定位系统理想化。根据文献[22]，下放物体参数、缆索参数和环境载荷参数如表2～4所示，采用JONSWAP波浪谱。

表2 下放物体基本参数[22]

表3 缆索基本参数[22]

表4 波浪载荷参数[22]

使用文献[22]数据进行仿真后得到下放物体沿z轴方向速度-时间历程曲线，如图6所示。由图6可知，下放物脱离缆索2时刻，两者在z方向速度最大误差为1.4 m/s。在100 s时，时间-历程曲线基本重合。文献[22]数据在550 s后进入稳定阶段，但仍然有震荡情况产生，而模型仿真数据并没有过大的震荡产生。分析原因是由于模型将动力定位系统理想化导致的。仿真结果与对比文献中下放物z方向速度-时间历程曲线变化趋势基本相同，数据基本相符。

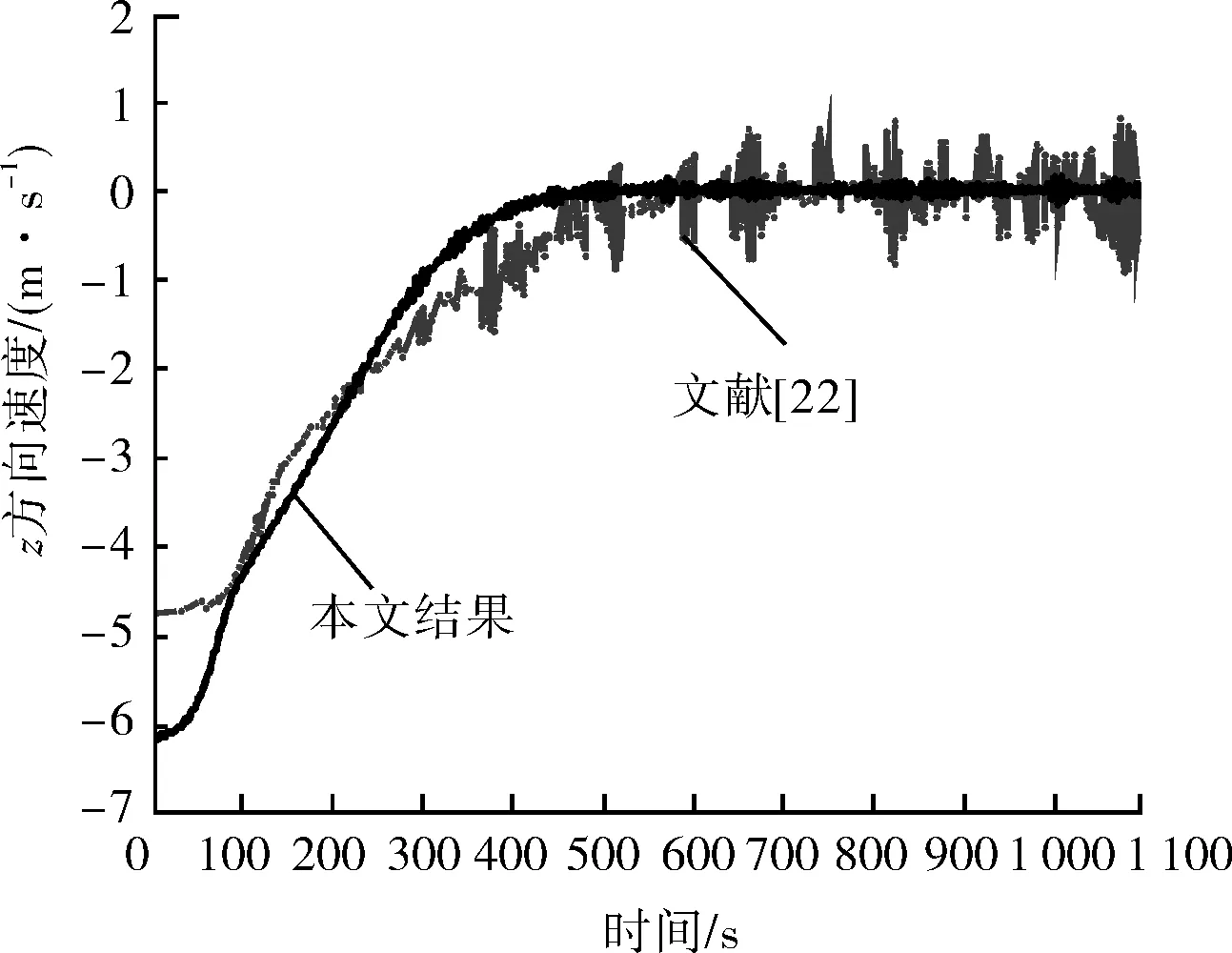
图6 下放物z方向速度-时间历程曲线

图7为下放物纵摇-时间历程曲线，仿真结果与文献[22]中下放物纵摇-时间历程变化趋势基本相同，数据基本相符。在吊放缆索解脱后，文献[22]中的数据出现较强纵摇震荡，直至170 s，而模型仿真数据中并未出现太大震荡，原因是本文模型将动力定位系统理想化导致的。

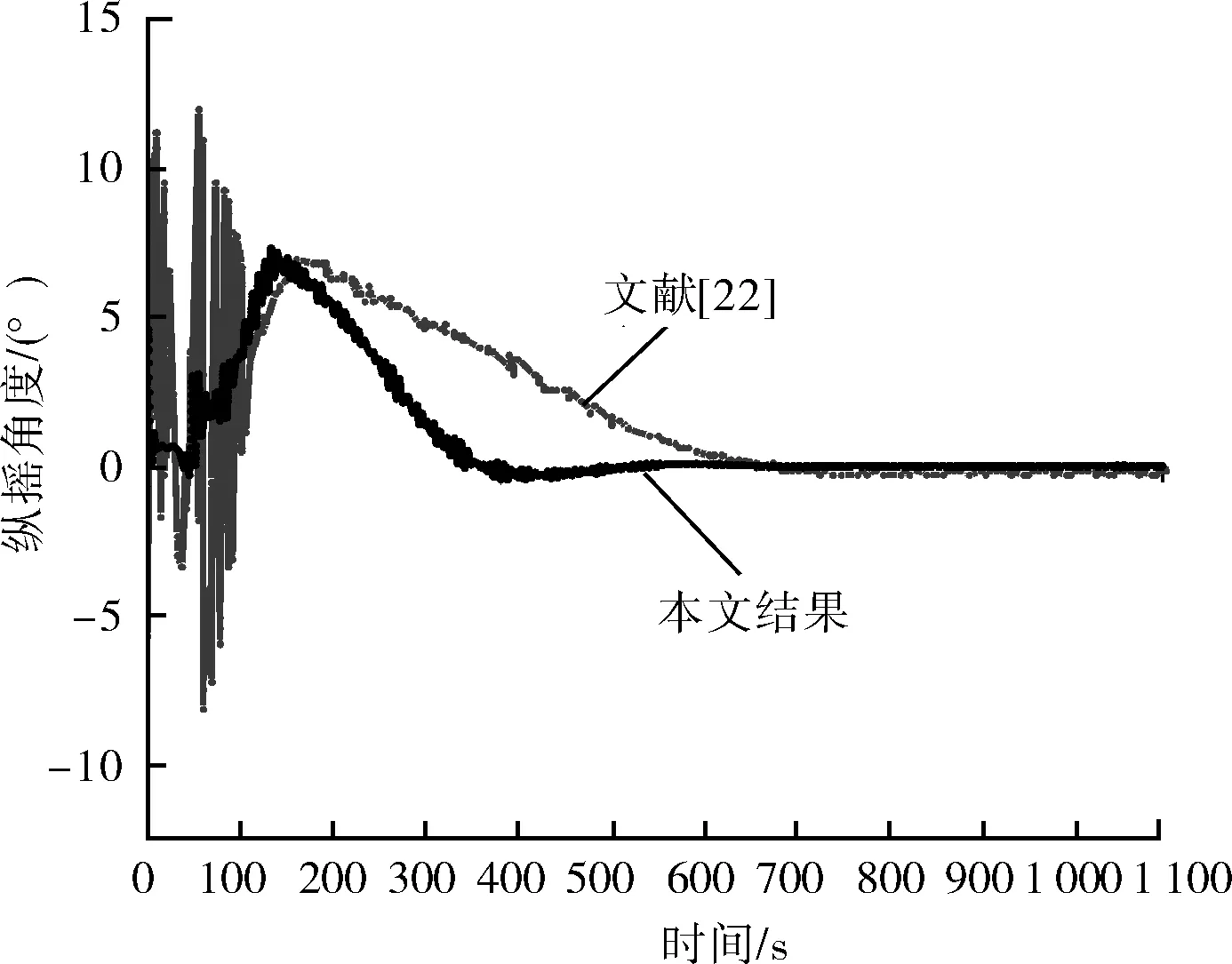
图7 下放物纵摇-时间历程曲线

图8为缆索张力-时间历程曲线。本文模型与文献[22]中缆索张力数据变化趋势基本相同，曲线基本重合，本文仿真结果与文献[22]数据相符。在稳定阶段，文献[22]数据有一定的震荡，而本文模型仿真数据震荡不剧烈，原因是本文模型中将动力定位系统理想化导致的。

综上所述，本文模型的动力定位理想化模拟对本模型和文献[22]之间的数据产生了少量的误差，但文献[22]数据与模型仿真数据基本相符，证明本文的建模方法可行，可以对功能舱的悬垂安装过程进行仿真。

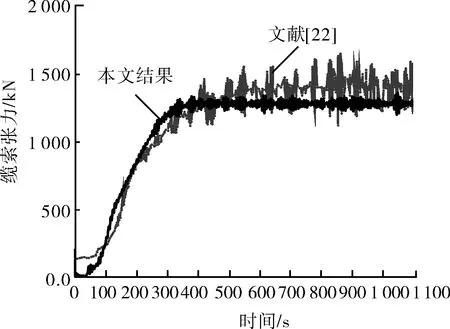
图8 缆索张力-时间历程曲线

3 数值模拟仿真

3.1 模型参数及边界条件

在确定模型可行性后，使用STRT卡片中的POS命令定义初始位置的设置，MPV船的重心在整体坐标系中的坐标为(38,0,2)，功能舱起始位置坐标为(1 380,0,-51)。计算步长和步数分别设置为0.2 s和7 000次。根据DNV-RP-C205规范，设立模拟海况数据作为安装环境条件。使用ENVR卡片中的CPRF命令对剖面流速及方向进行设置，CPRF命令支持对不同水深对应不同流速和不同流动方向的设置。因理想化了动力定位系统，所以不再对风载荷进行额外设置。使用SPEC卡片中SEED命令设置波浪种子数，波浪种子是时域分析下的波浪载荷随机性指标。使用JONH命令定义JONSWAP波浪谱。波浪载荷参数如表5所示，海流载荷参数如表6所示。

表5 波浪载荷参数

表6 海流速度

使用表7与表8参数分别确定功能舱和缆索。使用PROP卡片对仿真输出内容进行设置，PPRV命令设定输出的pos文件记录频率，PREV命令设置lis文件中输出的时域计算结果记录频率。

表7 功能舱基本参数

表8 主缆索基本参数

3.2 关键参数影响分析

图9为悬垂安装过程不同有义波高下安装缆索张力-时间历程曲线。功能舱质量设置为500 t，波浪有义波高分别设置为0.5、1.0、2.0 m。

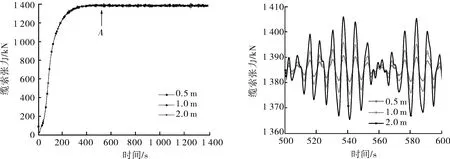
a 全局时历曲线 b A处局部时历曲线

由图9a可知，不同有义波高的张力-时间历程曲线形状与变化趋势基本相同，吊放缆索2解脱后，安装缆索张力均逐渐增大，500 s时趋于平稳并接近最大值。由图9b可知，安装缆索张力曲线的振动波幅随波浪有义波高的增大而增大，缆索张力最大值也随之增大，分别为1.390×106、1.396×106和1.410×106N。

图10为不同有义波高下功能舱xz平面内运动轨迹。

a 全局轨迹 b A处放大轨迹 c B处放大轨迹

由图10a可知，功能舱从坐标点(1 380,0,-51)开始下放，做悬垂运动至指定安装位置。在不同有义波高下，功能舱下放运动轨迹形状基本相同，放大观察发现，有义波高的改变对功能舱悬垂阶段的轨迹影响十分微小。图10b和10c分别为A处和B处的局部放大图，由图10c可知，在接近安装位置的稳定阶段，在有义波高为2.0 m时功能舱出现振幅约为0.1 m的垂荡，而在有义波高为1.0 m及0.5 m时功能舱的振幅约为0.04 m和0.03 m。造成这一现象的原因是由于波浪影响安装船垂荡并通过缆索导致功能舱的垂荡。随着有义波高的增大，功能舱在稳定阶段的垂荡会更加剧烈。

图11为不同有义波高下功能舱纵摇-时间历程曲线。

由图11a可知，在释放时功能舱获得一个较大的角加速度，并且在短时间内倾斜至最大值，有义波高的改变对功能舱纵摇-时间历程曲线的形状及整体趋势影响不大。由图11b可知，在不同有义波高下纵摇最大绝对值均为14.40°，且在下放初期有义波高的改变对功能舱纵摇的影响不大。由图11c可知，在下放进行到中后期至稳定阶段，随着有义波高的增大，功能舱纵摇的振幅随之增大。

a 全局纵摇时历曲线 b A处局部纵摇时历曲线 c B处局部纵摇时历曲线

图12为不同质量的功能舱悬垂下放缆索张力-时间历程曲线，波浪有义波高为1 m。

图12 功能舱质量对缆索张力-时间历程曲线的影响

由图12可知，释放后安装缆索张力均逐渐增大，500 s时接近最大值。功能舱质量对安装缆索的张力影响较大，安装缆张力随功能舱质量的增大而增大，缆索最大张力值为1.200×106、1.397×106、1.495×106和1.593×106N，分别对应功能舱质量480、500、510和520 t。功能舱质量较大时，在悬垂阶段安装缆索张力-时间历程曲线更加陡峭，说明张力变化更加剧烈。以缆索极限断裂载荷(如表3)除以计算最大张力，得出缆索安全系数分别为2.48、2.12、2.00和1.86。

根据2008年公布的API-RP-2SK标准[26]，悬垂下放缆索最低安全系数取2.0。由此可知，在本文模型中功能舱的可下放最大参考质量为510 t，若下放质量更大的功能舱及其他设备，应当增加缆索强度。

图13为不同质量的功能舱悬垂下放轨迹。由图13可知，功能舱质量的增加对其下放整体轨迹形状影响不大。但是，由于质量的增加使得缆索张力增大，导致了较大质量功能舱的轨迹更靠外侧。

图14为不同质量的功能舱悬垂下放过程纵摇-时间历程曲线。由图14可知，功能舱纵摇最大值随其质量的增大而增大，其最大绝对值为13.37、14.40、14.89和15.35°，分别对应功能舱质量480、500、510和520 t。

图13 功能舱质量对其下放轨迹影响

图14 功能舱质量对其纵摇-时间历程曲线的影响

图15为不同重心高度的功能舱悬垂下放缆索张力-时间历程曲线，波浪有义波高为1 m，功能舱质量为500 t。

由图15可知，功能舱重心变化对安装缆张力的影响不大，其最大值均为1.397×106N。

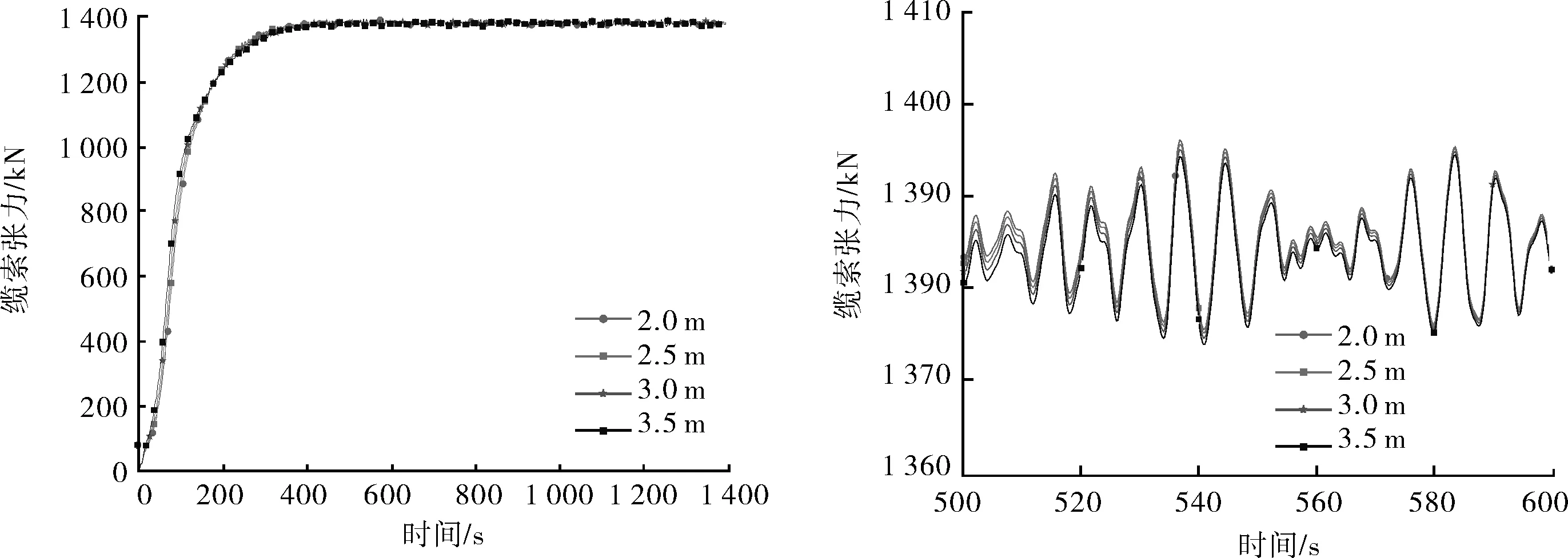
a 全局时历曲线 b 局部时历曲线

图16为不同重心高度的功能舱悬垂下放轨迹。

图16 功能舱重心高度对其下放轨迹影响

由图16可知，功能舱重心变高对其下放整体轨迹形状影响不大，在悬垂阶段重心更高的功能舱轨迹曲线更靠外侧。随着下放的进行，轨迹曲线趋于相似，不同功能舱重心高度对其下放中期及稳定阶段的轨迹影响不大。

图17为不同重心高度的功能舱悬垂下放过程纵摇-时间历程曲线。

由图17可，知功能舱纵摇最大值随其重心高度的增高而增大且影响较大，纵摇最大绝对值为14.40、16.25、19.33和26.02°，分别对应功能舱重心高度2.0、2.5、3.0和3.5 m。因功能舱外形为竖直圆柱形状，重心的改变对其运动纵摇影响较大。当功能舱内设备无法承受较大纵摇角时，应改变其设计形状尺寸，或添加其他外部阻尼来缓冲纵摇运动。

图17 功能舱重心高度对其纵摇-时间历程曲线的影响

4 结语

本文基于ANSYS-AWQA软件建立船-缆-功能舱多体模型，根据DNV-RP-C205规范，设立模拟海况数据作为安装环境条件。通过与文献[22]数据进行对比，验证了模型的有效性。在此基础上研究了不同的波浪有义波高、功能舱质量及功能舱重心高度对安装缆索张力、功能舱下放轨迹及纵摇的影响。

1) 波浪有义波高。改变波浪有义波高，对缆索张力的变化趋势影响不大，对缆索张力-时间历程曲线的振动波幅影响较大。振动波幅随有义波高的增大而增大，缆索张力最大值也随之增大。波浪有义波高的改变对功能舱轨迹及纵摇时影响不大。在稳定阶段，功能舱垂荡及纵摇振幅随波浪有义波高的增大而增大。

2) 功能舱质量。缆索张力随功能舱质量的增大而增大。功能舱质量较大时，在悬垂阶段安装缆张力-时间历程曲线更加陡峭，说明张力变化更加剧烈。功能舱质量的改变对其下放轨迹的整体形状影响不大，但由于缆索张力的增大，使得功能舱下放轨迹随其质量的增大而更靠外侧。在释放后不久，功能舱到达纵摇最大值，最大绝对值随功能舱质量的增加而增大。

3) 功能舱重心高度。改变功能舱重心高度，对安装缆索张力的影响不大。在悬垂阶段，功能舱重心高度会影响功能舱下放轨迹，功能舱重心越高，轨迹越靠外侧。功能舱重心高度的改变对其纵摇影响较大，其最大值均出现在释放后不久的悬垂阶段初期，重心越高，纵摇最大绝对值越大。

在进行功能舱悬垂安装作业时，如果下放质量更大的功能舱及其他设备，应当增加缆索强度；如果功能舱内设备对纵摇稳定性要求较高，则需要改变功能舱尺寸形状、添加外部配重，或增加阻尼来保证其稳定性。