首届全国高中数学联赛平面几何题的两次演变

江苏省苏州市吴江经济技术开发区实验初级中学 (215000) 赵 渊

1979年首届全国高中数学联赛二试的题六是：

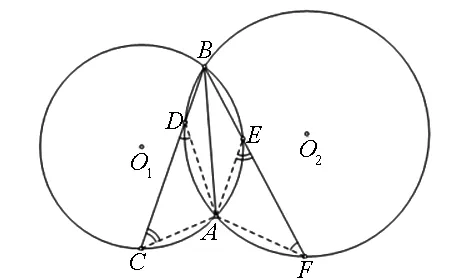
图1

原题如图1，⊙O1与⊙O2相交于点A、B，⊙O1的弦BC交⊙O2于点D，⊙O2的弦BF交⊙O1于点E，证明：∠ABC=∠ABF的充分必要条件是CD=EF．

“旧时王谢堂前燕，飞入寻常百姓家．”

这道赛题平平常常，在现在九年级的众多练习册中都能够看到它的身影．

下面，让我们来看看这道赛题是如何与时俱进、重新演化为全国中学生数学冬令营赛题与另一道全国高中数学联赛加试试题的！

将原题中的“弦”(线段)改成“直线”，并改变图1的面貌，立即得到：

图2

命题1 如图2，⊙O1与⊙O2相交于点A、B，过点B的一条直线分别交⊙O1、⊙O2于点C、D，过点B的另一条直线分别交⊙O1、⊙O2于点E、F，证明：∠ABC=∠ABF的充分必要条件是CD=EF．

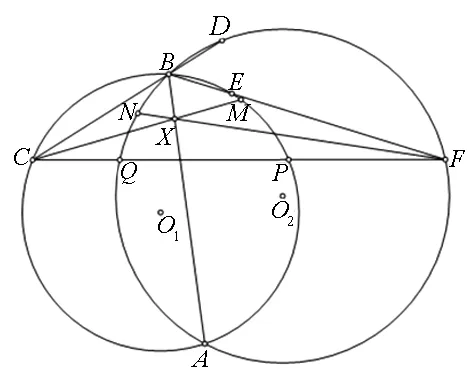
图3

在图1的基础上，连结CF，取CF的中点I，设直线IA与⊙O1、⊙O2分别相交于不同于点A的两点G，H，连结GC、HF(见图4)，则∠CGA=∠ABC=∠ABF=∠AHF．

过点C作CM⊥IA于点M，过点F作FN⊥IA于点N，注意到I是CF的中点，即知ΔCMI≌ΔFNI，故CM=FN，IM=IN，于是ΔGCM≌ΔHFN，从而知GM=HN，即GH+HM=HM+MN，故GH=MN=2IM．

令GH=IA，则IA=MN=2IM，即知CM垂直平分IA，故CA=CI，于是∠CAI=∠CIA，∠GAC=∠HIF，注意到GH=IA，知GA=HI，于是ΔGAC≌ΔHIF．再注意到I是CF的中点，知CF=2CI=2CA．

至此，2019年全国高中数学联赛加试试题(A卷)一水到渠成：

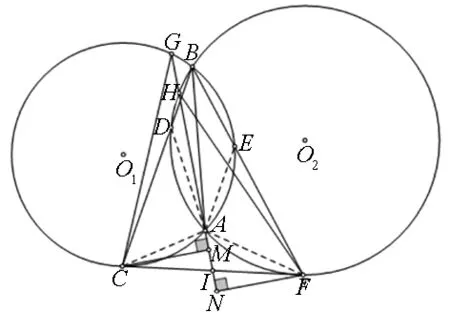
图4

命题4 如图4，在锐角ΔBCF中，I是CF边的中点．点A在ΔBCF内，使得BA平分∠CBF．直线IA与ΔBCA，ΔBFA的外接圆分别相交于不同于点A的两点G，H，证明：若GH=IA，则CF=2CA．