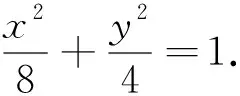活跃于数学高考中的帕斯卡六边形定理*

浙江省绍兴鲁迅中学 (312000) 虞关寿

考题呈现

图1

(1)求证：MN⊥AB；

(2)若弦PQ过椭圆的右焦点F2，求直线MN的方程.

图2

题2 (2014江西高考题)如图2，已知抛物线C:x2=4y，过点M(0,2)任作一直线与C相交于A,B两点，过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).

(1)证明：动点D在定直线上；

(2)作C的任意一条切线l(不含x轴)，与直线y=2相交于点N1，与(1)中的定直线相交于点N2，证明：|MN2|2-|MN1|2为定值，并求此定值.

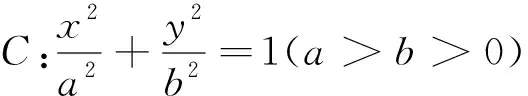
(1)求椭圆C的方程；

(2)动直线y=kx+4与该椭圆交于不同两点M,N，求证：直线BM与直线AN的交点G在定直线上.

这三个考题取之不同的水平考试，但有个共同的特点，就是先用“帕斯卡六边形定理”作预判，得到所要得到的结果，然而有意识地消去一些参量，朝既定的方向进行变形与运算，由于目标已明确，所以我们在解决问题时，不会感到无所适从.从近年的各省市的高考题和数学竞赛题及自主招生题来看，能充分感悟到这类问题都是用“帕斯卡六边形定理”来设计和编拟的，可见“帕斯卡六边形定理”独特的运用价值.

一、帕斯卡六边形定理及证明

帕斯卡六边形定理：如果圆锥曲线的内接六边形的三双对边所在的直线分别相交，那么这三交点共线.

定理的证明通常是先证明圆锥曲线是圆的情形，然后利用“投影、仿映(相似变换)”或运用复平面的旋转变换和平移变换，可证明定理对椭圆、双曲线、抛物线仍然正确.

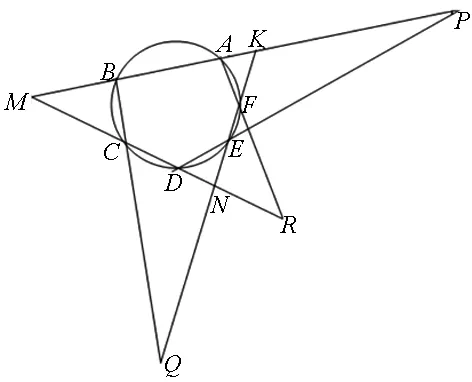
图3

我们把这其中的三交点所在的直线称为帕斯卡直线.

为了使此定理更具完备性，作这样的规定：两条平行直线相交于“无穷远点”，而且平面内的无穷远点在平面内的任意一条直线上.

近年来一些命题专家青睐于以帕斯卡六边形定理为题源，把其一般情形演变到具体、特殊、极端、退化等情形，结合圆锥曲线中的极点与极线理论编制出竞赛题、高考题及自主招生题.

二、帕斯卡六边形定理的特殊化与拓展

1.帕斯卡六边形定理特殊化

把圆锥曲线内接六边形中相邻的两个顶点合成一个点，则可得下列三个推论(以椭圆为例)：

(1)椭圆内接五边形ABCDE,过点A的切线与直线CD相交于点P，直线DE与直线AB相交于点Q，直线BC与直线AE相交于点R，则P,Q,R三点共线；

(2)椭圆内接四边形ABCD，直线AD与直线BC相交于点P，直线AB与直线CD相交于点Q，过点A的切线与过点C的切线相交于点R，则P,Q,R三点共线；

(3)椭圆内接三角形ABC，过点A切线与直线BC相交于点P，过点B的切线与直线AC相交于点Q，过点C的切线与直线AB相交于点R，则P,Q,R三点共线.

2.帕斯卡六边形定理拓展处理

(1)上述所给的内接六边形，我们一般认为它是凸六边形，可验证对凹六边形也是成立的，同样对凹五边形、凹四边形也是成立的；

(2)当一个多边形有一对对边平行时，作这样的规定：两条平行直线相交于“无穷远点”，而且平面内的无穷远点在平面内的任意一条直线上.

三、帕斯卡六边形定理及推论的应用

1.题1分析与解答：

分析：题目中的内接凸四边形APBQ可看作凸六边形AP1P2BQ1Q2的退化形式，其中割线P1P2无限趋近于以点P为切点的切线PT，割线Q1Q2无限趋近于以点Q为切点的切线QT，两切线相交于点T.帕斯卡六边形定理知三点M,N,T共线，设弦PQ与长轴(x轴)的交点坐标为(x0,0)，又由极点与极线的关联性得动点T的轨迹是直线x0x=a2.这样就可以推测两个小题的结论.

解：(1)设P(acosα,bsinα),Q(acosβ,

2.题2分析与解答

分析：设想抛物线C:x2=4y的内接凸六边形A1A2PB1B2O的点P是与y轴正方向同向的无穷远点，当两点A1,A2无限趋近于直到重合于A点，两点B1,B2无限趋近于直到重合于B点时，可理解两条直线AP,BP都平行于y轴，设直线A1A2，即点A处的切线与直线B1B2，即点B处的切线，两切线的交点为E，两直线AP,BO交于点G，则由帕斯卡六边形定理和极限思想可推测知三点D,E,G三点共线，再由极限思想和圆锥曲线的极点与极线理论可推知，动点E的轨迹是点M的极线，易知极线方程为y=-2，显然动点D也在这条定直线上.

3.题3分析与解答

图4