悬挂式铝合金整体壁板压杆的稳定性校核方法
吴剑国,章艺超,张平,陈海涛
1 浙江工业大学 土木学院 , 浙江 杭州 310023
2 中国船舶及海洋工程设计研究院,上海 200011
0 引 言
铝合金材料以其强度高、质量轻、耐腐蚀性强、可挤压成型等优点成为了气垫船结构的首选材料。铝合金气垫船的主要结构形式是悬挂式整体壁板结构。悬挂式整体壁板结构是一种新型的气垫船结构形式,其框架是主要受力构件,强度和稳定性对船体结构的安全至关重要。目前我国对于气垫船结构的稳定性校核主要依据《海上高速船入级与建造规范》[1](以下简称《高速船》),该规范仅有轴心受力和平面单向受弯的计算公式。挪威DNV高速船规范[2]规定了柱的轴心受压校核方法;现行建筑结构的《铝合金结构设计规范》[3](以下简称《铝合金》)有受压杆件平面内外校核公式。
国内外一些学者针对气垫船结构问题也进行了研究。Khedmati等[4]对悬挂式、切口式和悬挂切口混合式铝合金板架的稳定性进行了比较;Herrington等[5]分析了悬挂切口混合式铝合金结构在高速船上的应用;张平[6]针对悬挂式铝合金整体板架特点在气垫船上的应用进行了初步的探索;王伟[7]通过有限元和实验对切口式和悬挂式这2种结构形式的铝合金板架稳定性进行了研究;骆海民[8]对气垫船悬挂式骨架结构设计特点进行了分析。
然而,对于悬挂式整体壁板的受压构件适用于哪种校核方法、如何设置防倾肘板、壁板骨材与桁材焊接对桁材稳定性的影响等这些问题的研究尚少。针对上述问题,本文将比较《高速船》和《铝合金》规范,采用非线性有限元方法,计算分析悬挂式铝合金整体壁板的I字形桁材在不同受力和肘板布置情况下的极限承载力,得到其失稳规律,进而提出悬挂式整体壁板的铝合金压杆的校核方法和肘板布置方法。
1 规范比较
本文将仅列出《高速船》和《铝合金》规范的主要符号含义,详细的符号含义、单位等参见文献[1, 3]。
1.1 轴心受压构件


表 1 轴心受压公式比较Table 1 Comparison of axial compression formulas
对于轴心受压构件的屈曲强度,《高速船》给出了骨材的屈曲应力计算公式。其中,理论屈曲应力需通过塑性修正得到临界屈曲应力,再乘以

1.2 偏心受压比较


表 2 偏心受压公式比较Table 2 Comparison of eccentric compression formulas
对于偏心受压构件,《高速船》只有纵骨、加强筋的梁柱屈曲校核公式,而且该公式只是针对平面内的失稳。《铝合金》中有构件稳定性校核公式,分为单向压弯、双向压弯、平面内、平面外4种,所以更为全面。对于这2个规范都具有的平面内校核公式,其公式基本形式相同,但《高速船》系数是根据骨材形式确定,是一个定值,而《铝合金》稳定系数是根据构件长细比确定,等效弯矩系数是根据构件的受力情况确定。
2 轴心受压构件的稳定性
图1所示为一典型的悬挂式结构图,整体壁板悬挂在桁材上,每个骨材设置一个肋板,骨材面板与桁材焊接连接。但是,当设置了肋板且翼缘宽度小于50 mm时,则可不焊。
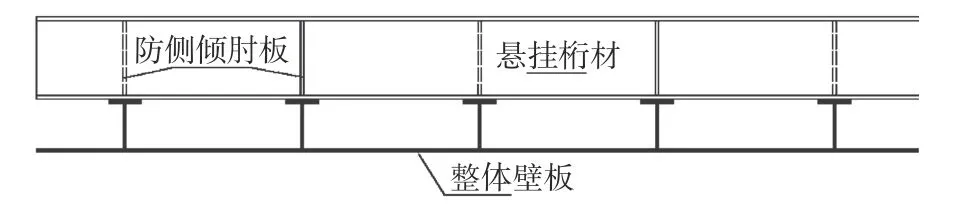
图 1 悬挂式结构图Fig. 1 Schematic diagram of suspended structure
本文针对一根两端简支的悬挂式铝合金桁材建立了有限元模型。其中:桁材长2 000 mm,翼缘宽40 mm,厚7 mm,腹板高150 mm,宽5 mm,整体壁板骨材间距为200 mm。铝合金材料的屈服强度f0.2=215 MPa,弹性模量E=70 000 MPa。
在有限元模型的网格划分中, 将腹板沿高度方向划分为12个板单元,翼缘划分为4个板单元,且网格尽量接近正方形。桁材几何缺陷取线性屈曲分析中的一阶模态,缺陷的幅值为桁材长度的1/1 000。应力和应变的关系采用Ramberg-Osgood模型[9],其中n的取值采用Beson[10]在其研究中的取值27。鉴于翟希梅等[11]在铝合金轴心受压杆有限元分析中得出了模拟结果不受端板厚度影响的结论,本文在有限元计算中将悬挂桁材两端分别刚性耦合到工字形截面的形心点上以代替端板作用。桁材一端在其形心点上约束x,y,z方向的位移,如图2所示,另一端约束y,z方向的位移,放开x方向的位移,并施加一个x方向的集中力F。
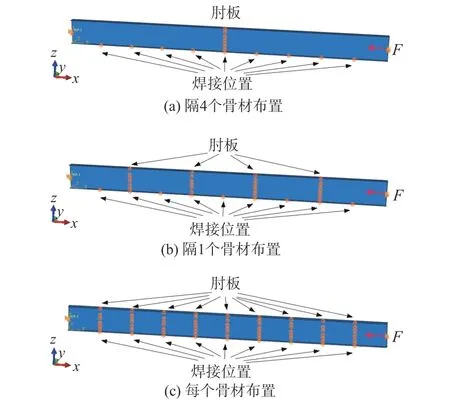
图 2 肘板位置图Fig. 2 Schematic diagram of brackets' position
鉴于整体壁板的抗弯刚度远小于桁材的抗弯刚度,本文偏保守地忽略了整体壁板对桁材z方向的支撑作用。为了研究悬挂桁材防侧倾肘板的布置对桁材稳定性的影响,分别对每个骨材交错布置1个肘板、间隔1个骨材交错布置1个肘板、间隔4个骨材布置1个肘板这3种情况下桁材的稳定性进行分析,模型中肘板作用通过约束肘板处y方向的位移实现。为了研究桁材和骨材焊接情况下桁材稳定性的影响,模型中通过限制焊接部位y方向位移来代替焊接作用。图2所示为肘板设置及焊接位置。
采用上述非线性有限元模型进行非线性分析所得结果与《高速船》和《铝合金》的计算结果列于表3(单位:kN)。为了与有限元结果比较,表3中的规范值未除以安全因子。图3所示为3种有限元模型的轴向应力—应变无量纲化曲线,图中σ为模型的轴向应力;ε为模型的轴向应变;σ0.2为铝合金材料的屈服应力;εy为相应的屈服应变。
在应用《铝合金》规范时,本文通过大量的试算,对于悬挂式桁材,最终确定:当间隔4个骨材布置肘板(如骨材与桁材脱焊(或非焊))时,平面外计算长度取5个骨材的间距,而平面内计算长度取整个桁材的长度;如果是焊接,则平面外计算长度取5个骨材间距的一半;当间隔1个骨材和每个骨材布置肘板时,无论脱焊与否,平面外计算长度都取肋板间距,而平面内计算长度都取整个桁材的长度。

表 3 不同肘板布置下的极限承载力Table 3 Ultimate capacity of different bracket arrangements
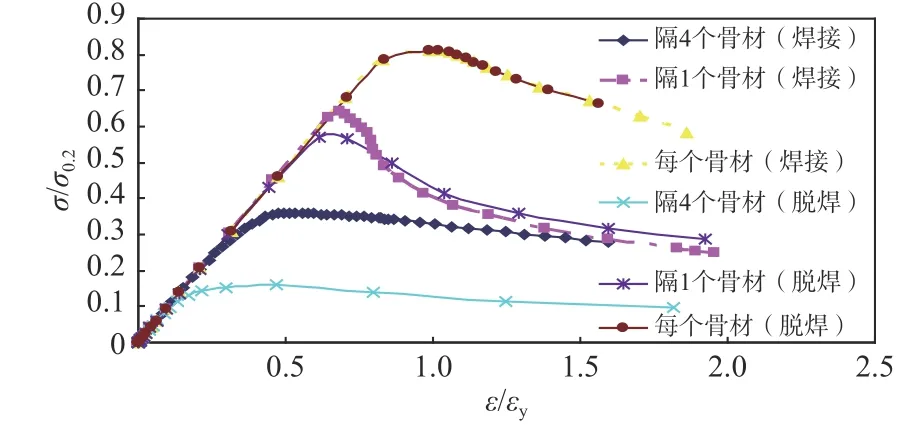
图 3 有限元模型的轴向应力—应变曲线Fig. 3 Axial stress-strain curves of finite element model
因此,由表3和图3可以看出:
1) 当每个骨材设置肘板时,《高速船》和《铝合金》规范值与有限元结果基本一致。随着肘板数目的减少,2个规范和有限元结果的差异越来越明显。这是因为《高速船》是针对设置较密的肘板的情况,并认为不会发生平面外失稳,所以仅列出了平面内失稳的要求,因而不能体现肘板设置的影响。而《铝合金》规范和有限元分析则是取平面内、外极限承载力的较小值。
2) 肘板对于悬挂式桁材稳定性的提高作用很明显,这是因为肘板的布置影响桁材平面外的计算长度,进而影响平面外的长细比。但是当肘板过密时,平面内长细比超过平面外长细比,稳定性就受平面内长细比控制,所以也就无意义了。
3) 当肘板很少时,壁板的骨材与桁材的焊接对稳定性提高有较大的作用,这是因为焊接点限制了桁材平面外的位移,此处的焊接能起到一定的肘板作用。
3 侧向力对轴心受压构件稳定性的影响
鉴于铝合金整体壁板直接悬挂在I字形梁上,其载荷将以侧向力的形式由骨材传递到桁材上。在有限元模型中,通过在桁材与整体壁板骨材焊接处施加一个集中力来模拟。如图4所示,桁材上每隔200 mm施加一个1 kN的集中力。模型的有限元计算结果如表4和图5~图7所示。鉴于每个骨材设置肘板、间隔1个骨材设置肘板时,骨材与桁材焊接与否的影响已很小,图7仅列出了焊接的结果,后续变形图也是如此。

图 4 侧向受压集中力作用位置Fig. 4 Concentration force positions of member subjected to lateral compression

表 4 侧向力作用下压杆的极限载荷与利用系数Table 4 Ultimate loads and utilization factors of pressure bars subjected to lateral force

图 5 每隔4个骨材设肘板模型的变形图Fig. 5 The deformation diagrams of every four frames with a bracket

图 6 不同间距骨材设置肘板时的变形图Fig. 6 The deformation diagrams of bracket-stiffened frame with different spacings
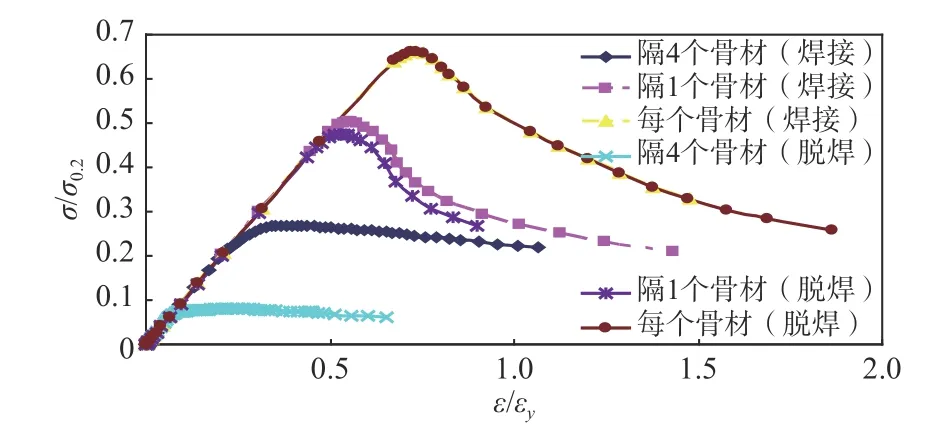
图 7 侧向力受压构件无量纲应力—应变曲线Fig. 7 Dimensionless stress-strain curves of memeber subjected to lateral force
将有限元的极限值作为载荷代入《铝合金》和《高速船》压弯构件的稳定性校核公式。如果表2所示公式左边值(以下称利用系数)等于1,这说明规范给出的极限承载力与有限元结果一致;如利用系数小于1,说明有限元结果小于规范的极限承载力;如利用系数大于1,说明有限元结果大于规范的极限承载力。
从表4和图5~图7可以看出:
1) 对于每个骨材设置肘板的模型,其桁材将发生平面内失稳,《高速船》的极限承载力最小,偏保守,《铝合金》的平面内稳定公式值次之;对于间隔1个骨材设置肘板的模型,《高速船》的极限承载力还是最小,有限元结果与《铝合金》平面内的稳定公式值基本相同;对于间隔4个骨材设置肘板,发生平面外失稳,《高速船》的极限承载力明显偏大。
2) 骨材与桁材的焊接有利于提高平面外的稳定性,尤其是当肘板设置较少时,效果明显。
4 单向偏心受压构件的稳定性
在桁材的上翼缘中点处施加压力,偏心受压点的位置如图8所示,耦合关系与第3节轴心受力情况相同。模型的有限元计算结果如表5和图 9~图 11所示。

图 8 单向偏心受压构件集中力作用位置Fig. 8 Concentrated force positions of member subjected to uniaxial eccentric compression
从表5和图9~图11看出:
1) 对于每个骨材设置肘板的桁材将发生平面内失稳,《高速船》的利用系数为1.56,这说明该规范给出的极限承载力远大于有限元结果,其偏于保守;综合《铝合金》的平面内、外稳定公式的结果,显示出与有限元结果较吻合。

表 5 单向偏心受压构件的极限载荷与利用系数Table 5 Ultimate load and utilization factor of uniaxial eccentric compression members

图 9 间隔4个骨材设肘板模型的变形图Fig. 9 The deformation diagram of every four frames with a bracket

图 10 每隔1个骨材和每个骨材设肘板的变形图Fig. 10 The deformation diagram of every other frame and every one frame with a bracket

图 11 单向偏心受压构件无量纲应力—应变曲线Fig. 11 Dimensionless stress-strain curves of memebers subjected to uniaxial eccentric compression
2) 对于间隔1个骨材设置肘板的桁材,《高速船》的利用系数为1.24,利用系数比《钢结构》和有限元结果大20%,这说明其极限承载力偏小。
3) 对于间隔4个骨材设置肘板,《高速船》的利用系数为0.75,这说明规范给出的极限承载力明显大于限元结果,即该规范不适用于肘板设置太少的情况。综合《铝合金》的平面内、外稳定公式的结果,其与有限元结果较吻合。
4) 骨材与桁材的焊接有利于提高平面外的稳定性,平面外计算长度按照第3节的取值也是合适的。
5 双向偏心受压构件的稳定性
模型上偏心受压点位于上翼缘边上,如图12所示。模型的有限元计算结果如表 6 和图13~图 15所示。
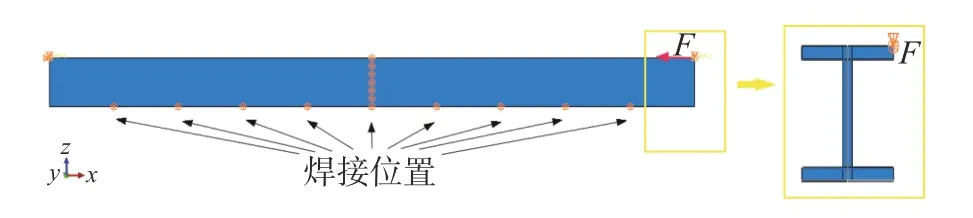
图 12 双向偏心受压构件集中力作用位置Fig. 12 Concentrated force positions of members subjected to biaxial eccentric compression
同样,从表6和图13~图15可以看出:
1) 当间隔4个骨材布置肘板时,双向偏心压弯构件的极限承载力明显较小;当间隔1个骨材布置1道肘板时,极限承载力提高了1倍;当在每个骨材位置布置肘板时,极限承载力最高,与间隔1个骨材设置相比,极限承载力提高了25%。
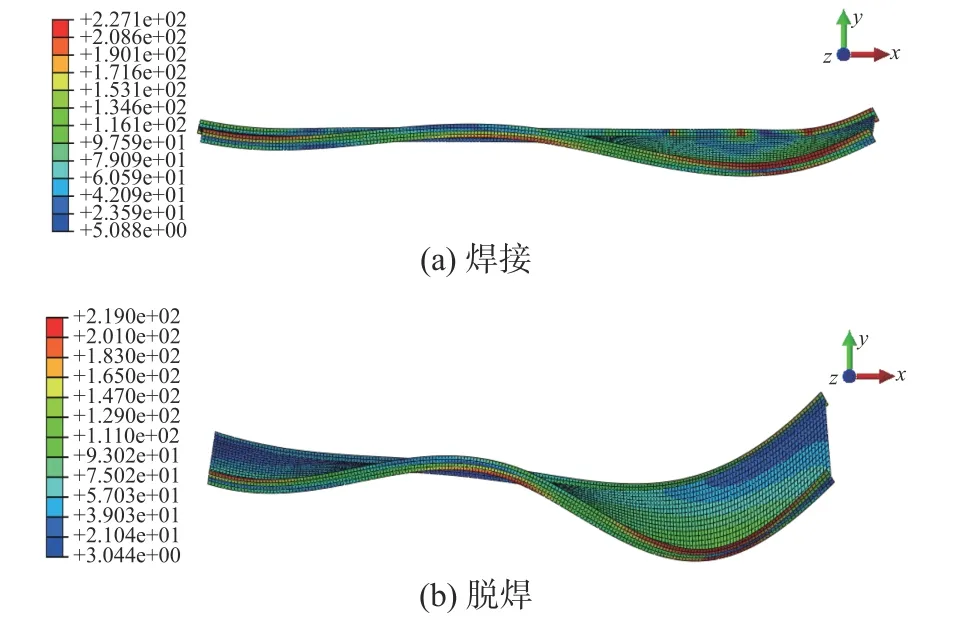
图 13 间隔4个骨材设肘板模型变形图Fig. 13 The deformation diagram of every four frames with a bracket

图 14 每隔1个骨材和每个骨材设肘板时的变形Fig. 14 The deformation diagram of every other frame and every one frame with a bracket

图 15 双向偏心受压构件无量纲应力—应变曲线Fig. 15 Dimensionless stress-strain curves of memebers subjected to biaxial eccentric compression

表 6 双向偏心受压构件的极限载荷与利用系数Table 6 Ultimate loads and utilization factors of biaxial eccentric compression members
2) 《铝合金》对于双向压弯情况下,当肘板设置较多时,校核公式偏于保守。
6 结 论
尽管本文仅是对简支的受压构件进行有限元分析,按照稳定性理论,这些结论也同样适用于像两端固支的压杆,在应用规范校核时只需注意平面内压杆计算长度的固定系数取值。通过将有限元的计算值与本文所述规范的计算值进行比较,得出以下结论:
1) 肘板能显著提高悬挂式铝合金整体壁板压杆的稳定性,但设置过密意义不大。一般情况下,每个骨材位置或间隔1个骨材设置肘板较为合适。
2) 当肘板设置较密时,可采用《高速船》规范进行轴心、偏心的铝合金桁材的稳定性校核;当肘板设置较少时,比如间隔4个骨材设置一个肘板,可采用《铝合金》规范校核压杆平面外的稳定性,此时,应考虑壁板骨材与焊材的焊接作用,平面外计算长度宜取间隔4个骨材设置1个肘板时计算长度的一半。
3) 对双向压弯桁材的稳定性,可采用《铝合金》规范进行校核。

