非等间距随机振荡序列水质参数灰色预测模型研究

廉宇峰，孙宏亮，李丙林，韩丹丹，唐重和，董 冰，刘 格

（1.长春工业大学 电气与电子工程学院，长春 130012；2.长春市市政工程设计研究院，长春130000；3.吉林省计量科学研究院，长春 130103；4.西门子工厂自动化工程有限公司，长春130012；5.江铃汽车股份有限公司，南昌 330001）

0 引言

随着经济的发展和城市化进程的加快，水污染问题变得越来越严重。水质的发展趋势对水污染的控制和防治至关重要。水质监测与预测是水环境管理中最重要的技术。水质可以通过在线检测仪器对电导率、pH、氧化还原电位、浊度、温度等水质参数进行监测与分析［1，2］。虽然水质参数可以由传感器等相关检测仪器直接测量，但由于技术、物理和经济原因，这些传感器不是任何地方都可以安装的。在没有在线测量设备的条件下，有必要开发和应用水质预测技术。为了间接获取水质参数信息，人们提出了数理统计［3］、灰色系统理论［4］、神经网络模型［5］、水质模拟模型［6］等多种水质参数预测方法。在众多预测方法中，灰色系统理论以其利用较少信息来获取系统演化规律的优势被广泛用于水质预测与评估领域中。利用灰色系统理论建立的灰色模型（Grey Model，GM）被广泛应用于水质预测当中。 GM（1，1）模型是由邓聚龙教授提出的最经典的灰色模型之一，除用于水质预测外，还被广泛应用于其他领域［7］。但不同水质指标的变化存在不确定性，尤其是振荡性。GM（1，1）的还原公式是严格单调的齐次指数函数。因此，GM（1，1）很难用于预测不同环境下的水质参数。幸运的是，针对随机振荡序列，一种基于光滑算子的传统随机振荡序列灰色预测模型被提出，即 ROGM（1，1）模型［8］。对于非单调序列，GM（1，1）较差的预测性能可以得到很好的改善。此外，一些水质参数的收集为离线采集。由于技术、物理和经济原因，这些参数并不是实时测量的结果。同时，水质的原始数据往往是非等距序列，大大影响了水质预测模型的预测性能。因此，传统的ROGM（1，1）需要进一步改进，以适应不同环境下的水质参数预测。

1 非等间距随机振荡序列灰色预测模型

信息不完全和不准确是不确定系统的基本特征。由已知信息和未知信息构成的样本较少的不确定系统是灰色系统理论的研究对象。灰色系统理论可以从较少的样本中提取有用信息，实现系统的正确运行，并描述系统的演化规律。用灰色系统理论建立的灰色模型适用于等间距序列，而不适用于非等间距序列。因此，在灰色系统建模之前，需要将非等距序列转化为等间距序列。本文提出了一种非等间距随机振荡序列水质参数预测模型，即NEROGM（1，1），并将其应用于具有离线测量信息的水质预测系统。该灰色预测模型的构建过程如图1所示。

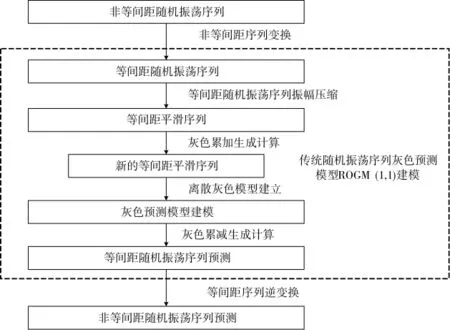
图1 非等间距随机振荡序列水质参数预测模型建模流程图

非等间距随机振荡序列作为水质参数的原始数据，首先将其转化为等间距随机振荡序列。其次，利用振幅压缩将等间距随机振荡序列转化为等间距平滑序列。然后，通过累加计算得到一个新的等间距平滑序列。第四，对模型参数进行估计，并对离散灰色模型DGM（1，1）进行建模。第五，通过模型约简得到等间距随机振荡预测序列。最后，通过等间距序列进行反变换得到非等间距随机振荡预测序列NEROGM（1，1）。

1.1 非等间距变换

设 X（0）＝［x（0）（t1），x（0）（t2），…，x（0）（tn）］为一非等间距序列，则其对应的等间距序列为：

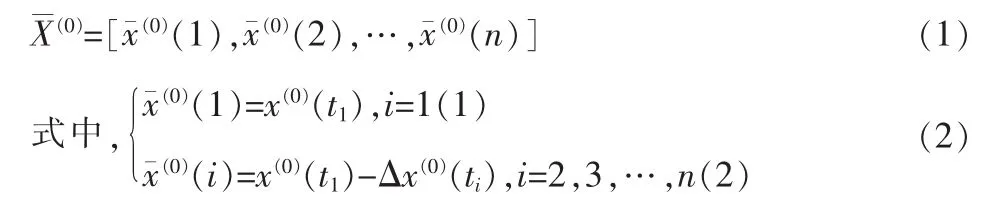
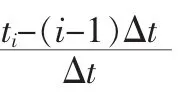
1.2 等间距随机振荡序列灰色预测模型

通过定义2，将等间距随机振荡序列变换成等间距平滑序列。

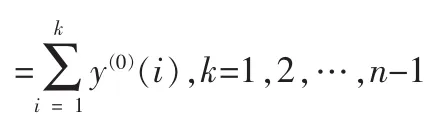
通过定义3，对等间距平滑序列进行累加生成计算，获得新数据序列。

结合 Y（0）和 Y（1），离散灰色模型 DGM （1，1） 可建立如下式形式：

式中，β1和β2为模型参数，其值可通过最小二乘法估计获得；具体公式如下：

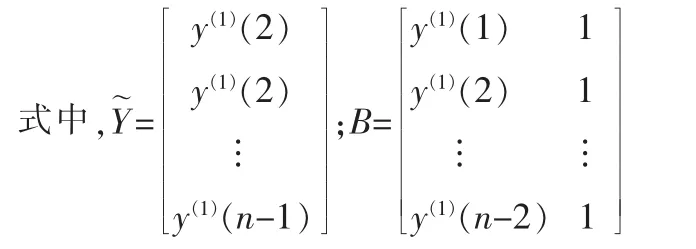
当 y（1）（1）＝y（0）（1）时，离散灰色模型 DGM （1，1） 的还原式如下：

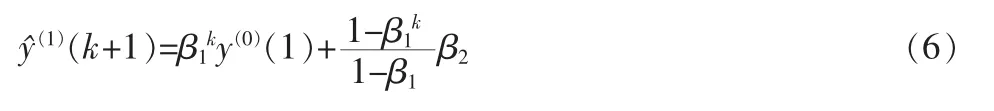
通过定义4，离散灰色模型DGM（1，1）的还原函数表达式为：

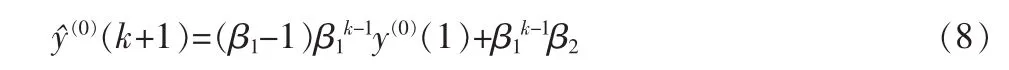
通过定义2，针对等间距随机振荡序列，可获得传统的ROGM （1，1）模型：

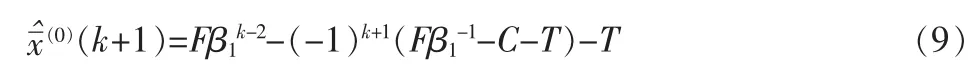
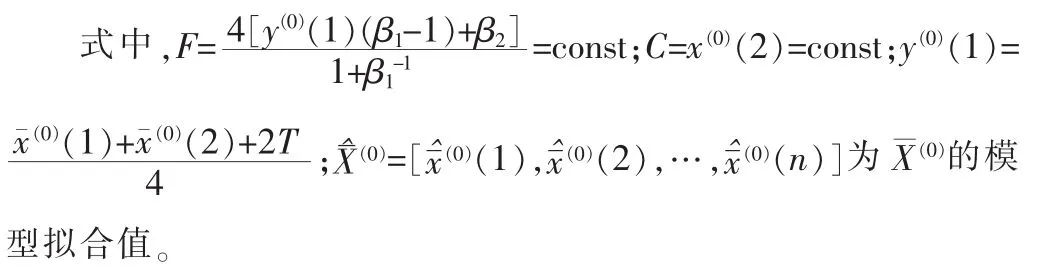
1.3 等间距变换

考虑公式（2），则传 统的 ROGM （1，1）模 型（9）可变换为NEROGM（1，1）：

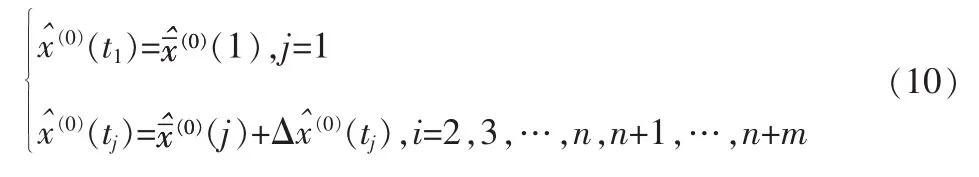
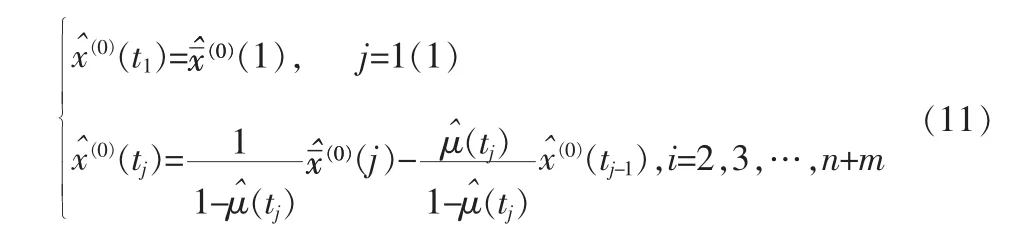
2 水质参数预测系统构建与实验

2.1 水质参数预测系统

基于提出的NEROGM（1，1）模型，设计了一个水质参数预测系统。如图2（1）所示，河中有三个监测点。水质预测系统由监控 PC、S7－200 SMART PLC 和测量传感器组成，如图 2（2）所示。水质参数可以通过测量传感器测量，如pH、溶解氧（DO）、H2S、CH4等。为了方便多点测量，水质参数检测传感器安装在一个离线仪器中。水质参数可通过无线网络传输至S7－200 SMART PLC，并由监控计算机进行监控。由于水质参数是离线检测的，所提出的NEROGM（1，1）可以利用离线测量数据对河流的水质参数进行预测。

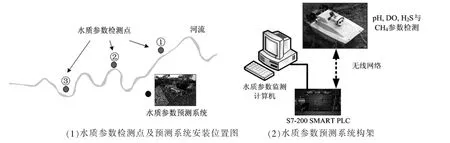
图2 水质参数预测系统

2.2 实验结果与分析

研究工作采用2018年离线仪器测量的pH、溶解氧（DO）等参数，如表1所示。表1显示了5月16日至10月14日的9天数据。通过非等距序列变换，可以得到pH和DO的新的等距序列，如表1所示。如图 3（1）、图 3（2）所示，分别给出 pH和 DO的非等间距序列和等距序列。无论哪个参数，由非等间距序列变换得到的pH和DO等间距序列均可视为随机振荡序列。对于等间距序列，由式（9）可得 ROGM（1，1）的模型值，由式（11）可分别计算NEROGM（1，1）的模型值，如表2所示。原始序列与模型值之间的绝对误差和相对误差都很小。NEROGM（1，1）对pH值的平均相对误差在1%～5%之间，准确度接近1级。NEROGM（1，1）对DO的平均相对误差小于1%，精度等级为1级。这些数据表明，所提出的NEROGM（1，1）在水质拟合中是有效和可行的。如图 3（3）、图 3（4）所示，NEROGM（1，1）的拟合值可以很好地逼近原始序列，而NEROGM（1，1）的实际值与预测值之间的绝对误差和相对误差相对较大。NEROGM（1，1）对pH和DO的预测值分别列于表3。NEROGM（1，1）对pH和DO的平均相对误差都在5%到10%之间，准确度接近2级。利用原序列拟合原序列，对已知的原序列拟合效果较好。然而，使用原始序列预测数据，会有一些误差。虽然预测过程中存在一些误差，但NEROGM（1，1）的平均相对误差均小于20%，可以作为预测模型对水质参数进行预测。这些数据表明，所提出的NEROGM（1，1）在水质预测中也是有效和可行的。

表1 原始非等间距序列与变换后的等间距序列

表2 NEROGM （1，1）模型拟合值

续表2

表3 NEROGM （1，1）模型预测值

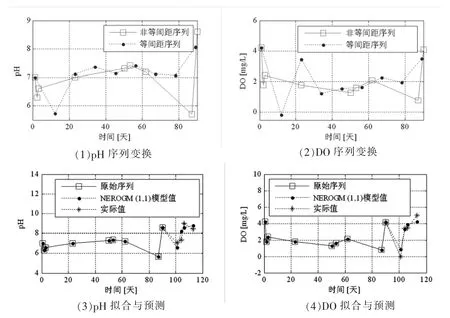
图3 序列变换与NEROG（1，1）模型预测

3 结论

本文提出了一种基于非等间距随机振荡序列灰色预测模型的水质参数系统，可以有效地改善预测模型误差大的问题。在无法实现对河流水质的实时监测的条件下，该系统实现了对河流水质参数的预测。所提出的NEROGM（1，1）能够较好地逼近原始序列，对水质参数具有较好的预测效果，对水环境管理具有一定的指导意义。在水质参数预测系统中除了水质预测外，没有给出水质评价方法。因此，需要在该水质预测系统中开发和应用水质

评价的理论方法，使整个系统的功能更加完善。这项工作有待今后进一步研究改进。