基于“一线三等角模型”的创新能力综合题设计

张大任

摘要：数学题设计的目的不仅仅在于让学生通过练习巩固课上所学的知识，还为了让学生在分析题目的过程中锻炼思维逻辑，将基础知识转化运用到题目的解析中，增强综合分析能力。因此需要对数学题型进行创新，通过对基础题目的深入研究，设计一些隐藏条件，将题目变式，让学生在解析过程中学会发散思维，对所学知识进行合理的应用。本文在“一线三等角模型”的基础上，从存在的问题、意义和设计策略三个方面对数学创新能力综合题的设计进行相关分析。

关键词：一线三等角模型;创新能力;试题设计

在“一线三等角模型”这一章节，应用到的几何理论有相似性、全等性、勾股定理、余角、补角等。简单的试题包含了明显的解题条件，学生读一遍题目根据已知条件就能轻而易举地解出答案，在解题过程中没有进行思维转变和解法的创新，不利于学生灵活地运用几何知识解决问题。因此，将数学试题进行合理地创新，适当地增加题型难度，减少题目中的明确条件等，对学生学好数学十分有利。

一、数学试题设计存在的问题

1.题目中已知条件过多，题型过于简单

对于“一线三等角模型”的相关试题，题干中的已知条件多，大大降低了题型的难度。比如给出了多个角的度数、线段的比例关系和角与角之间的关系等，使得学生根据条件不用思考就能得出答案，不利于学生综合运用所学的几何知识进行思索和分析，使试题失去了考查意义。

2.求证类型的题目缺少对学生自主探索的训练

一般情况下，几何试题的第一小问都是让求证角与角之间垂直、平分或线段相等的证明题，问题中直接说明了两者的关系，学生只要结合题目中所给的相关信息进行论证即可。这样会让学生一门心思地找各种论据来证明结论，不利于学生自主思考两者之间的关系进行探索证明，而是被动地为结论找证明条件，不利于激发学生对试题产生探索兴趣。

3.缺少对几何图形的动态设计

几何试题的图形大都是固定的，缺少对几何图形的创新设计，比如将图形进行折叠、翻转等变化。固定的几何图形使学生的思维产生局限性，不利于发展学生的思维逻辑和想象能力。学生对动态图形相关试题练习的次数较少，使学生对此类的试题比较陌生，不知从哪里入手，影响学生对“一线三角模型”试题的全面掌握。

二、试题改编创新的意义

1.促进学生合理运用知识

学生学习完“一线三等角模型”的相关知识后，对于几何的基本概念和几种定理有了初步的掌握，通过做题能够再次巩固所学知识。在普通试题的基础上，对题目进行创新改编，将多个知识点综合到一道题上，有利于让学生深度的解读题目要求，结合所学的相关几何知识，分析题目所包含的知识点，从而找到解答的方法。这样能使学生将所有知识点都出现在脑海里，选择与题目相符的知识点进行综合运用，提高知识运用能力。

2.增强学生的思维拓展能力

普通幾何试题的题干中几乎包含了所有的解题条件，对于这种简单题型学生不用刻意地思考就能够轻而易举地解答出来，不利于学生的思维锻炼。将几何试题创新化，减少题目中的显性条件，将条件隐含到图形中，有利于学生自主地分析几何图形，寻找角与角之间的关系，思考潜在的条件，拓展思维。

3.增强学生探索几何知识的兴趣

设计创新能力综合题能够激发学生的兴趣和挑战，学生对简单的题目没有压力，而对于创新型综合题没有十足的把握能够很快做出来。所以对几何试题进行创新改编，融合多个方面的知识，设计一定的难度，激发学生战胜难题的斗志，从而能使学生更加喜欢研究几何知识和试题，有助于增强学生对数学的兴趣。

三、创新能力综合题的设计策略

1.减少题目中的已知条件数量，合理地增加难度

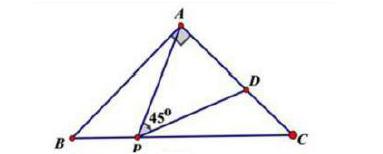
在“一线三等角模型”试题的创新方面，应注重对题目的设计技巧，减少题干中的已知条件，将一些条件隐藏在图形中，让学生通过读题干挖掘隐含条件，攻克试题的难度。比如给出一个角的度数和线段比例关系，学生可以根据全等、互补等隐含条件求出另一个角的度数。还可以让学生通过添加辅助线进行解答，这样适当的增加题型难度，能够锻炼学生的探索能力，收获战胜难题的满足感。例如：等腰直角ABC的直角边AB的长为4，P为斜边BC上一点，且BP=2，D为AC上一点，且∠APD=45°，试求CD的长。

题目中给出的明确条件有三个，学生可以通过分析确定此题属于一线三等角的类型，通过相关知识的运用，可证明三角形相似进而求CD的长度。如下解：

因为△ABC是等腰直角三角形，所以∠B=∠C=45°， BC=√2AB=4√2，∠B+∠BAP+∠BPA=∠CPD+∠APD+∠BPA=180°，∠APD=45°，∠B=∠CPD ，所以△APB∽△PDC，所以CD：BP=PC：AB即 CD：2=（4√2 -2）：4，所以CD=2√2 -1

2.问题设定时避免让学生直接论证结论

在几何试题的分问题设计中，尽量不要让学生直接求证某个结论，比如∠A⊥∠B或者AM平分∠AOB等，这样直接给出结论影响学生对于图形更好地探索与理解。在设计问题时应该让学生猜想两者之间的关系并进行论证。这样能够让学生的思维进行发散，自己探索两者的关系，充分运用题干中所给的条件进行验证，检验猜想是否正确。

3.对几何图形进行动态设计

“一线三等角模型”的相关试题中，所分析的几何图形大都是固定的。为了增强学生的学习能力，应该增加图形翻转、对折等条件，促进想象力的发展。动态变化的题型比较新颖，同时也增加了一定的难度，学生多练习这类试题，有助于数学学习水平的提高。

结束语

学生学习“一线三等角模型”这一章节，在掌握基础知识的同时，进行大量的试题训练十分重要。试题的质量影响到学生的学习效果，因此要加强对数学试题的研究，在传统试题的基础上进行创新改编，注重对几何图形的转化与设计，从而增强对数学的学习效果。

参考文献：

[1]王振鑫，张璇.“多变”的一线三等角——一节变式教学课的教学策略研究[J].中学数学，2019（18）：46-47+49.

[2]汤建武.透视复合问题，提炼数学模型——“一线三等角”模型的提炼与剖析[J].数学教学通讯，2019（23）：86-88.