一类分数阶混合型差分与和分方程任意初值问题解的存在唯一性

张晓锐，王良龙

(安徽大学 数学科学学院，合肥 230039)

0 引言

1695年，数学家Leibniz和 L’Hospitals进行了有意义的交流，探讨是否可以把整数阶微分方程推广到分数阶分数阶微分方程，甚至是无理数微分方程[1]。之后，出于理论研究和实际应用的需要，分数阶微分方程的理论和应用获得了极大发展，其研究成果层出不穷[2，3]。分数阶微分方程研究中，Riemann-Liouville型分数阶微分方程更为活跃，并在控制论、生物模型、电路理论等学科领域获得广泛应用[4]。

众所周知，对一般的分数阶微分方程也很难获得其解的解析表达式或精确表示。为了寻找解的精确表达，人们经常将分数阶微分方程进行离散化，获得相应的分数阶差分方程。相对于分数阶微分方程来说，分数阶差分方程之发展相对较晚，但出于理论研究和应用需求，近年来分数阶差分方程的理论和应用获得极大发展，引起数学研究者和应用工作者的广泛关注[5]。事实上，分数阶差分、分数阶和分、分数阶差分方程的理论研究具有很大的挑战性，并在材料科学、医药科学、生态数学模型的研究上具有重要应用[6-7]。

2016年，曹玉童[8]研究了一类Riemann-Loiuville型分数阶差分方程的初值问题

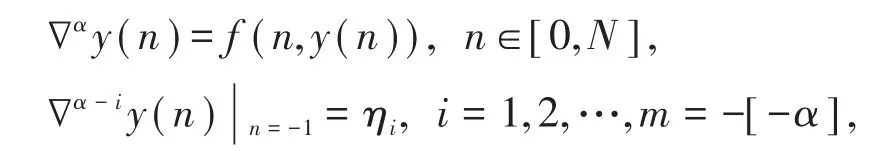
通过构造Volterra和分方程，再利用离散分数阶Gronwall不等式和离散Mittag-Leffler函数的性质，在合适的条件下获得这个方程解对初值的连续依赖性。

2017年，何超[9]研究了下列Caputo型分数阶差分方程的初值问题

其中0＜α＜1 ,f: [0,b]N0×R→R局部有界。通过给定的初值条件，构造与初值问题解等价的Volterra和分方程，再利用迭代法和分数阶离散Gronwall不等式，证明了该初值问题解的存在唯一性和解对初值的连续依赖性。

本文研究如下一类Riemann-Liouville型混合分数阶差分与和分方程的初值问题

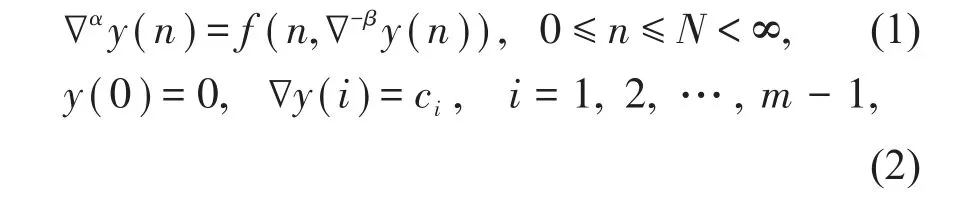
其中m=-[-α]为非负数，0＜β＜1 ,m-1＜α+β＜m,f: [α-m,α+b]Nα-m×R→R是连续函数，f(0,0)=0 .通过构造与初值问题解等价的Volterra和分方程，结合使用Banach压缩映射原理，得到初值问题解的存在唯一性；另外，还通过构造离散Mittag-Leffler函数，结合运用离散分数阶Gronwall不等式，证明了上述初值问题解的存在唯一性。

1 预备知识

本文沿用程金发[5]的分数阶差分方程理论的记号与定义。设a,b为整数，且a＜b，记Na={a,a+1,…}，Na,b={a,a+1,…,b} . 离 散 函 数x(n)和y(n)的卷积定义为：

设n是一个整数，x是实数，记

定义1 假设k∈N+为非负整数，定义x(n)的一阶向后差分为

∇x(n)=x(n)-x(n-1)，

称 ∇kx(n)=∇∇k-1x(n)为x(n)的k阶向后差分，其中k∈N+.

定义2 定义x(n)的一阶向后和分为

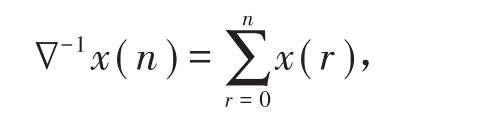
称 ∇-kx(n)= ∇-1∇-(k-1)x(n)为x(n)的k阶阶向后和分向后和分，其中k∈N+.

定义3 假设v＞0,离散函数x(n)的v阶和分定义为

离散函数x(n)的v阶Riemann-Liouville型差分定义为 ∇vx(n)= ∇m∇-(m-v)x(n) ,其中m=-[-v] .

引理 1 假设p＞0,m=-[-p]，则x(n)的p阶和分有下列计算公式

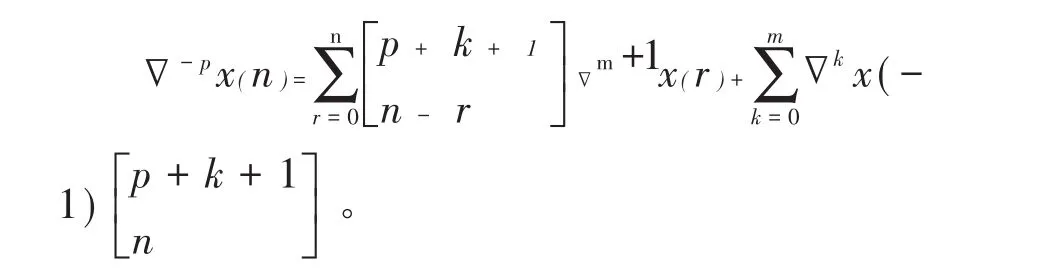
引理 2 假设α,β∈R+,λ∈C,记 Mittag-Leffler 函 数 为，则当是收敛的。

引理3 假设v＞0,u为实数，则有

引理4 (分数阶Gronwall不等式)假设β＞0,u(n)和a(n)为非负数列，0≤b＜1。如果u(n)≤a(n)+b∇-βu(n)，那么特别地 ，若a(n)≡ 0,则u(n)≡ 0.

引理5 (Banach压缩映射定理)设E是Banach空间，映射T:X→X是一个压缩映射，则T在X上有唯一不动点。

2 主要结果

定理1 初值问题(1)(2)的解等价于方程

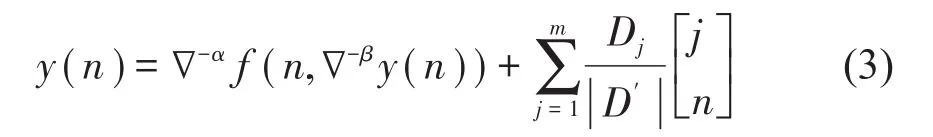
的解，其中Dj为D′的第j列换成列向量C=(c1,c2,…,cm)T所成的行列式，j=1, 2, …,m,

cj，D′见(4)(5)。

证明先证必要性。把D′的第i行加到第(i+1)行(i=1, 2, …,m-1)，此时矩阵D′化为(6)。

根据文[7]知，行列式| |D≠0，从而行列式|D′|≠0，仿照文[7]可证必要性成立。由分数阶差分、分数阶和分的性质，易证(3)的解y(n)满足(1)和(2)。

定理2设函数f满足Lipschitz条件，即存在非负常数L，使得

则(B, ‖·‖ )为一个Banach空间。在B上定义算子T如下

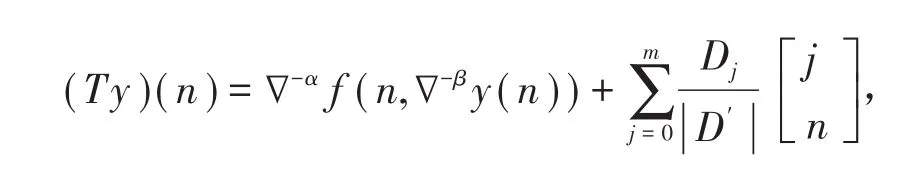
显然，若y∈B为T的不动点，则y为初值问题(1)(2)的解。直接计算可得(7)。

由假设条件可知，T：B→B是压缩映射，又由引理5知，T有唯一不动点y(n)，此y(n)即为初值问题(1)(2)的唯一解。

定理3若初值问题(1)(2)满足以下条件：

(1) |f(n,z1)-f(n,z2) |≤L|z1-z2|, 0 ≤L＜ 1 ；

(2)|f(n,z) |≤A|z|+B,z∈[0,∞) ,其中A和B为非负常数，

则初值问题(1)(2)存在唯一解。

证明先证存在性。构造迭代数列

下证解的唯一性。假设初值(1)(2)存在两个解y1(n)和y2(n)， 则有

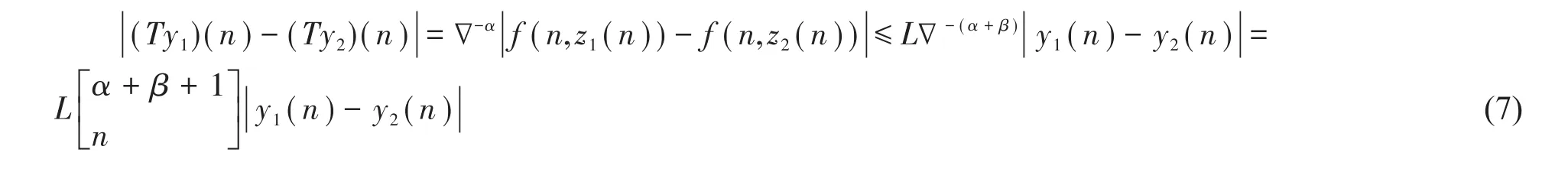
由分数阶离散Gronwall不等式知，y1(n)≡y2(n)，所以解是唯一的。