基于改进TEB算法的阿克曼机器人运动规划系统
郑凯林,韩宝玲,王新达
(北京理工大学机械与车辆学院,北京 100081)
移动机器人的路径规划分为全局路径规划和局部路径规划。全局路径规划负责在全局地图寻找一条从起点到终点无碰撞的路径,但一般不具有实时更新路径动态避障而且满足运动学动力学约束的特点。局部路径规划起到修饰全局路径,动态更新调整路径避开动态障碍物的作用,机器人局部路径规划中常见的算法有动态窗口法[1],在可行的速度采样空间[v,w],模拟在未来时间段机器人可以达到的轨迹集合。设置评价函数评估轨迹的代价,选择代价最小的轨迹对应的速度发送给机器人底盘。该方法适用于全向移动和差速机器人,不适用阿克曼转向几何约束的机器人。广东工业大学徐宝来等提出了适用阿克曼机器人的改进动态窗口法,将线速度角速度采样空间[v,w]替换成线速度虚拟转向角空间[v,α][2],轨迹的优劣受采样的分辨率和评价函数的参数有关,而且控制动作在预测范围内保持不变。人工势场法[3]也是广泛应用在机器人局部路径规划上[4],但是机器人容易陷入障碍物斥力函数和目标点引力函数平衡而造成目标点不可达。燕山大学王洪斌等提出增设虚拟子目标的方法解决局部极小值问题,利用自适应步长调节算法对移动机器人的步长进行了动态优化[5]。改进的人工势场法都是为了机器人避开障碍物脱困,并无对具有非完整约束的阿克曼机器人运动学和动力学的考虑。Rosmann等提出了TEB算法[6],该算法将传统的运动规划问题表述为一个图优化问题,可以适用于完整约束和非完整约束机器人[7],后又针对阿克曼机器人进行了扩充支持[8],由牛顿第二定律可知,加速度反映在加速度运动时受到的力,加加速度则反映这作用力的变化快慢。较大的加加速度将会产生冲击感,例如在电梯升降,汽车、飞机等加速和转弯的过程中。
对于机器人而言,缺少对加加速度的约束,电机输出力矩短时间产生较大范围突变会对阿克曼机器人产生冲击震荡。在此研究基础上,现在多目标优化问题约束上构建加加速度约束,使动力学约束更加完善,并将该算法应用在阿克曼机器人运动规划上,进行了仿真和真实机器人实验。将从阿克曼机器人运动学模型构建、TEB算法模型构建和求解优化改进、导航框架设计、仿真和真实机器人测试等方面进行论述。
1 阿克曼机器人运动模型构建
机器人运动规划需要建立机器人的运动学模型,在世界坐标下对阿克曼机器人构型描述如图1所示。

图1 阿克曼机器人在世界坐标系的构型
世界坐标系为OWXWYW,机器人的基坐标系设置在机器人后轴中心Or上,ICR是阿克曼机器人的瞬时旋转中心,后轴速度为v,机器人的前轮虚拟转向角α,方向角为θ,机器人的转弯半径为R,机器人前后轴轴距为L, 后轮两轮距为2l。其中转弯半径R与轴距和前轮虚拟转向角α有关,不能无限小,需满足:
R=L/tan[α(t)]
(1)
w=v(t)/R
(2)
式中:w为机器人后轴角速度。
阿克曼机器人运动学状态方程建立如下:
(3)
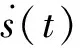
(4)
阿克曼机器人的控制输入量u(t)=[v(t),α(t)]T,虚拟转向角α(t)因为阿克曼转向几何机构[9]存在一个范围。
2 TEB算法模型构建以及改进约束
2.1 TEB轨迹模型构建
TEB将机器人的一系列位姿轨迹模型抽象成带有时间信息的弹性带模型。机器人的第i个位姿状态可以表示为si=[xi,yi,θi],位姿包含位置信息xi、yi和方向角θi。ΔTi是机器人位姿si和si+1的过渡时间间隔。TEB的轨迹序列可以表示为如图2所示。

图2 机器人在世界坐标系下的轨迹序列
机器人在世界坐标系XOY下的位姿序列可以表示为
C={si},i=0,1,…,n;n∈N
(5)
TEB描述的轨迹模型的位姿si到si+1的时间间隔为ΔTi,n个位姿间隔的时间序列为
Δτ={ΔTi},i=0,1,…,n-1
(6)
每个时间间隔表示机器人从一个位姿运动到另一个位姿的时间。TEB轨迹模型包含位姿序列信息和时间间隔序列信息,轨迹信息可以表示为
T:=(C,Δτ)
(7)
TEB算法存在的约束目标如下:
2.2.1 避开障碍物
机器人的轨迹是必须满足避开障碍物[10]。机器人的距离与障碍物的距离为d,机器人与障碍物的允许距离为dmin,障碍物根据环境动态更新,障碍物的位置可以通过激光雷达获取,在代价地图上读取障碍物的位置。对于每个位姿,可能受n个障碍物影响,需要考虑对某个位姿的n个障碍物影响。当障碍物超过机器人与障碍物允许的最小距离时,约束函数的值为0。当机器人与障碍物的距离小于限制的距离,障碍物约束函数才起作用。约束函数如下:
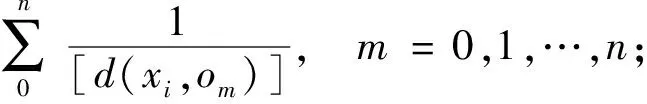
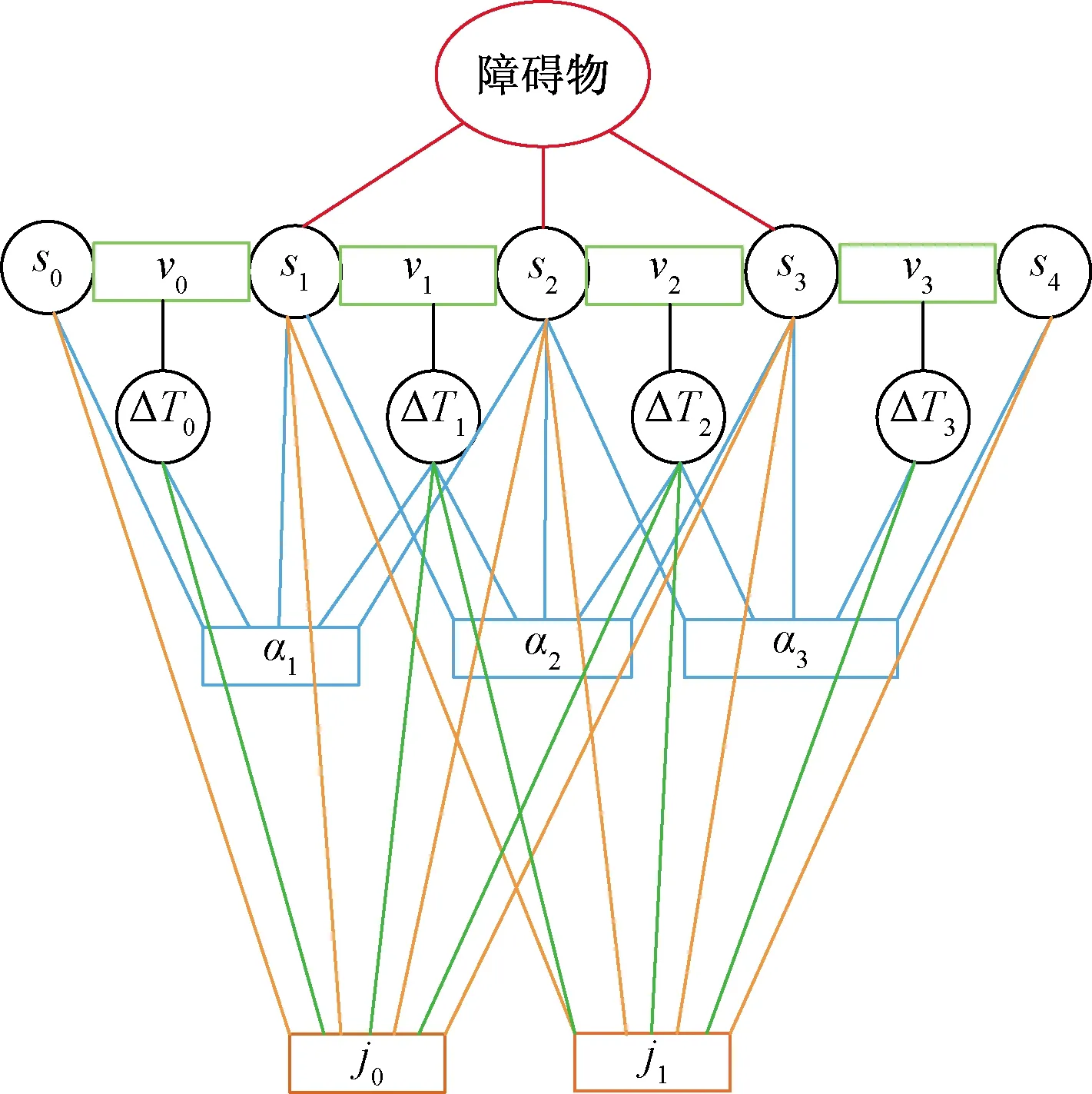
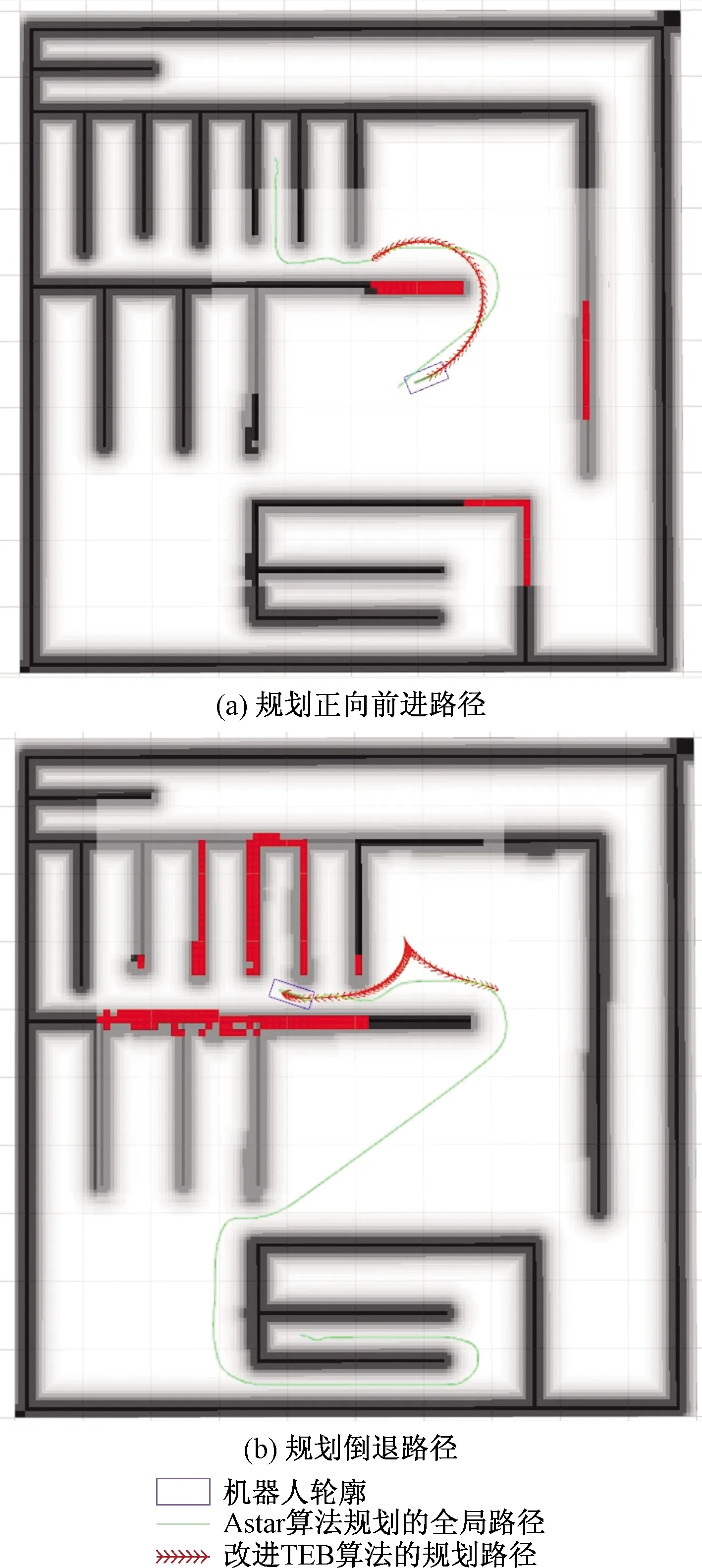
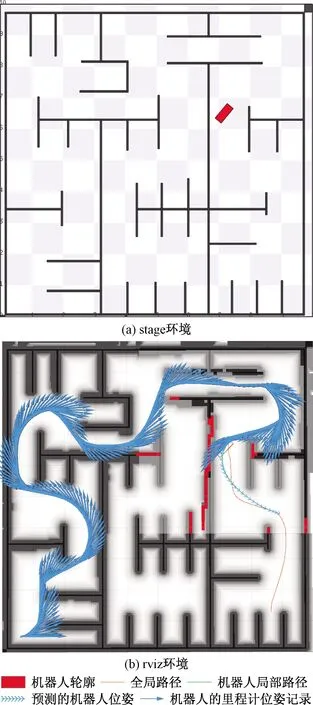
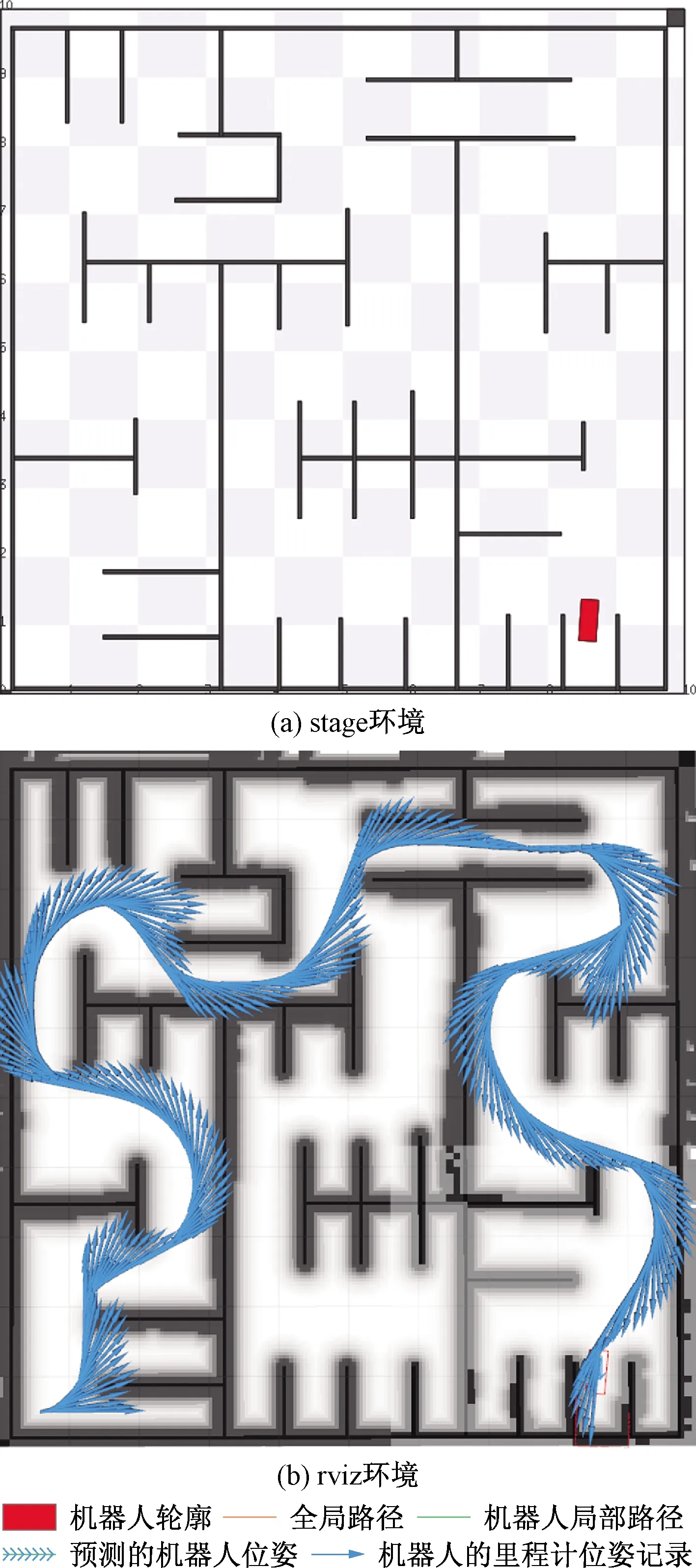
d (8) 2.1.2 速度和加速度约束 机器人速度和加速度的动态约束通过类似的惩罚函数来描述几何约束。平均平移和旋转速度分别根据欧式距离和方向角的改变量计算,在两个连续的位姿xi、xi+1和两个姿势之间的过渡的时间间隔ΔTi[11]。 线速度: (9) 角速度: wi≃(θi+1-θi)/ΔTi (10) 线加速度: ai≃2(vi+1-vi)/(ΔTi+ΔTi+1) (11) 角加速度: αi=2(wi+1-wi)/(ΔTi+ΔTi+1) (12) 2.1.3 非完整运动学约束 非完整约束机器人相邻的两个位姿移动可近似为曲率不变的弧线运动[12]。阿克曼机器人以恒定速率转弯如图3所示。 图3 阿克曼机器人转弯示意图 机器人的位姿状态由si运动到si + 1,机器人做圆周运动,si和si+1都落在曲率不变的圆弧上,其中满足: βi ,i=βi ,i + 1 (13) (14) (15) 式(15)中:θi和θi+1机器人在世界坐标系的方向角,非完整约束的代价函数表示为 (16) 阿克曼机器人的转弯半径必须大于等于最小转弯半径 (17) 2.1.4 最短时间的目标函数约束 最快时间是考虑TEB全局性,因为目标函数需要依赖于所有的参数。是通过最小化所有时间间隔之和的平方要求机器人尽可能快地到达规划的终点。最短时间约束函数可表示为 (18) TEB的核心思想是求解出一系列这样的最优的带有时间间隔的机器人位姿序列。目标函数的大部分位姿是局部的,因为它们仅取决于少数几个连续位姿的数量,而不是整条全局轨迹上的位姿。TEB的局部性导致稀疏系统矩阵的产生,可以使用专用的快速有效的大规模数值优化方法[13]求解。关键思想是通过调整位姿和时间间隔来优化TEB,使用权重求和模型求解多目标优化问题。通过构建多目标优化得到最优的位姿和时间间隔。 (19) T*=argTminf(T) (20) 式中:T*表示优化的TEB结果;γk是函数k的权重系数;f(T)表示各种约束目标函数之和,它是各目标函数乘以权重系数的和。TEB优化问题[式(18)]可以转化为hyper-graph(超图)问题,所谓 的超图是其中一条边的连接节点不受限制。因此,一条边可以连接两个以上的节点。TEB求解问题能够转换成以位姿和时间间隔为节点的超图。节点之间通过给定的目标函数 相连。图4显示了位姿、时间间隔、速度、加速度之间的连接关系。速度约束目标函数需要知道两个位姿欧式距离之差和时间间隔,因此,它形成了一条连接机器人位姿和时间间隔的边。同理,加速度约束函数也是这样。障碍物需要一条边连接到能影响机器人的几个位姿。代表障碍物的椭圆节点是无法优化的。根据位姿,时间间隔、速度、加速度以及障碍物构建出的超图如4所示。 图4 超图 解决具有硬约束的非线性问题在计算代价非常大。因此,提高效率快速在线求解一直是非线性研究的重点。非线性问题转化为近似非线性平方优化问题,当求解器利用问题的稀疏模式时,它通过一阶导数逼近Hessian矩阵,从而有效地解决了该问题。约束作为惩罚项纳入目标函数[8]。 为了求解方程利用LevenbergMarquardt(LM)方法,因为它兼顾鲁棒性和效率。图优化框架g2o[14]实现LM的高效稀疏变量求解方程[式(20)]。 TEB以一定的频率进行重复求解,这个频率高于机器人的响应控制周期。在每个轨迹修正步骤中,TEB算法都会动态添加新的位姿和删除以前的位姿,为了将时空分辨率调整剩余的轨迹长度或规划范围。对于实时更新的障碍物,TEB在优化的那一时刻当作静态障碍物来处理。g2o框架批量优化了TEB轨迹,因此每次迭代都会生成一个新图。在单个机器人控制周期内,每个循环进行多次循环迭代求解。在每个采样周期中,控制输入量u(t)从优化的轨迹中得到。TEB算法流程如下: 1输入全局路径,给定机器人的起始位姿和终点位姿;2截取一段全局路径,获得初始化轨迹(包含机器人位姿和默认时间间隔),构建多目标优化问题;3进入迭代求解循环4 调节修剪局部轨迹长度,维持局部优化的轨迹长度不变,删除机器人走过的固定长度的轨迹;5 更新代价地图中的障碍物信息;6 建立hyper-graph(超图)进行多次迭代求解出最优轨迹列;7 检查轨迹是否可行;8 将式(19)B∗映射到u(t),根据相邻的轨迹点计算出控制量信息包括后轴速度和前轮虚拟转向角;9 到达终点,结束算法; 得到优化的TEB轨迹之后,控制变量速度v和阿克曼机器人的虚拟转角α可以计算出来下发给机器人驱动器。在每次新迭代之前,重新初始化阶段都会检查新的和更改的位姿点。 在机器人的运动过程中,加速度约束能保证速度变化率不会太大。加速度的变化率过大会对机器人造成冲击。增加加加速度约束,将加加速度的变化率限定在一个较小的范围,提高机器人运动的平顺性以及提高电机的寿命,现将加加速度约束添加到超图中,构建新的超图。j0这条边连接到这三个ΔT0、ΔT1、ΔT2这三个时间间隔顶点和s0、s1、s2、s3这四个位姿顶点,j1连接的时间间隔和位姿数量不变,分别往后顺延一个序号,如图4所示: 图5 改进的超图 s0、s1、s2、s3、s4是机器人连续的5个位姿状态,v0、v1、v2、v3是连接上述5个位姿的速度状态(包含线速度和角速度),a0、a1、a2是加速度状态(包含线加速度和角加速度),j0、j1满足的加加速度约束关系如下: 线加加速度可表示为 j0lin=(a1lin-a0lin)/(0.25ΔT0+0.5ΔT1+ 0.25ΔT2) (21) 角加加速度可表示为 j0rot=(a1rot-a0rot)/(0.25ΔT0+0.5ΔT1+ 0.25ΔT2) (22) 在程序实现过程中需要重新给g2o库定义加加速度边作为约束条件和添加加加速度约束。在局部规划起始状态和中间状态以及终点状态中分别应用。 整个运动规划框架的设计基于机器人ROS系统,利用ROS的通信机制进行通信[15]。利用开源的move_base充当决策层提供action通信机制,给定一个全局导航目标点,调用Astar全局路径规划器生成全局路径,全局规划器发布全局路径给局部路径进行路径规划,计算控制指令下发给机器人底盘。move_base节点将全局和局部路径规划程序通过状态机连接在一起,以完成导航任务,还维护两个用于完成导航任务的代价地图,一个用于全局规划程序,一个用于局部路径规划程序。整个框架设计如图6所示。 move-base状态机分为planning,controlling,clearing三种状态。planning是接受新目标与进行全局规划的整个过程,controlling是进行局部路径规划发出速度指令的行为,clearing是全局规划和局部规划失败或困住触发recovery行为的用来处理上述情况的异常。当move_base接收到目标终点请求,move_base调用makePlan函数进行全局规划,便启动Astar全局路径规划器,进行全局路径规划,规划完成将全局路径以话题通信的方式发布(publishPlan)出来,move_base状态机切换到controlling状态,改进的TEB路径规划器通过相关函数(setPlan)接收全局路径,里程计负责定位,激光雷达获得障碍物信息,以一定的频率进行局部路径规划,计算出控制指令,发布给机器人下位机控制器。 仿真和实际实验的对象是一个具备阿克曼转向机构的非完整约束机器人。机器人的运动学参数:机器人前轴虚拟转角限定范围为[-30°,30°],轴距L=0.9 m,最小转弯半径1.56 m。 仿真平台:stage。仿真计算机配置:CPU I7 主频2.6 GHz,6核12线程,局部路径规划频率为20 Hz。机器人参数如表1所示。 对权重参数调优后,搭建仿真环境进行测试。 仿真场景一:进狭窄巷道和机器人脱困 仿真分析:由图7(a)可知能规划出符合阿克曼机器人运动学的路径,轨迹曲率符合要求。由图7(b)可知该算法能规划出调头的路径而且满足阿克曼机器人的非完整约束和最小转弯半径约束。规划的路径符合仿真地图的实际情形。 图7 阿克曼机器人规划局部路径 仿真场景二:复杂迷宫地图场景 仿真分析:由图8、9可知,机器人能得到一条满足阿克曼运动学动力学从起点到终点的一条无碰撞路径。 图8 机器人路径规划过程展示 图9 路径规划结果展示 对配有16线激光雷达的真实机器人在封闭多墙体场景进行测试,测试的真实机器人如图10、图11所示。 图10 机器人规划过程 图11 规划结果精度测量 真车测试结果表明:阿克曼机器人能避开障碍物,能够基本到达设定的目标点,位置平均偏差约6 cm,航向角平均偏差约8°。实验次数设置为50次,在改进TEB算法之前,机器人受到明显冲击的次数为5次,概率为1/10,改进TEB算法后,添加加加速度约束后,整个导航过程中机器人没有受到任何冲击发生震荡,运动过程非常平顺,基本到达预期要求。 针对阿克曼机器人运动规划问题,提出了一种改进的TEB算法,并得到如下结论。 (1)建立了阿克曼机器人运动控制模型。 (2)提出了一种改进TEB算法,将加加速度约束添加到TEB算法中,减少加速度突变带来的冲击,提高运动的平顺性。 (3)将该改进算法在阿克曼机器人应用,并在stage仿真环境中实现,最终在真实机器人上进行了测试和应用。不仅验证了改进的TEB算法的有效性,而且在阿克曼机器人上进行了有效应用。 该算法可广泛应用于阿克曼机器人的局部路径规划中,也可广泛用于自动驾驶汽车自动泊车领域。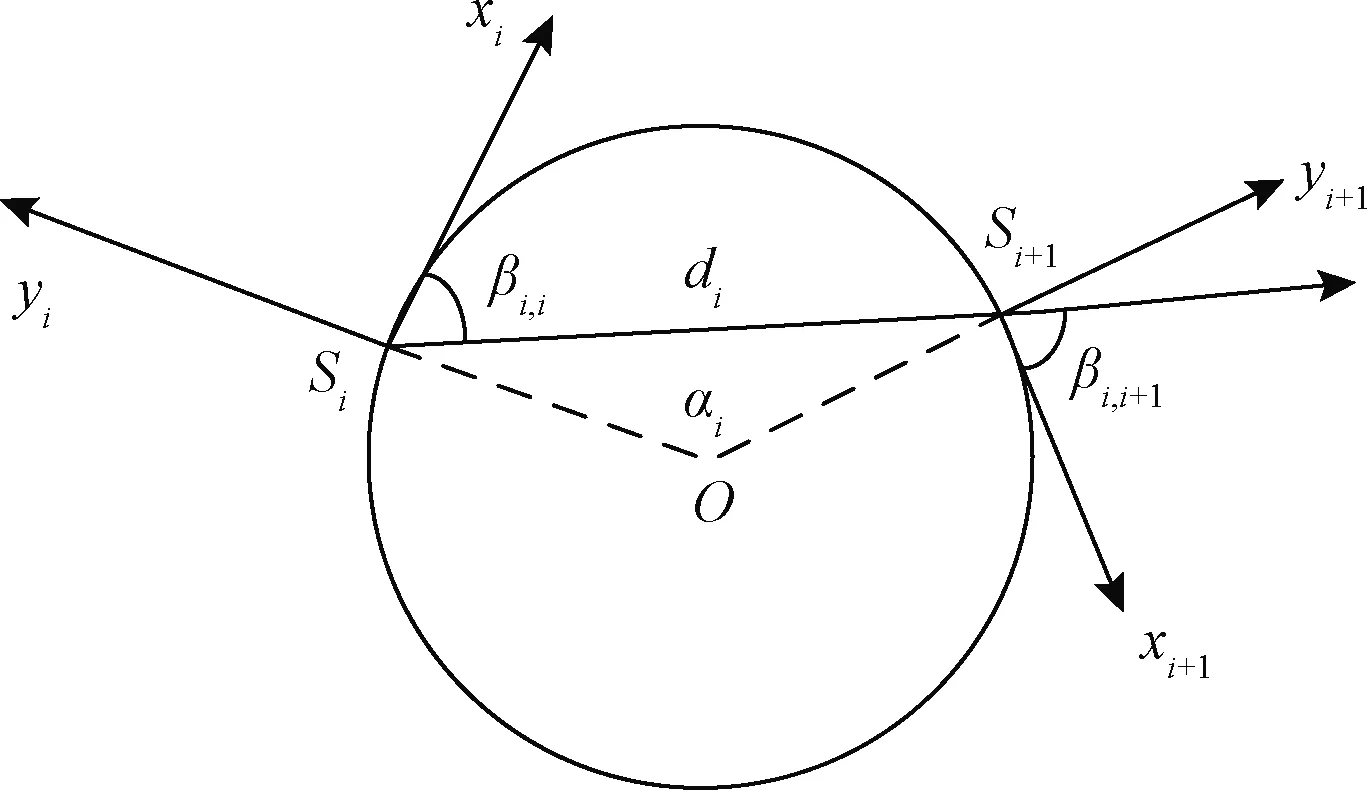
2.2 TEB算法求解模型的构建
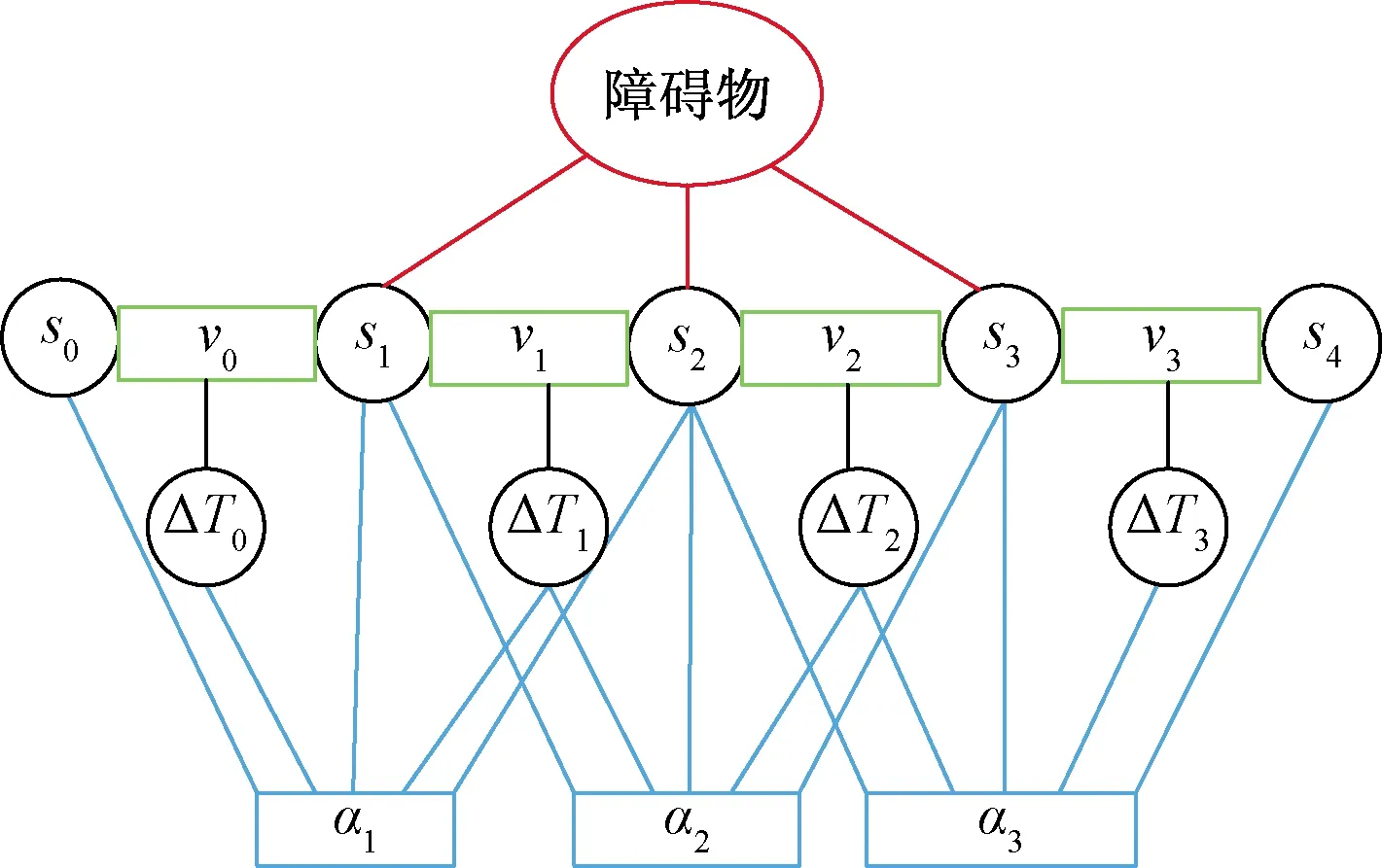

2.3 改进TEB约束条件
3 阿克曼机器人运动规划框架设计
4 仿真实验和真车测试实验
4.1 仿真实验
4.1 真实机器人实验


5 结论与展望

