基于无限大平行板的修正模型精确测量真空电容率

梁 燕，孙煜婷，刘凡凡，刘一平，岑 剡

(1．中国科学技术大学 物理实验教学中心，安徽 合肥 230026；2．复旦大学 物理学系 物理教学实验中心，上海 200433)

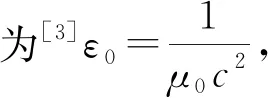
因此，本文提出考虑平行板电容器两极的平行性、边缘效应和分布电容的修正模型，并介绍通过实践总结出的易操作的调试两极板间距的零点实验方法，可使真空电容率ε0的实验值偏差降至0.6%以下，提高了真空电容率ε0的测量精度.

1 实验原理

从理论上考虑平行板电容器两极板的非平行性、边缘效应和分布电容的修正模型. 设两极板是边长为L的正方形，由于极板大小有限，需考虑其边缘效应；两极板难以完全调节平行，需考虑其非平行性，实验调节其两极间的夹角为θ，如图1所示. 对于该模型可根据文献[12]的理论，先用保角变换将非平行板电容器变换成复平面空间里的平行板电容器，再对其运用施瓦兹-克里斯多菲(Schwarz-Christoffel)变换进行计算[13]. 若两极板间电势差为V0，则可根据上述方法计算得到边长为L，上下极板最小间距为d时的正方形极板上所带总电荷Q为

(1)

式中ε0为真空电容率，d为极板间距离.

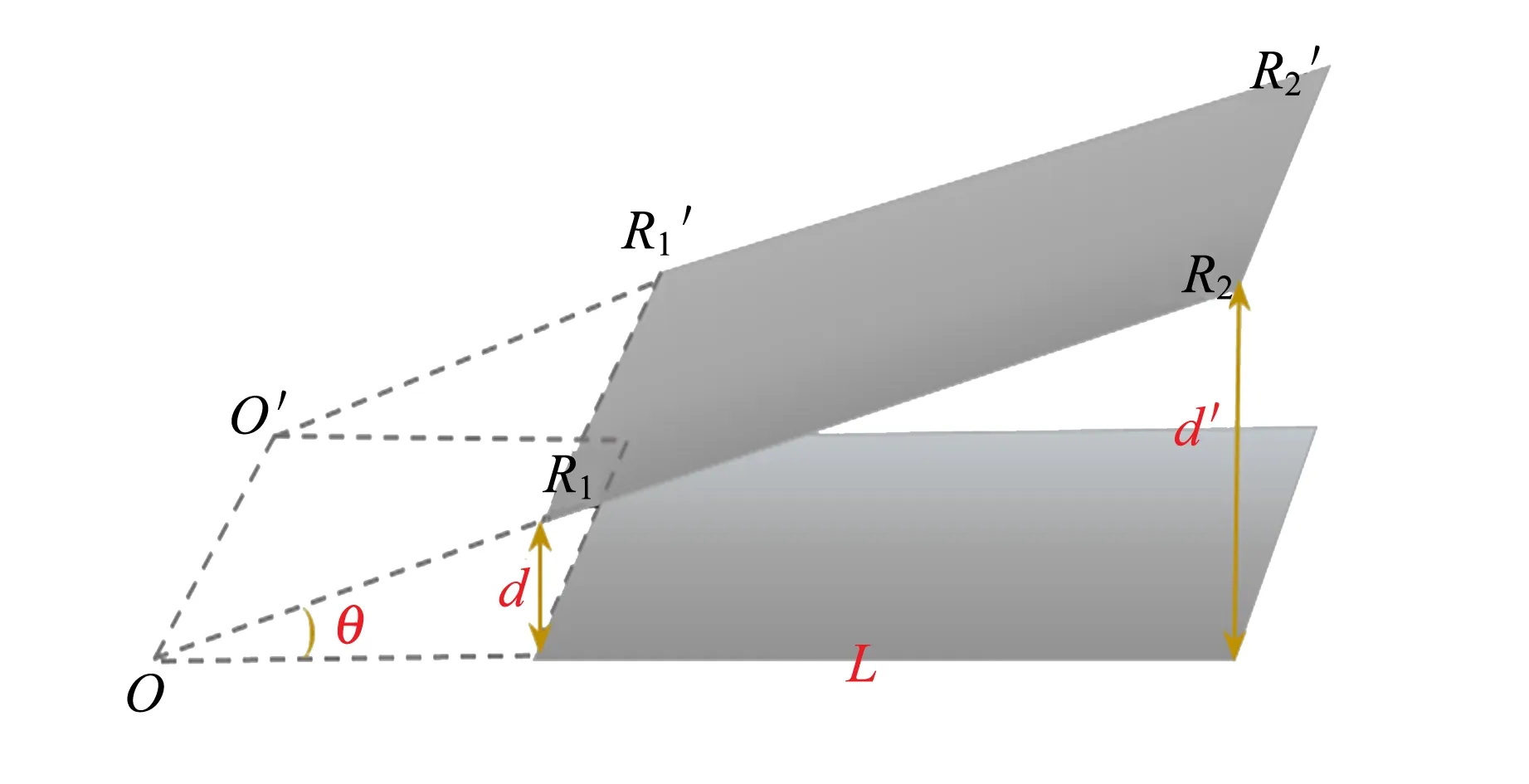
图1 极板非平行时的电容模型

由于变换前后极板间电势差与极板所带电荷量不变，则电容为

(2)

在此基础上，考虑到测量过程中分布电容C′存在，式(2)进一步修改为

(3)

上述电容器模型的建立考虑了两极板的不平行、极板面积大小有限以及测量过程中带来的分布电容，此模型更加接近实际的平板电容器，用它测量计算真空电容率更接近客观值.

2 实验方法及仪器

实验中所用平行板电容器由美国南卫理工会大学(Southern Methodist University，SMU)叶竞波教授团队设计(图2)，该平行板电容器由上下金属极板构成，其中下极板通过鼓轮Z向(垂直极板方向)做高低调整，这样整个下极板可以平行上下移动，以方便改变上下极板之间的距离d，四边4个立柱高低可调，以方便改变极板间角度.

实验中为了准确测量电容C需要将平行板电容器和电容表分别短路放电，从而保证极板和电容表内没有净电荷. 两极板的间距d可通过电容突变法测量鼓轮零点来确定. 具体测量方法为：先缓慢缩小极板间距直至两极板正好接触，可观察到电容表读数为无穷大，此时记录鼓轮读数为鼓轮零点TT0. 两极板的间距d可通过测量鼓轮读数TT减去鼓轮零点TT0获得.

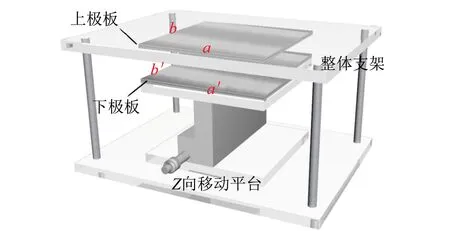
图2 实验所用平板电容示意图

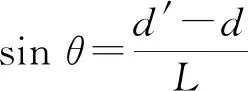
(4)

实验研究了夹角θ分别为0.002,0.004,0.006,0.008,0.010 rad时，板间距d和电容值C的对应关系，由于实验中调节了夹角φ为0，因此可通过式(3)计算真空电容率ε0，而式(4)则用于不确定度分析.

3 实验结果与讨论

首先做出实验数据散点图，再根据式(3)建立非线性拟合曲线模型，以板间距d为自变量，以电容C为因变量，以其他量为参量进行拟合，结果如图3和表1所示.

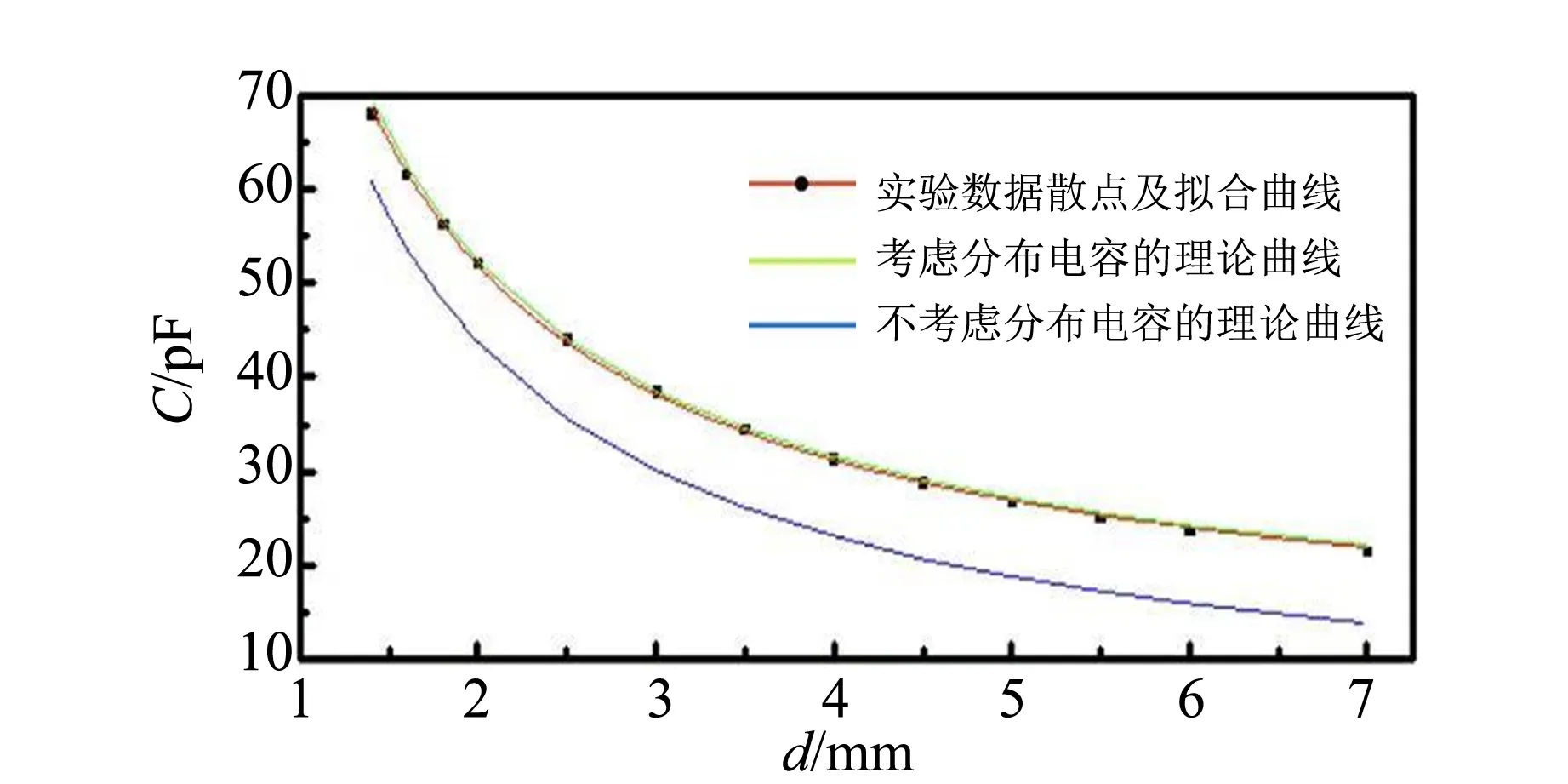
(a)θ=0.002 rad

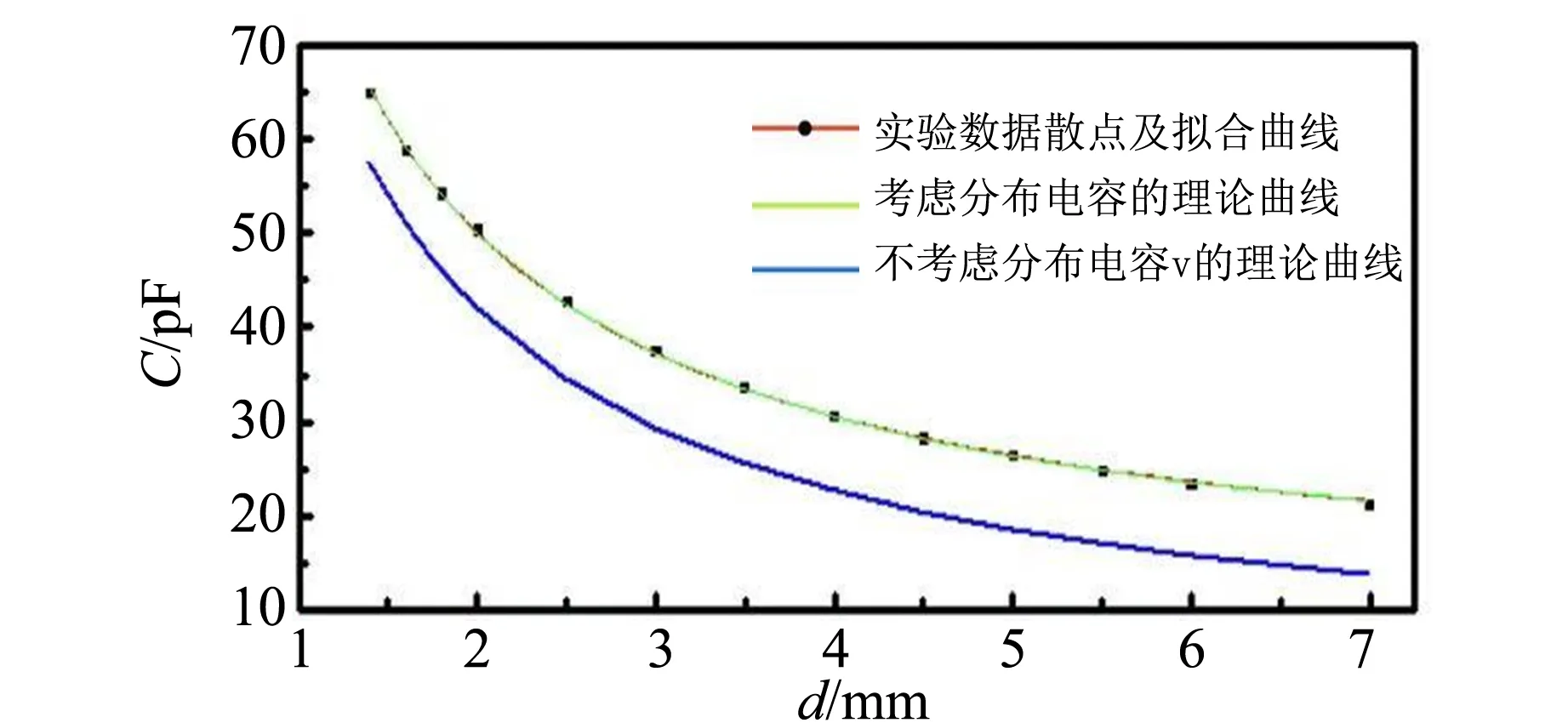
(b)θ=0.004 rad

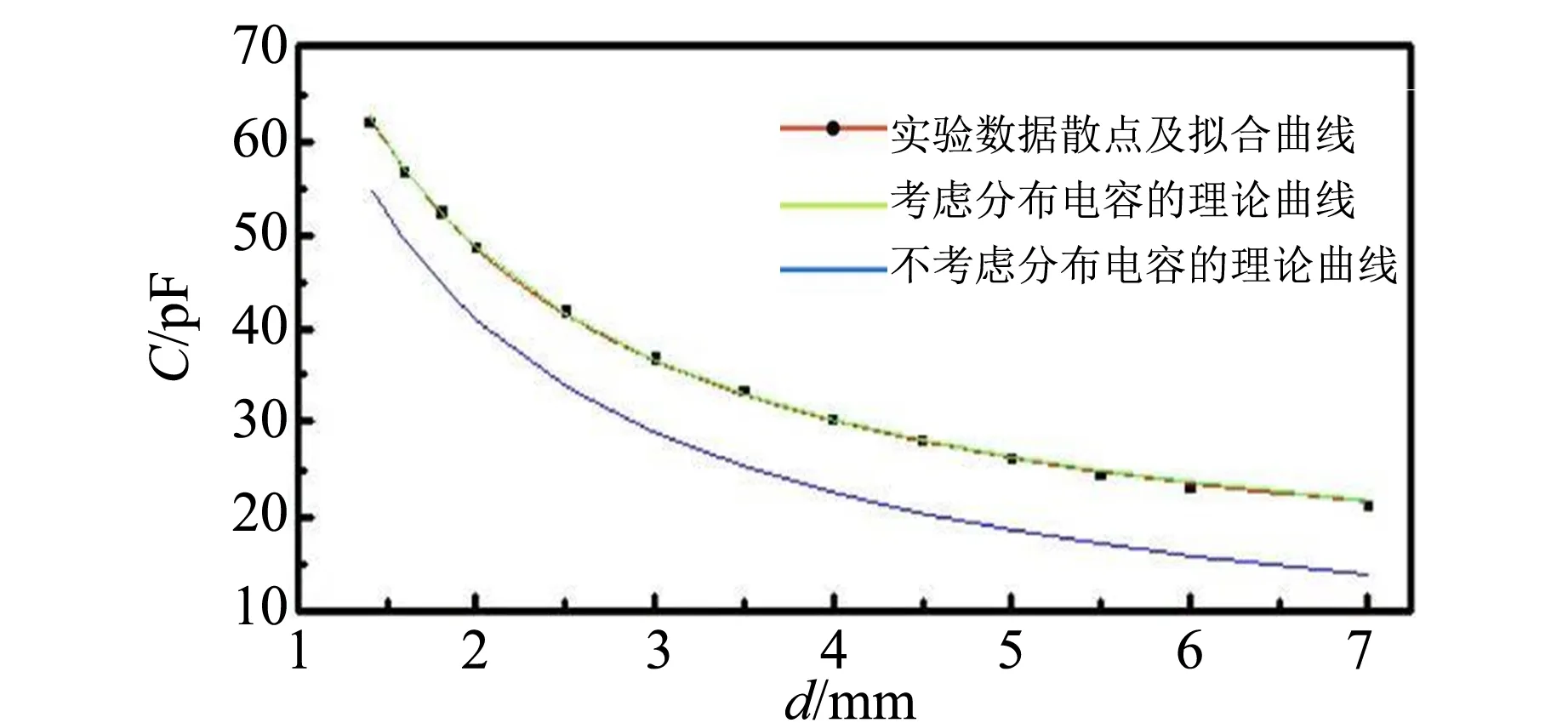
(c)θ=0.006 rad

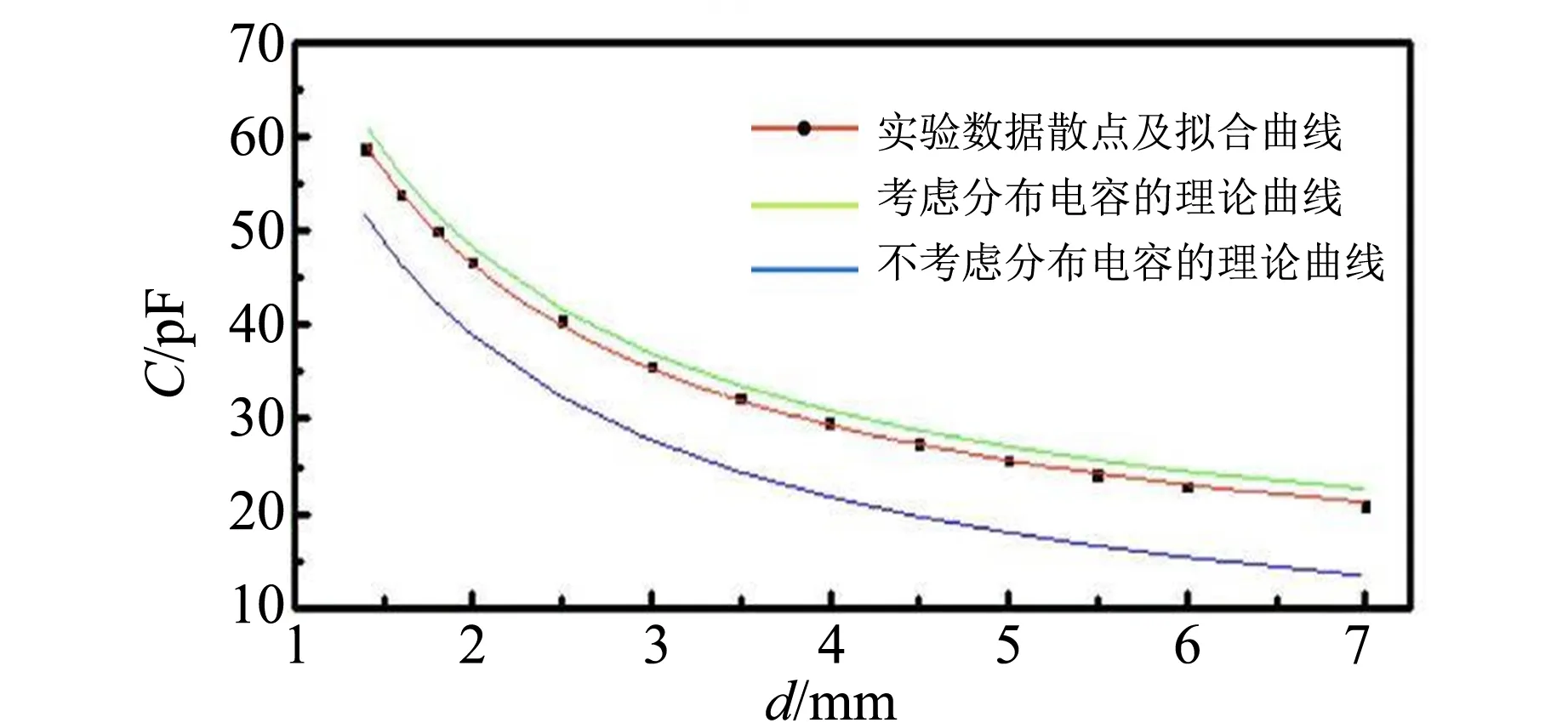
(d)θ=0.008 rad

(e)θ=0.010 rad图3 当两极板间夹角θ不同时，电容C和板间距d的关系拟合图

表1 不同极板夹角对应的真空电容率实验结果

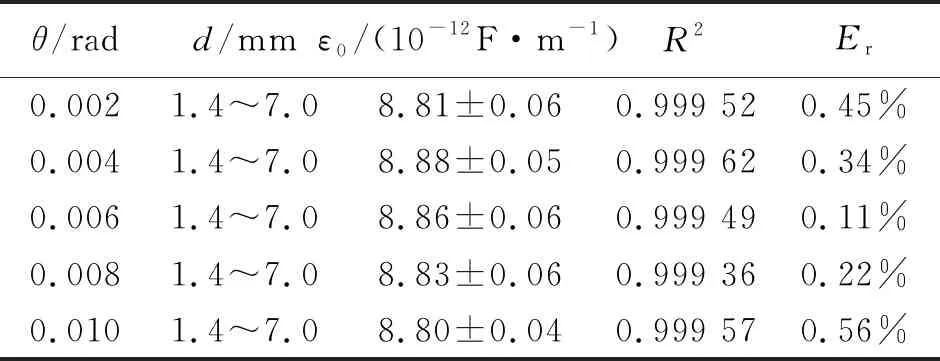
θ/radd/mmε0/(10-12F·m-1)R2Er0.0021.4～7.08.81±0.060.999 520.45%0.0041.4～7.08.88±0.050.999 620.34%0.0061.4～7.08.86±0.060.999 490.11%0.0081.4～7.08.83±0.060.999 360.22%0.0101.4～7.08.80±0.040.999 570.56%

图3中红线是实验数据拟合的曲线，蓝线是根据不考虑分布电容的式(2)画出，绿线是根据考虑分布电容的式(3)画出，可以看出根据式(3)的理论模型的绿线与实测数据拟合的红线有很好的的拟合程度，其中相关系数R2与1非常接近，见表1. 在相同夹角下，红线与蓝线差值在各个d上基本一致，说明分布电容的存在，在数据处理中必须要考虑，由表1中看出，实验值的最好结果与国际科学协会公布的基础物理学常量中的真空电容率ε0相对偏差仅为0.11%.

图3和表1的结果说明：1)建立的理论模型和实际吻合度高，合理解释了实际情况；2)测量过程中分布电容需考虑，反映在非线性拟合函数最后会有待定参数项；3)在本科实验教学中，能够通过简单的模型搭建，可行的实验方法可以得到准确度较高的真空电容率，可以用此方法拓展，设计实验方法测量电介质的相对电容率.

实验中对板间距d的测量范围进行了限制，这是通过对ε0进行不确定度分析得到的. 对ε0进行不确定度分析可以获得各测量量对不确定度的影响，从而减小因实验测量造成的ε0的不确定度.

由式(4)可知，夹角θ的不确定度u(θ)、夹角φ的不确定度u(φ)、板间距d的不确定度u(d)、电容C的不确定度u(C)和分布电容C′的不确定度u(C′)对真空电容率ε0的不确定度u(ε0)都有影响，而该影响可通过标准不确定度的传递公式进行计算，形式如下：

(5)

为便于描述不同物理量的不确定度对于u(ε0)的贡献，可利用

将式(5)改写成

u2(ε0)=Δε02(d)+Δε02(θ)+Δε02(φ)+

(6)

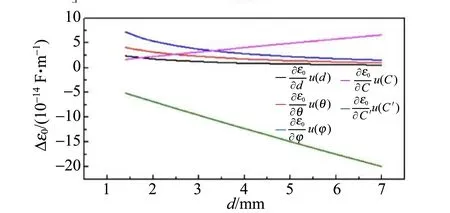
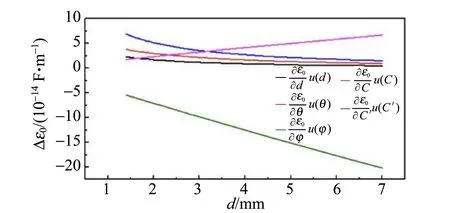
通过式(6)的计算，可以得到当角分别度为0.002～0.010时，由d,θ,φ,C,C′的不确定度(图4中对应的不同颜色曲线)引起的对应真空电容率计算值的变化量Δε0随板间距d变化的关系图，如图4所示.

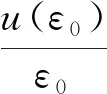
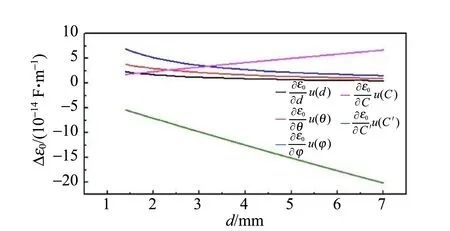
(a)θ=0.002 rad

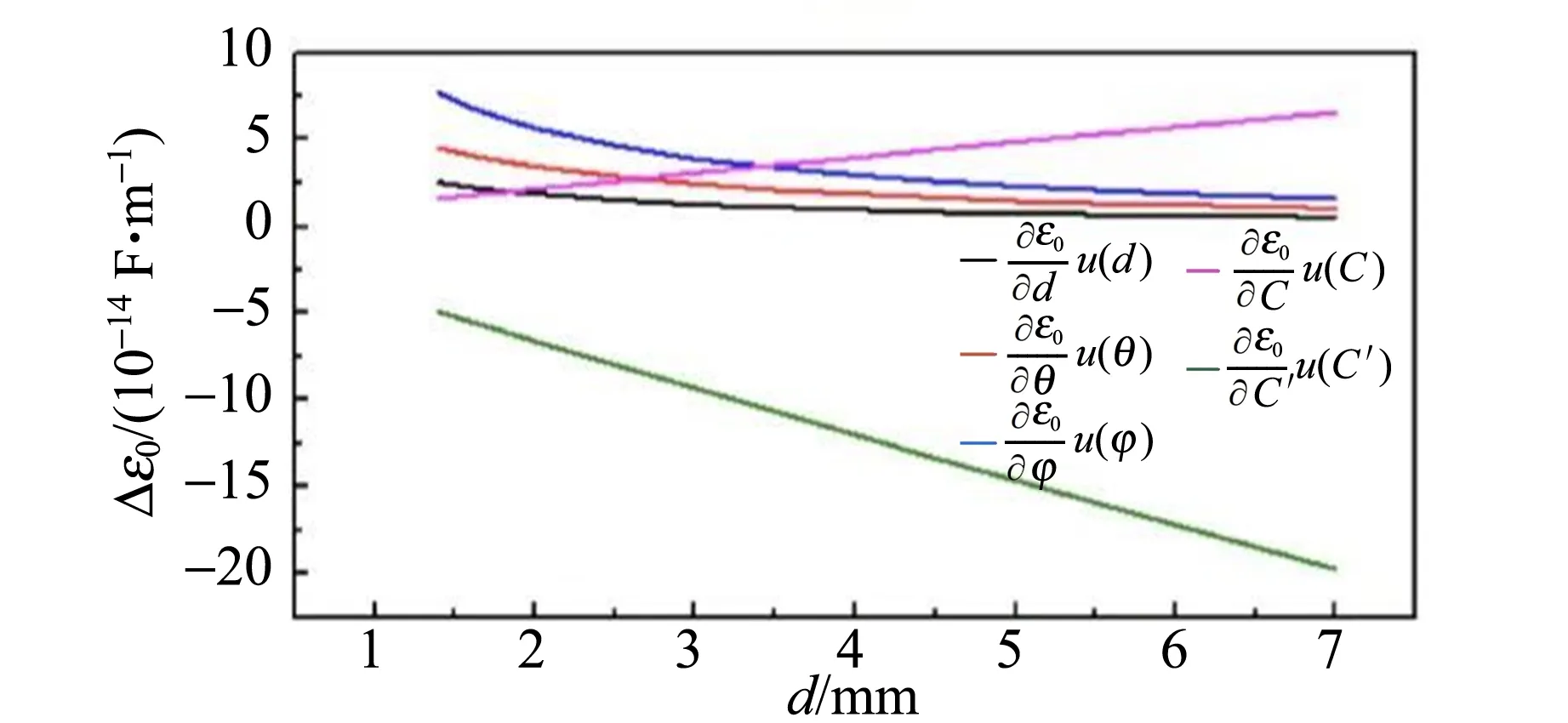
(b)θ=0.004 rad

(c)θ=0.006 rad

(d)θ=0.008 rad

(e)θ=0.010 rad图4 当两极板间夹角θ不同时，由d，θ，φ，C，C′的不确定度引起的真空电容率计算值的变化量Δε0随板间距d变化的关系图

4 结束语

考虑到边缘效应和分布电容的非平行板电容公式模型，提出了更为精准的测量真空电容率ε0的方法，并指出了是否考虑非平行、边缘效应和分布电容是影响测量精度的主要原因. 进一步修正了模型，并提出了通过分析不确定度以限定板间距测量范围的方法，从而进一步提高实验结果的精度，使真空电容率测量相对偏差下降到0.6%以下.