基于粒子图像测速技术的涡旋简易测控

吴佩芳,张润生,杜 淼,吴利灿,刘宇帆,邵志刚

(华南师范大学 物理与电信工程学院 物理国家级实验教学示范中心，广东 广州 510006)

对于涡旋的研究，自Rankine组合涡旋模型问世以来，科学家们就一直试图利用简化的纳维-斯托克斯方程以及流体测速设备对于不同的涡旋进行理论或实验的研究. 对于立轴涡旋来说，也有科学家开始陆续进行对其理论分析、模型试验以及数值模拟的探索[1-2]，Tomomi等人更是研究了水流上升气泡与涡核的相互作用[3]. 本文在立轴涡旋理想数学模型基础上设计了相关的涡旋产生装置，并基于PIV粒子图像测速技术测出涡旋的相关物理量，进行对立轴涡旋的简易测控，结果验证立轴涡旋理想数学模型的正确性，同时为初次接触涡旋的人们提供基础理论与实验指导.

1 实验原理

1.1 立轴涡旋数学模型

涡旋的特性参量主要包括涡旋半径、涡量、最大切向速度等. 文献[4]提出，常见的表面涡旋由涡旋的有旋和无旋2部分组成，同时给出了立轴涡旋的理想流体数学模型，如图1所示.

假设立轴涡旋为轴对称流动Δt

(1)

其中，vk为切向流速vθ、径向流速vr或轴向流速vz，p为静水压力.

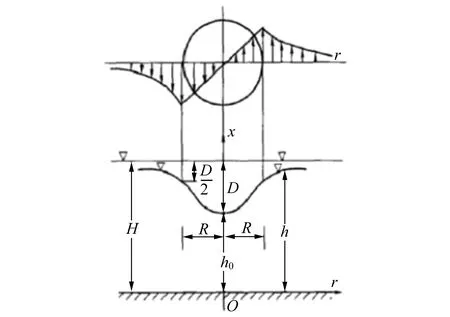
图1 立轴涡旋理想数学模型

若在水深为H的水面上出现恒定半径为R,角速度为ω的立轴涡旋，则切向速度vθ=ωr，由于水体具有黏性，在r≥R以外的水体也会被带动从而绕着立轴涡旋中心做圆周运动，其切向速度vθ随着r增大而减小，即

(2)

且王英奎等对于立轴涡旋公式进行了改进[5]，得vz=0；而且，表明在有旋流动区域

(3)

在无旋流动区域

(4)

张兰丁等人则在上述立轴涡旋理想流体模型的基础上给出了精确满足N-S方程的理论解[6]，其中并未进行任何假设，同时指出根据有旋部分的旋转角速度ω结合涡旋半径R可以计算出涡深为

(5)

1.2 PIV粒子图像测速技术原理

在涡旋流场中撒入示踪粒子，使之漂浮于流场表面，利用工业相机CCD记录1组具有固定时间间隔的图像，通过对相邻时间间隔的2张流场图像进行数据处理，则可获取流场中的示踪粒子分布图像并进行对应的数据处理.

贾辉等人给出了一种计算涡旋速度的方法[7]. 如果已知某示踪粒子在时刻t1后经过时间Δt后在时刻t2的对应图像，则可计算出Δt时间内粒子运动的位移，从而根据速度-位移公式流体速度矢量，从而表征涡旋表面流体速度. 计算公式为

(6)

(7)

则速度矢量大小和方向为

(8)

(9)

2 实验装置

2.1 涡旋发生控制系统

由于水从漏水口往下漏与阀门壁摩擦，水流的速度变小，外圈的水向中心补充导致水流呈涡旋旋进，同时还有水泵冲进的水为涡旋源源不断地提供动力，使其不会慢慢耗散，协同水泵进水和漏水口大小可以控制涡旋的大小和速度.

为了保证涡旋稳定，引入了通心圆筒，圆筒内巧妙地连接了2个水泵，通心圆筒不仅起到隔绝和缓冲的作用，保证实验得到的涡旋稳定且易测量，而且节省了经费.

装置如图2所示，上部分是方形水槽(内含通心圆筒)即涡旋产生控制部分，漏水口和进水口都在上部分，下部分是储水箱，水通过漏水口漏在储水箱里，然后被水泵泵上方形水槽，这样既有助于形成涡旋，也可以保持涡旋水面的稳定.

图2 实验装置图

2.2 涡旋测量系统

PIV粒子图像测速技术是一种瞬态流动平面二维速度场测试技术，能对一定平面内的速度场分布进行测量[8]. 其原理是在被测量的流场中加入示踪粒子，用激光照亮流场，在照亮片区的法线方向附近用高速摄像机记录流场中示踪粒子的图像，再采用互相关算法对图像进行处理得到流场速度矢量分布图. 该方法克服了以往其他测量方法只能单点测量的缺陷.

2.3 实验器材

实验器材：

1)方形水槽1个，尺寸为25 cm×25 cm×40 cm，4个侧壁的左下角均开有9 mm的小孔，用于接入水管；在水槽底部开有漏水口，接入水阀门，可以控制漏水的速度.

2)水泵4台，选用了2台扬程为15 m的水泵、1台扬程为10 m的水泵、1台扬程为1 m的水泵，分别接上8 mm外径的水管. 通过水泵之间开关的搭配，可以实现涡旋的稳定形成.

3)水阀门1个，水阀门实用直径约2 cm，通过开关水阀门实现涡旋大小的控制，也可以调节水面的稳定.

4)PVC软管(水管)4根，外径为8 mm，连接水泵与方形水槽.

5)储水箱1个，储水箱用来储存发生涡旋用水，漏水口漏水漏在储水箱中，水泵也从储水箱中抽水.

6)外置纸箱1个，提供黑暗的环境.

7)PVC塑料通心圆筒1个，通心圆筒底部侧面开有2个小口，用于连接水管，使得在圆筒内形成涡旋.

8)铁丝圈1个，用于固定住通心圆筒，不会使通心圆通在内外水压的挤压下变形，进而维持涡旋的形状.

9)5 mV激光器1台，照亮示踪粒子，使得相机能够清晰地拍到，也方便软件对其进行图像处理和识别.

10)CCD高速相机1部，记录示踪粒子运动地轨迹与图像.

11)示踪粒子选用塑料粒子，作用为跟随水体做涡旋的运动.

12)双凹柱透镜1个，将激光源拓展成扇形光源，照亮整个涡旋水面.

13)Virtual Dub软件，将视频素材进行剪辑、分帧，获得连续的清晰的图片.

14)Matlab PIVlab工具包，将进行图像处理，模拟流场的速度矢量图.

3 结果及分析

3.1 实验步骤

1)关闭方形水槽底部的漏水阀门，打开4台水泵，向水槽底角进水口泵水，其中有2台水泵通过接水管接入水槽内的通心圆筒中.

2)待水位上升30 cm后，打开水槽底部漏水阀门，控制漏水速率，保持水面维持稳定并形成稳定涡旋.

3)接通线性激光并照射涡旋表面，撒入示踪粒子，利用CCD相机拍摄清晰视频.

4)关闭其中1台水泵，使液面高度水面下降到1 cm，打开水泵让液面维持稳定，重复步骤3)，每降低1 cm测1组数据，测10组数据.

5)利用Virtual Dub软件将获得的不同高度的涡旋视频进行剪辑、分帧，获得连续的、清晰的图片.

6)利用Mabtlab PIVlab互相关算法对获得的图片进行图像处理，模拟出流场的速度及涡度矢量场，得到不同高度、距离涡旋中心不同距离的三维平面内的涡度、速度环量等涡旋相关物理量的具体数据.

3.2 实验效果

3.2.1 涡旋发生效果

图3(a)为产生稳定涡旋时的侧视图，图3(b)为在激光器照射下撒入示踪粒子后涡旋的效果图.

(a)稳定涡旋侧视图

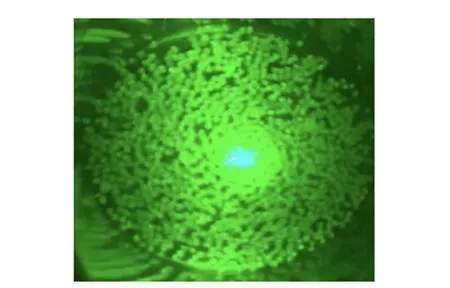
(b)撒入示踪粒子后涡旋侧视图图3 涡旋发生效果

3.2.2 涡旋剪辑效果

图4为应用Virtual Dub将得到的涡旋视频进行分帧处理，得到的一系列连续的分帧图片.

图4 Virtual Dub处理后的分帧照片

3.2.3 实验结果

首先，对所得的分帧图片进行流场分析. 为了减小实验误差，将激光曝光以及气泡部分进行了Mask处理(Mask选中区域将在后面的运算中不会被分析处理)，多次傅里叶变换后可得到稳定涡旋的涡旋流场流量图.图5为通过PIVlab得到稳定涡旋在液面高度为25 cm和30 cm的涡旋流场图.

(a)25 cm

(b)30 cm图5 不同液面高度下涡旋流场图

然后跟踪单个粒子的运动轨迹，图6为在液面高度为30 cm时画出的单个粒子从涡旋外圈向中运动的轨迹图.

图6 液面高度30 cm粒子运动轨迹图

其次，同时跟踪多个粒子，得到涡旋的流线图，同时处理得到涡旋二维平面速度及涡度矢量分布图,如图7所示.

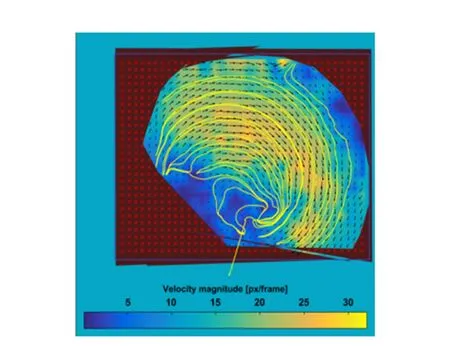
(a)30 cm高度流线及速度分布图

(b)30 cm高度流线及涡度分布图图7 液面高度30 cm粒子流场特征图

最后，从图像处理后的涡旋流场图中可以清晰地看到涡旋各处的流速矢量方向、各粒子的运动轨迹以及确定涡旋中心，对处理后的涡旋流场图采用自适应互相关法，选中过涡旋中心的1条直线，分析其上的涡度及速度分布，通过去噪处理，模拟得到贴合实际情况下的涡度及速度分布，其中取涡旋高度30 cm及涡旋高度25 cm数据，如图8所示，图中，黑色虚线为实际得到数据，蓝色实线为去噪模拟得到的涡度及速度分布.

通过对比可以看出，对于同一稳定流体涡旋，越靠近涡旋中心，流速越小，涡度越大；涡旋高度越高，涡旋表面速度越小.

(a)液面高度25 cm过涡旋中心直线上的速度分布

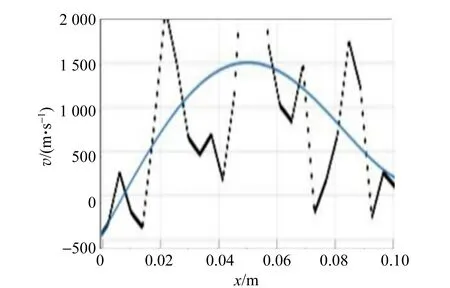
(b)液面高度25 cm过涡旋中心直线上的涡度分布

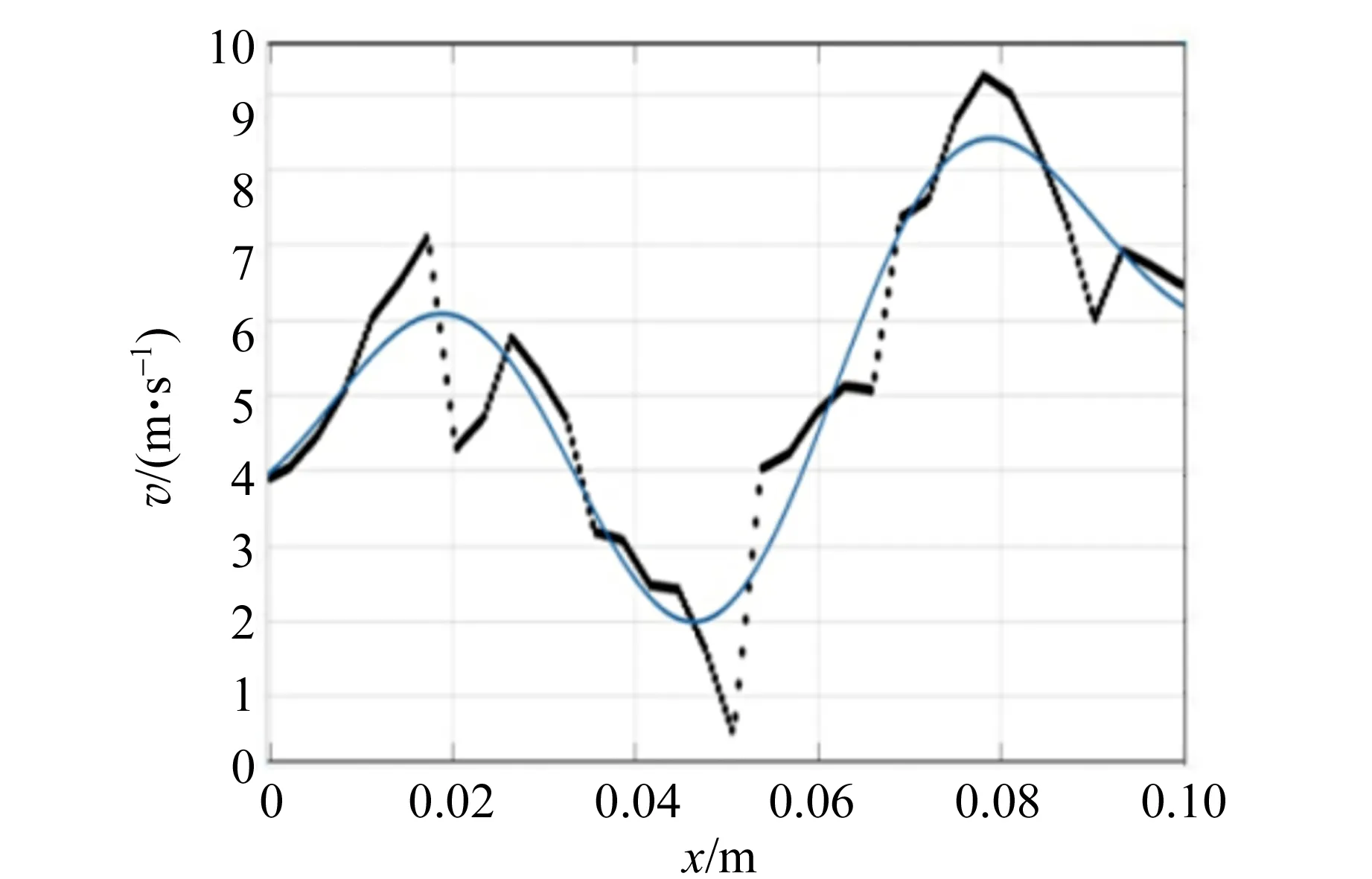
(c)液面高度30 cm过涡旋中心直线上的速度分布

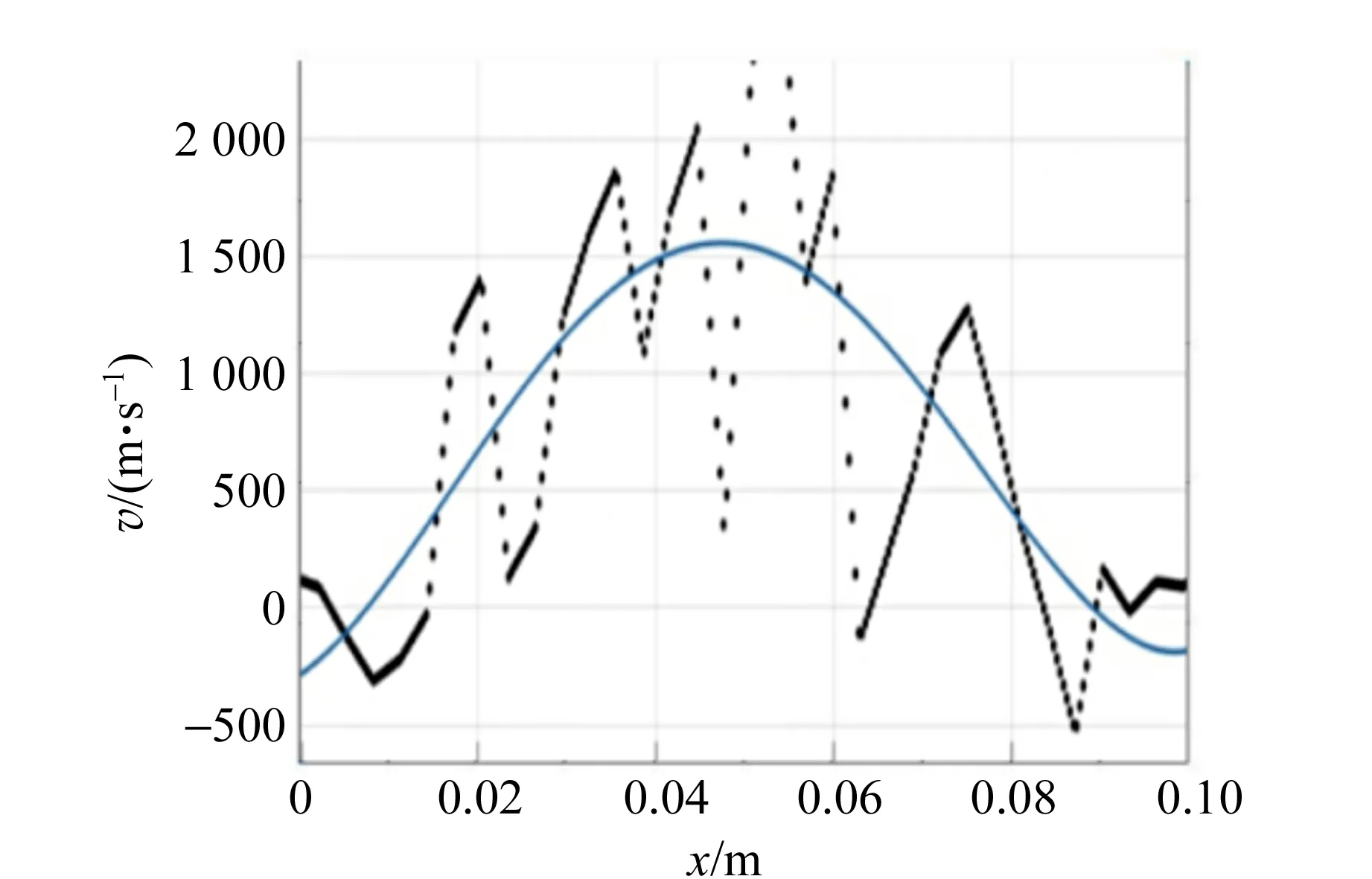
(d)液面高度30 cm过涡旋中心直线上的涡度分布

图8 不同高度过涡旋中心的速度、涡度分布图

4 结 论

在立轴涡旋理想数学模型基础上设计了涡旋产生装置，生成稳定且可控的流体涡旋，通过PIV粒子图像测速技术对于立轴涡旋在不同液面高度下的速度和涡度进行实验分析. 实验结果表明，对于同一稳定流体涡旋，越靠近涡旋中心，流速越小，涡度越大；越远离涡旋中心，流速越大，涡度越小. 对于同一稳定流体涡旋，涡旋高度越高，涡旋表面速度越小，涡旋高度越低，涡旋表面速度越大. 实验结论与立轴涡旋理想流体速度环流数学模型的结果相似[1]，验证了立轴涡旋理想数学模型的正确性.