模糊遗传粒子滤波算法研究∗

刘淑波 张 园 初俊博 史新鹏 邓加川

（海军大连舰艇学院基础部 大连 116018）

1 引言

在实际应用中，大量问题都属于强非线性和非高斯分布的情况。粒子滤波是一种新型的被广泛适用于非线性、非高斯随机系统的滤波估计算法，相对于其他非线性滤波算法，它的实用性更强［1～4］。

但是基本粒子滤波随着滤波时间的增加避免不了会出现大量计算浪费在对估计不起任何作用的微小粒子上，为了解决这种问题，引入重采样来去除那些权值小的粒子，保留并复制那些权值较大的粒子。重采样带来的负面作用是具有较大权值的粒子被多次选取，从而损失了粒子的多样性。

针对非线性观测条件下的机动目标跟踪问题，在基本的粒子滤波算法中引入模糊遗传算法，得到一种改进的粒子滤波算法——模糊遗传粒子滤波（FGA-PF）算法，以减小估计误差，然后将该算法用于二维仿真环境中的机动目标跟踪问题。仿真中，将其与基本的粒子滤波算法和基于重要密度函数选择的改进粒子滤波算法UPF算法进行比较，证明了算法的有效性和优越性。

2 系统数学模型

考虑雷达观测在极坐标下进行，这时系统的状态方程和观测方程分别如式（1）和（2）所示［4］。

3 算法设计

3.1 初始化

由先验概率p(x0)产生初始粒子，并令其权值为1N。

3.2 状态预测

利用状态方程预测下一时刻的粒子:

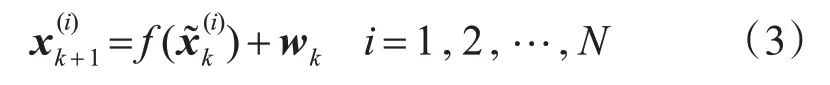
3.3 权值更新

在k时刻计算粒子权值，k=1，2，…，N

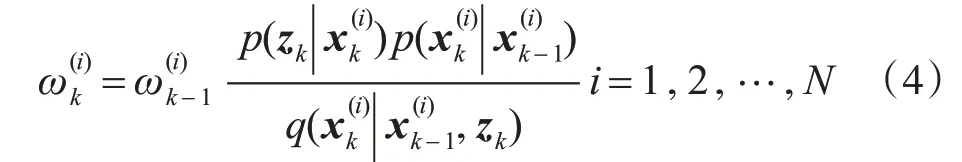
并且归一化:

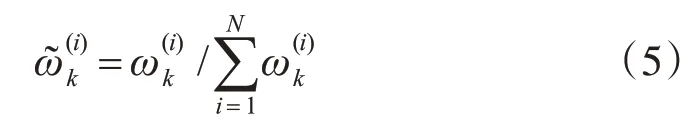
3.4 智能优化判断

3.5 模糊遗传运算［5～10］

3.5.1 选择运算

3.5.2 交叉运算

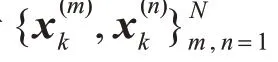
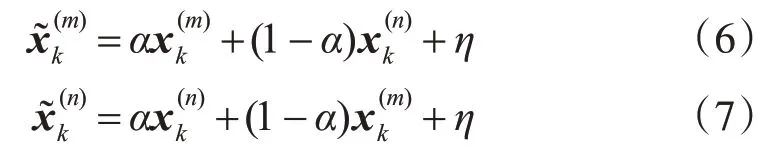
其中，η～N(0，σ)，α～U(0，1)。

3.5.3 变异运算

采用算法3 模糊推理系统分别算出变异概率pm，产生随机数u～U(0，1)。若u＜pm，从粒子库中随机选择一枚粒子，按下式进行变异运算:

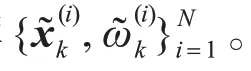
3.6 估计输出

状态估计:

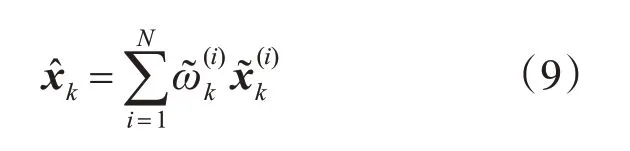
协方差估计:

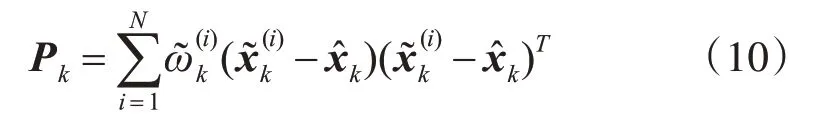
3.7 下一时刻，转到步骤3.2

4 模糊推理系统设计

本文设计两套模糊推理系统，分别推理得到输出变量交叉概率pc和变异概率pm。

4.1 模型推理系统输入变量的计算

定义两套模糊推理系统的输入量分别为ΔE，Δfc以及ΔE和Δfm。其中，ΔE为相邻两代群体适应度均方差的改变量，定义为

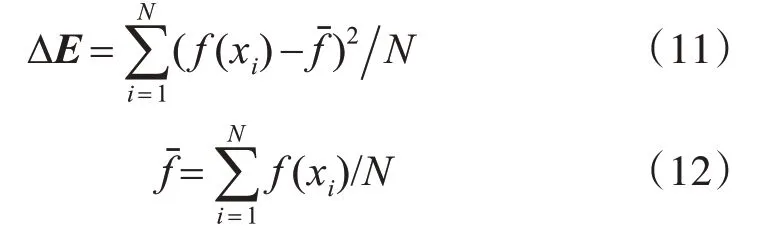
其中，f(xi)为个体i的适应度，为平均适应度。

Δfc为待交叉个体适应度较大者的适应度与最佳适应度之差。

Δfm为待变异个体的适应度与最佳适应度之差。

模糊推理系统输入变量ΔE，Δfc和Δfm的模糊子集均为S（小）、M（中）、B（大）。选定模糊子集的隶属函数为高斯型函数，如图1所示。

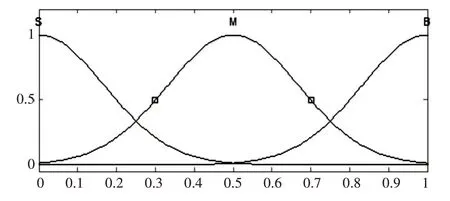
图1 各输入变量的隶属函数

4.2 交叉概率和变异概率的计算

输出变量为交叉概率pc和变异概率pm。定义输出变量交叉概率pc的模糊子集S（小）、M（中）、B（大），另一输出变量变异概率pm的模糊子集S（小）、M（中）、B（大）、HB（很大），也采用高斯型函数作为隶属函数，如图2所示。

图2 输出变量的隶属函数

则根据模糊推理系统的推理特征，有如下一些关于交叉概率和变异概率的模糊规则存在。

交叉概率和变异概率的模糊规则均为27 条，具体如下:

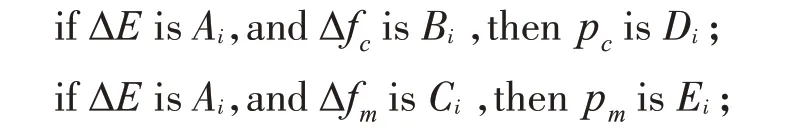
其中，i=1，2，…，27，Ai、Bi、Ci、Di和Ei是定义在ΔE、Δfc、Δfm、pc和pm论域上的模糊集。

根据这些模糊规则，由模糊推理系统可以得到k时刻的交叉和变异概率。

5 仿真结果

由于本文研究的是非线性滤波算法，因此，仿真场景选择了典型的非线性轨迹，即转圈运动［11-12］。选择[3 0000m，0m] 为其初始位置，[4 00m/s，0m/s]为其初始速度，a0=30m/s2为其初始切向加速度，仿真时间为80s。

仿真中，设量测噪声为零均值的高斯噪声，其标准差为diag[150m 0.3°]。其它参数选择如下:amax=80m/s2，采样周期T=1s。

为了验证本算法的性能，将其与基本PF 算法和UPF算法进行比较。

分别对各算法进行Matlab仿真，可以分别计算出其位置、速度均方根误差（其结果如表1 所示，x方向、y方向的仿真曲线如图3和4所示）和平均计算时间（如表2所示）。

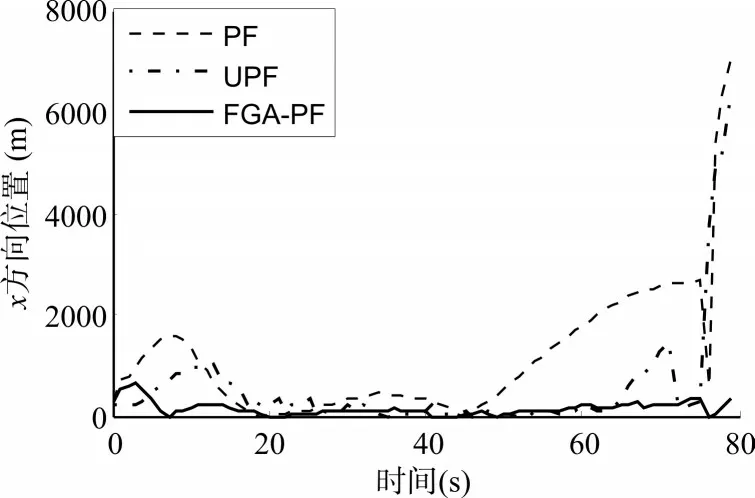
图3 x方向位置均方根误差曲线

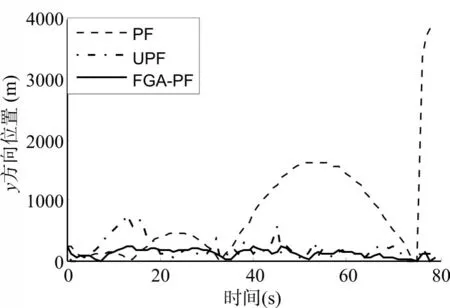
图4 y方向位置均方根误差曲线

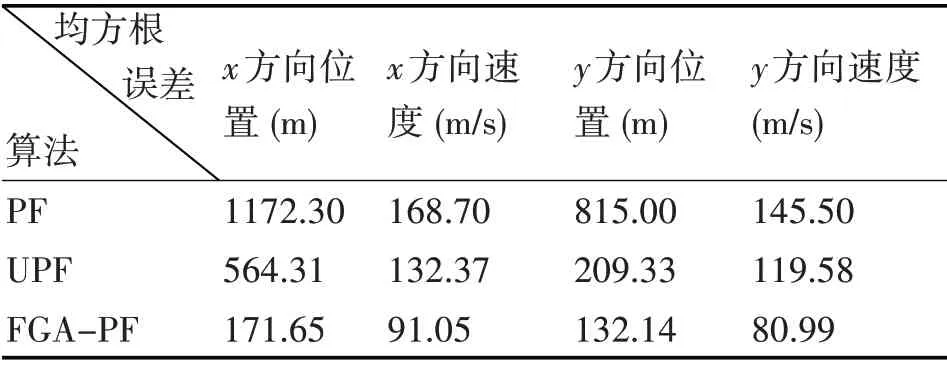
表1 100次蒙特卡罗仿真结果

表2 100次蒙特卡罗仿真平均计算时间

由仿真曲线和结果可以看出，与基本PF 算法相比，FGA-PF算法的跟踪精度大幅提高。

与UPF算法相比，本算法能够提高位置和速度跟踪精度的同时，伴随着计算复杂度和计算时间大幅降低。其平均计算时间只有UPF算法的1%。

6 结语

该算法与基本的PF 算法相比，跟踪精度大幅提高；与基于重要密度函数选择的改进粒子滤波算法——UPF算法相比，提高跟踪精度伴随着大幅缩减计算时间。因此，FGA-PF 算法是一种非常实用的非线性滤波方法，具有较高的跟踪精度和较低的计算成本，同时也为粒子滤波的其它智能优化改进提供了工程支持。