绿化修剪车避障工作装置运动学分析

周小浩，焦生杰，王庆先

(1.长安大学 公路养护装备国家工程实验室，陕西 西安 710064；2.江苏集萃道路工程技术与装备研究所，江苏 徐州 221004)

0 引 言

传统绿化修剪车在作业过程中遇到线柱、标识牌、反光柱等障碍物时，都是手动操作机械臂避障。若操作不当，可能会导致与障碍物发生碰撞，从而损坏割草装置，存在安全隐患。同时，手动操作降低了绿化修剪车的作业效率。避障绿化修剪车的避障工作装置能够检测、自动避开绿化修剪车作业过程中的障碍物，与传统绿化修剪车相比，具有安全、高效、智能等优点[1]。

绿化修剪车机械臂的灵活性和运动的平稳性在很大程度上决定着绿化修剪车的避障性能，因此对工作臂的运动学分析具有重要的工程应用价值[2]。本文通过矩阵分析法[3-4]完成绿化修剪车机械臂运动学分析，并利用ADAMS软件对绿化修剪车机械臂模型进行运动学仿真，该仿真分析结果为绿化修剪车的避障性能、最大作业速度以及避障时间提供理论依据。

1 绿化修剪车机械臂运动学建模

绿化修剪车机械臂是二自由度串联开式运动链[5]，其三维模型如图1所示。关于二自由度串联机构的运动学分析方法，一般有几何法和矩阵分析法等。几何法比较直观，适用于简单机构的运动学分析，而矩阵分析法适用于多矩阵运算和借助计算机求解的情况。考虑到绿化修剪车机械臂控制精度和后期便于借助计算机仿真，本文应用矩阵分析法建立绿化修剪车机械臂的运动学模型[6]。

图1 绿化修剪车避障工作装置的三维模型

为了便于矩阵法分析，本文对绿化修剪车机械臂模型进行了简化，简化后的运动矢量关系如图2所示。图中XO4Y为直角坐标系，O4为大臂与小臂的铰接点。O3为运动轨迹上的虚拟点，A为旋转油缸与大臂的铰接点，B为小臂与旋转油缸的铰接点，C为小臂与割草头旋转油缸的铰接点，D为割草头与割草头油缸活塞杆的铰接点，E为小臂与割草头的铰接点，Lj(j=1,…,13)为机构的矢量杆，θi(i=j,…,13)为矢量杆的方位角。

图2 绿化修剪车机械臂运动矢量示意

通过求解各矢量杆的长度和方位角，最终确定绿化修剪车割草机的运动轨迹、速度、加速度，以及各关节的角速度、角加速度。

以矢量杆L2的长度作为已知量，进行绿化修剪车机械臂运动学分析。由图2所示矢量杆及方位角，构建矢量三角形O4AB，可获得矢量方程

(1)

将机构的矢量方程分别投影在x、y轴上，并写成标准方程形式，可得

(2)

将式(1)对时间求导可得

(5)

求解式(5)，即可求得角加速度ω2、ω3。式(5)的矩阵形式为

(6)

将式(6)对时间二次求导，可得

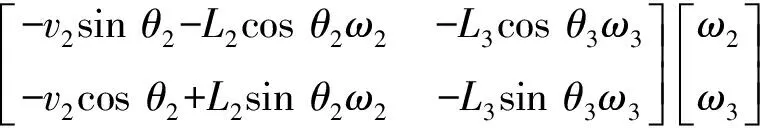
(7)

求解式(7)即可获得角加速度α2、α3。

HIV需借助易感细胞表面的受体进入细胞，包括第一受体（CD4，主要受体）和第二受体（CCR5或CXCR4等辅助受体）。根据HIV对辅助受体利用的特性将HIV分为X4和R5毒株。R5型病毒通常只利用CCR5受体，而X4型病毒常常同时利用CXCR4、CCR5和CCR3受体。值得注意的是，在疾病的早期阶段HIV常利用CCR5作为辅助受体，而在疾病进程晚期时病毒常利用CXCR4作为辅助受体。

根据图2中各矢量的关系，构建矢量三角形O4EC，即可得到

L5sinθ5+L10sinθ10=L7sinθ7

(8)

解式(8)，即可求得θ10表达式

(9)

在图2中构建矢量多边形O4EFO3，可建立矢量位置方程

(10)

将式(10)在x、y坐标轴上投影，可得

(11)

求解式(11)，即求得L12、θ11的表达式

(12)

(13)

在式(12)中，中间变量Ic=2L7cos(θ12-θ7)-2L13cos(θ12-θ13) ，将式(11)分别对时间求一次导数和二次导数，可得v12、a12、ω11、α11。

在图2中构建矢量多边形O4CDE，可建立位置方程

(14)

同理，将式(14)在x、y坐标轴上投影，可得

(15)

求解式(15)，即可求得L6、θ6的表达式

(16)

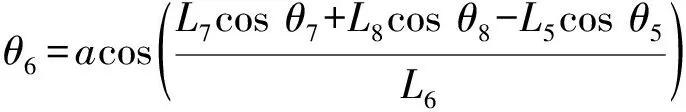
(17)

将式(15)分别对时间求一次导数和二次导数，即可得v6、a6、ω6、α6。

通过式(1)～ (17)可完成绿化修剪车机械臂的运动学分析和计算，在分析和计算前需要给定运动方程，即给出与机构自由度数目相等数量的运动方程[7]。结合绿化修剪车臂架旋转油缸运动规律(L2、v2)和割草机旋转油缸运动规律(L6、v6)，给出对应的驱动方程，分别如图3、4所示。其中0～2.50 s内工作臂向非障碍物侧运动，2.50～4.77 s内工作臂复位。

图3 臂架旋转油缸运动参数

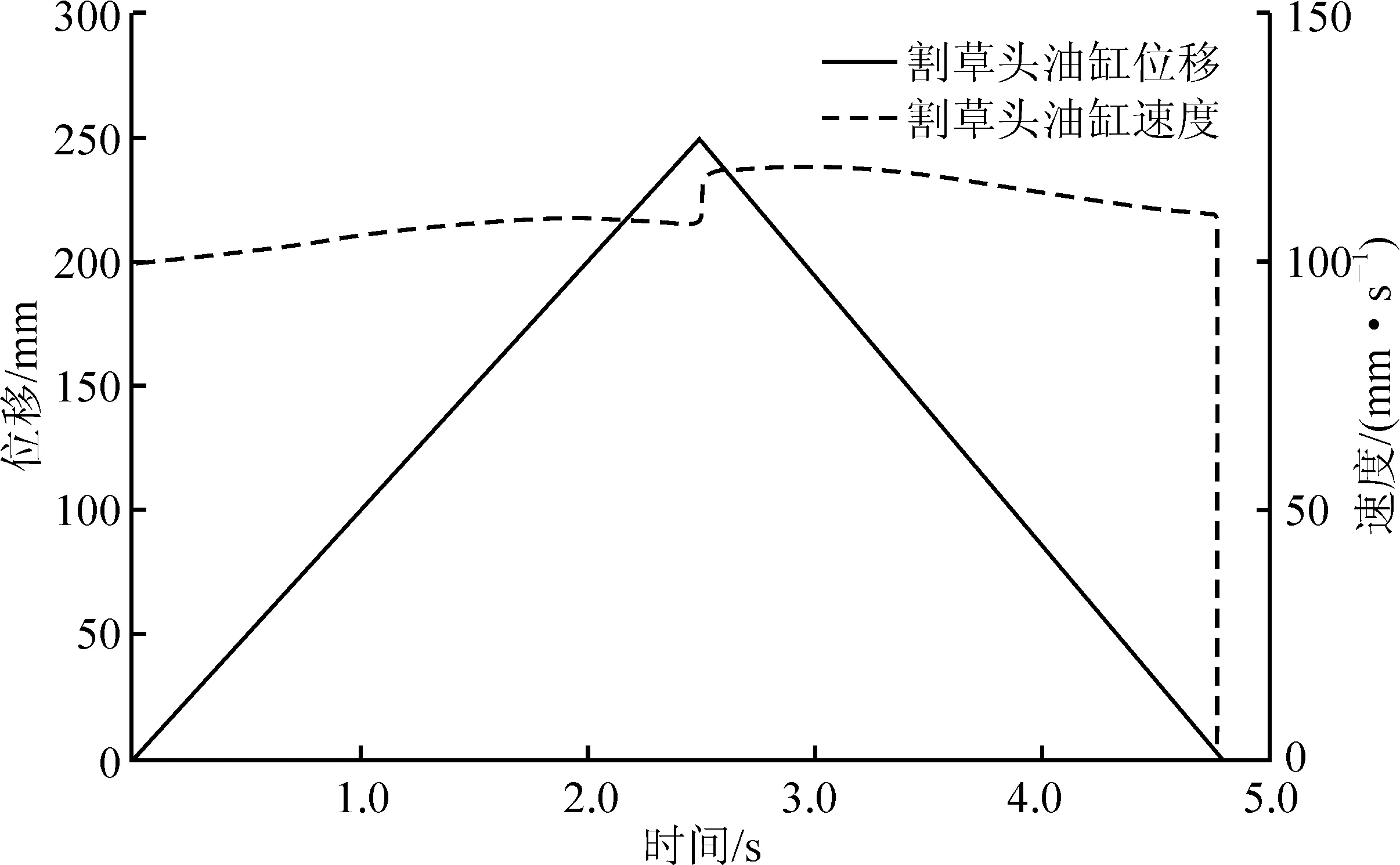
图4 割草头回旋油缸运动参数

2 工作臂运动学分析

绿化修剪车机械臂末端割草机的运动轨迹、速度和加速度，决定了绿化修剪车机械臂的稳定性、工作效率以及能否有效地避开障碍物，也是绿化修剪车作业速度和避障液压系统设计的重要依据。本文应用ADAMS软件进行仿真[8]，获得割草机触杆末端运动包络图(割草头末端F点的运动轨迹)，如图5所示。

图5 割草头触杆末端运动包络

由图5可知，在给定运动参数下，割草头末端触杆运动轨迹为外圆弧[9]，外圆弧形运动轨迹提高了绿化修剪车机械臂避障的灵活性[10]。由绿化修剪车运动包络图可知：绿化修剪车在x、-y方向存在位移；x方向的位移能够保证割草机顺利地避开障碍物，-y方向的位移能够避免割草机触杆与障碍物过度挤压碰撞。

以各关节z轴为旋转轴，可确定关节点1、关节点2的角位移、角速度和角加速度曲线，如图6～8所示。

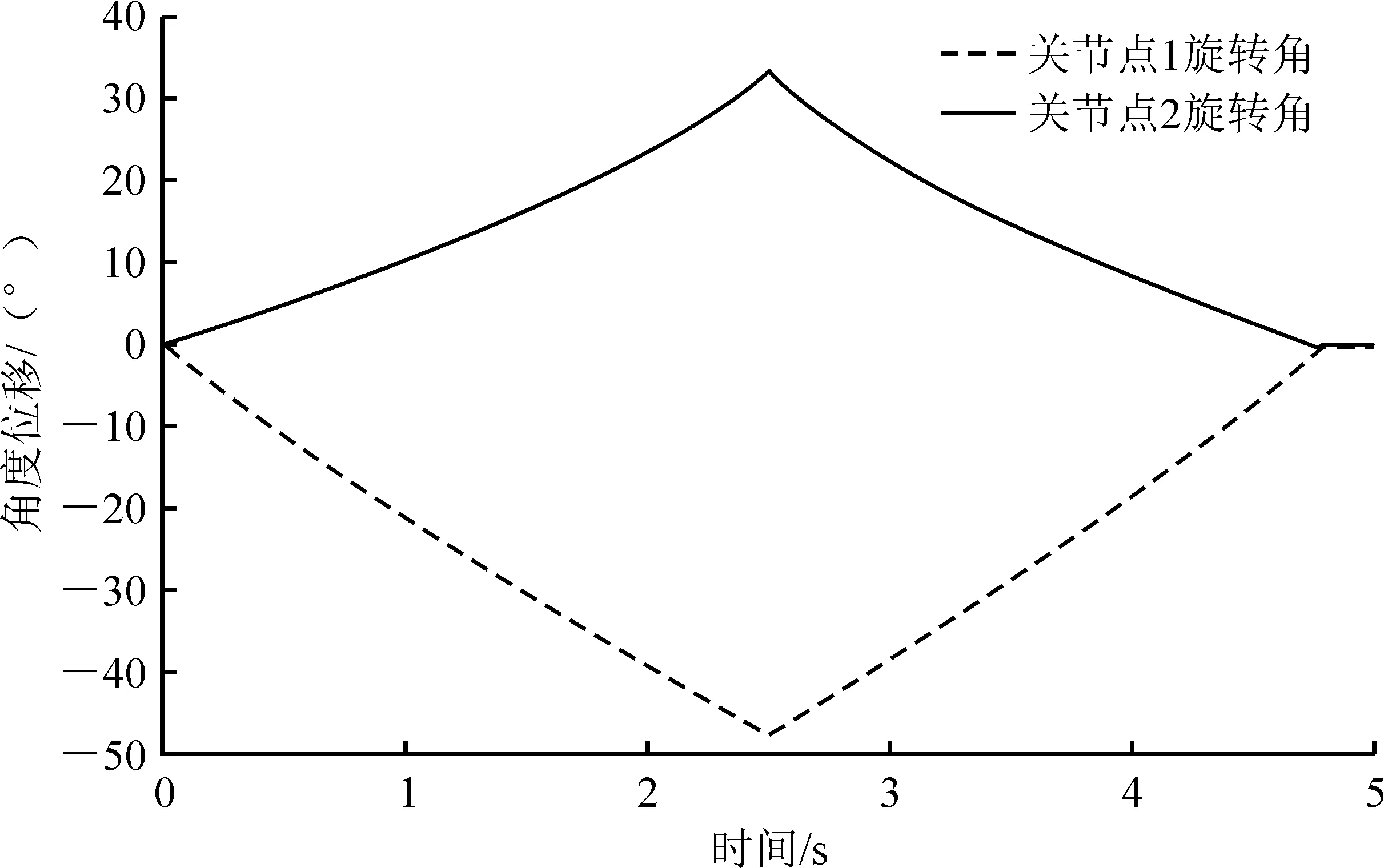
图6 关节点角位移

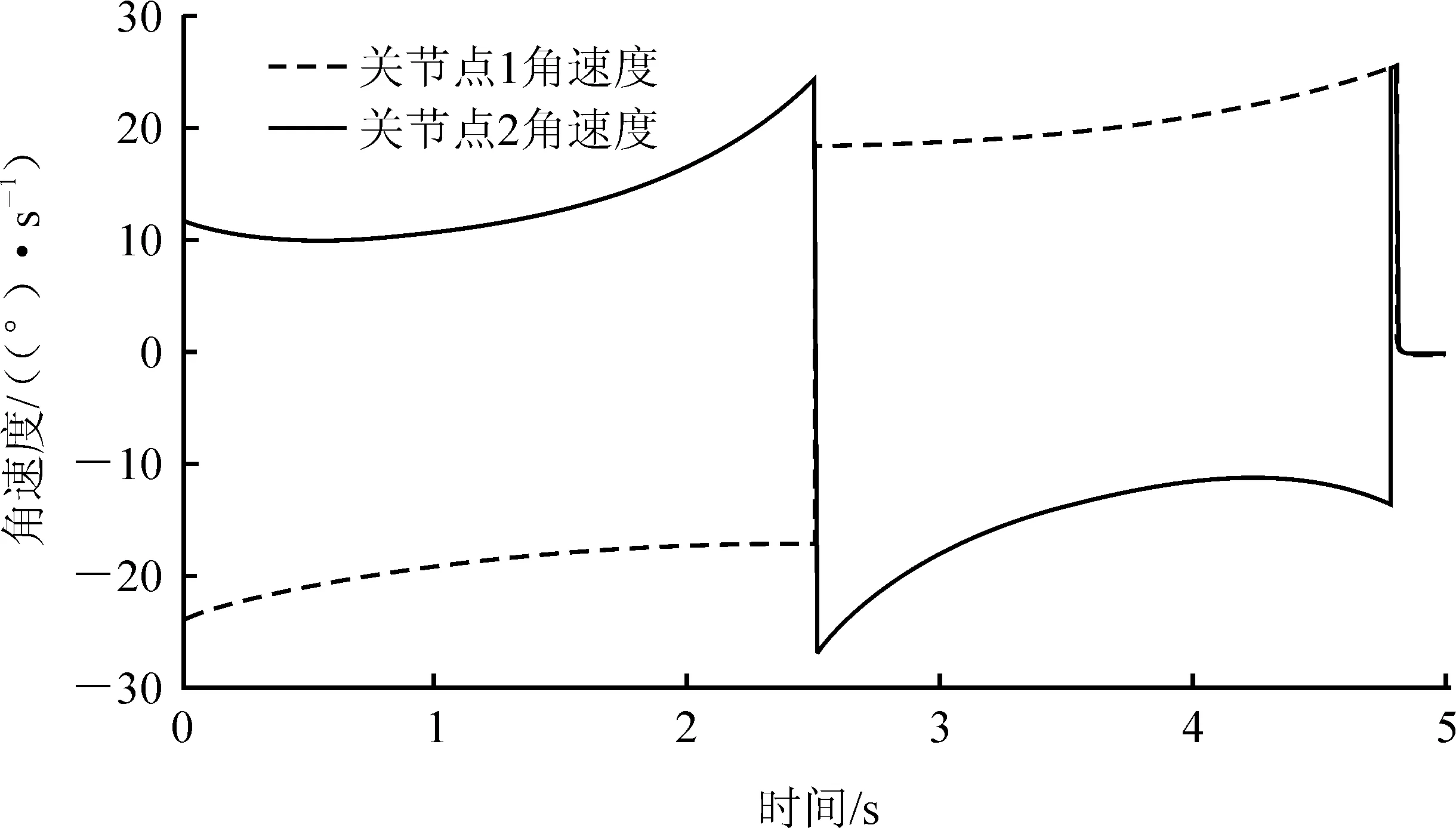
图7 关节点角速度

图8 关节点角加速度

由关节1、关节2的运动曲线可以看出，各连杆机构没有运动错位和运动死点，曲线平滑，表明机械结构设计合理，满足绿化修剪车避障的运动学要求[11]。由仿真结果可知，完成一次避障，关节点1角位移为0～-45°,角速度为-17.5 (°)·s-1；关节点2角位移为0～35°,角速度为13.5 (°)·s-1。

以割草机触杆右端点为标记点，通过仿真，可确定触杆在x、y方向的位移、速度和加速度曲线，如图9～11所示。

图9 割草机触杆末端位移曲线

图10 割草机触杆末端速度

图11 割草机触杆末端加速度

由仿真结果可知，在工作臂避障和复位过程中，割草机触杆末端的位移、速度和加速度曲线平稳、光滑、无折断点，满足运动学要求。当完成一个避障动作时，触杆末端在x方向位移变化量为877.5 mm，y方向位移变化量为1 337.5 mm；当割草头向非障碍物侧旋转时，在2.5 s内，x方向的速度从0增加至725 mm·s-1，加速度为250 mm·s-2，y方向速度从720 mm·s-1减小到500 mm·s-1，加速度为-150 mm·s-2；当工作臂复位时，割草机触杆末端的速度和加速变化情况与避障时相反。由于仿真过程中未忽略机械臂的转动惯量，故机械臂在运动停止时出现冲击现象。

将绿化修剪车的位移进行矢量分解，可求得避障时绿化修剪车的最大作业速度为1.5 km·h-1，完全避开障碍物需要2.18 s。

3 结 语

通过理论分析和运动学仿真，可得出以下结论。

(1)建立了绿化修剪车机械臂的串联二自由度运动学模型，分析了机械臂运动过程。通过理论分析和仿真验证了该运动模型的正确性。

(2)在臂架旋转油缸和割草头旋转油缸的联动工况下，绿化修剪车割草机的运动轨迹为外圆弧。

(3)绿化修剪车机械臂各关节运动曲线表明，该结构设计合理，满足绿化修剪车对避障工作装置的运动学要求。

(4)通过ADAMS进行了运动学仿真，获得了绿化修剪车割草机触杆末端的运动参数，确定了绿化修剪车避开障碍物所需时间及避障时的最大作业速度，为动力系统和控制系统的设计奠定了基础。

本文仅从运动学角度对绿化修剪车机械臂进行分析，可进一步进行动力学及控制系统分析。