基于分子动力学原理的性质计算模拟

胡永波 聂德志

【摘 要】使用SCIGRESS软件，应用分子动力学方法，选择NPT系综，模拟从2200K降温到1000K的过程中各参数的变化情况，得到了的势能、密度、双体分布函数、均方位移、多面体和多边形随温度变化的计算结果。

【关键词】SCIGRESS;分子动力学;双体分布函数;扩散系数

一、分子动力学原理

分子动力学是在原子分子水平上求解多体问题的重要计算机模拟方法，可以预测纳米尺度上的材料动力学特征。通过求解所有粒子的运动方程，分子动力学方法可以用于模拟与原子运动路径相关的基本过程，在分子动力学中，粒子的行为是通过经典的牛顿运动方程，所描述的分子动力学是确定性方法，一旦出使构型和速度确定了，分子随时间产生的运动轨迹也就确定了。分子动力学的标准流程如下：

1.Initialize——初始化粒子的空间位置和速度

Boltemann能量均分定理：对于处在温度为T的平衡状态的经典系统，粒子能量中每一个平方项的平均值等于kBT/2，下列公式表达了微观系统总动能和宏观温度的关系：

2.Forces——计算粒子的受力

在保守力场中，保守力等于势能函数的梯度，即：

其中，U1表示外力场或边界条件（如容器壁）;U2表示两体作用势，一对原子之间的作用力，不包含其他原子的影响;U3表示三体作用势，描述由于第三个原子的存在对原子对之间作用力的影响。

在具体问题当中，需要选取合适的势函数以及周期性边界条件来通过有限的模拟区间，得到具有宏观尺寸的结构材料的特性。

3.Motion——使用牛顿运动方程得到系统随时间的演进

在该情形下，需假设粒子受力不变且粒子运动符合牛顿运动方程。根据Verlet算法原理，粒子位置的Taylor展开式如下：

据此求解运动方程，求解得到系统的粒子位置、速度、加速度随时间的演进。这一步驟的实现可以依赖于多种成熟的算法。除此之外，还可使用Leap-frog算法、Velocity Verlet算法等。

4.Analysis——计算系统的密度、温度、势能等参数

在本次实验中，除了势能、温度之外，我们还得到了双体分布函数及多面体、多边形的结果。

5.Summarize——对计算数据进行整理分析

根据得到的数据对演化过程的物理学意义进行分析。

二、模拟计算步骤

1.选取区域大小（5*5*5）、晶体结构、NPT系综、步长、温度梯度（2200-1000k），确定势函数

2.设定初始条件，原子分子初始速度服从波尔兹曼随机分布

3.求解运动方程，等待系统达到平衡态，输出稳定的参数值

4.用时间平均代替系综平均，对宏观物理量进行统计

三、计算结果和分析

3.1 体系的T温度、D密度、P势能随步长的变化情况

定性分析程序的运行结果，该体系在温度从2200K达到1000K的过程中，密度随时间不断增大。势能随时间逐渐减小。说明体系性质正在由液体逐步趋近于固体。

密度是金属的一个重要的热物理性质，对于理解液-固相转变、凝固过程、传质、热对流，探索液态结构和亚稳态相变等有一定意义。为了更加清晰的表示密度的变化情况进行了缩放操作，实验所获得的密度逐渐增长。

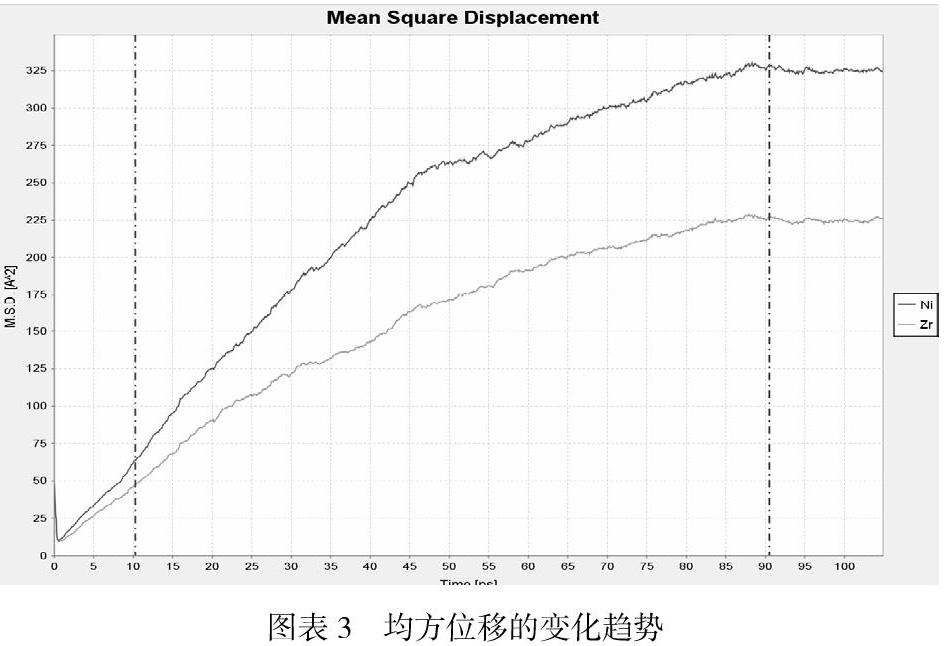
3.2 、均方位移变化趋势

程序运行得出镍和锆的均方位移变化趋势如上图所示。通过分段读数，显示Plot Information，读到扩散系数：

以上表格所列出的是和在不同温度下的扩散系数以及整个系统演变过程中的扩散系数。结果表明扩散系数逐步降低。这是由于温度的降低减缓了扩散的发生。

3.3计算所得的双体分布函数

实验得到了计算所得的2200K，2000K，1800K，1600K，1400K，1200K下、、和总体系的双体分布函数，以1600K的为例，结果如下：

根据以上数据，绘制、和总体系的双体分布函数第一峰的峰值变化图。结果表明，随着温度的降低双体分布函数第一峰、第二峰的峰值在不断上升。

双体分布函数显示，液态金属的结构介于固体和液体之间，兼具短程有序和长程无序的特征。原子可以在确定的范围内运动，因此双体分布函数在短距离有类似于固体的峰，峰的宽化由原子运动引起。在长距离时，双体分布函数的值趋近于1，表明在长程范围内液态金属具有气体的特征，原子的分布完全无序。

3.4多面体、多边形结果

选取了三个代表点，展示了演化初期（液态）、中期、后期（固态）的多面体结果和多边形结果：

结果表明，大多数多面体的数量随时间未发生明显变化，主要是四面体和六面体的数量变化较大。其中，四面体逐渐增多，六面体先减少，后增多。变化原因主要是固体和液体的微观结构不同。

大多数种类多边形的数量随时间未发生明显变化，存在量最大的是四边形、三边形次之，接下来是五边形，最少的始终是六边形。变化原因主要是固体和液体的微观结构不同。

四、总结

随着降温过程的进行，液态金属由液体变为固体。温度越低，体积越小，密度越大，扩散系数也逐步降低。双体分布函数计算结果显示，第一峰的峰值不断上升。最后计算并分析了液态金属的多面体、多边形结果，体系中多面体和多边形请款随温度无明显变化。

参考文献：

[1]王海鹏.液态金属结构与性质.西北工业大学.2020.8.

[2]刘金远，段萍，鄂鹏.计算物理学.科学出版社.2016.

[3]武玉琴.金属凝固过程中过渡态现象研究.山东大学.2008.

作者简介：

胡永波，男，2000，陕西渭南，主要研究材料及物理，西北工业大学物理科学与技术学院，西安，中国陕西省西安市长安区东祥路一号西北工业大学长安校区。

聂德志，男，2000，江苏盐城，主要研究能量采集及微机电系统，西安，中国西北工业大学长安校区。

（作者单位：西北工业大学）