新型铝包覆碳纤维导线力学性能分析研究

董 罡，魏 桐

（1.国网山东省电力公司，山东 济南 250001；2.天津大学机械工程学院，天津 300350）

0 引言

随着城市化水平与经济水平的不断发展，社会用电需求日益提高。输电容量的提升主要有两种途径：一是增大输电电压，二是增大输电电流［1-3］。为安全可靠地提高输电能力，许多研究者不断研制性能优于传统钢芯铝绞线的架空输电线路用导线。

刘燕［4］针对新型耐热铝合金导线的力学特性进行了研究，证明该导线性能优于普通铝合金导线，并尝试提出一种导线安全评定方法。吴庆美［5］采用实验方法对铜包钢双金属复合导线的电学和机械性能进行了探究，并对制备工艺与影响规律开展了分析。随着技术水平的不断发展以及研究工作的持续深入，人们开始使用有机复合材料代替金属制造导线芯棒。其中，碳纤维复合芯导线因其强度大、重量轻、耐热性高和耐腐蚀性能好等优点，逐渐被人们关注和研究［6］。黄礼平等人［7］对某种碳纤维导线的耐热、载流以及机械性能开展了相关试验工作，并对不同季节工况下的运行特性进行了分析。刘辉等人［8］对碳纤维复合芯材料设计选型以及成型工艺等技术进行了论述，验证了导线结构设计的合理性。李斌等人［9］通过真型耐张塔试验平台对比探究了碳纤维复合芯导线和多种传统导线的弧垂特性。为解决传统碳纤维复合芯导线存在的耐压性能差以及易折断等实际问题［10］，董罡［11］论述了一种采用铝包覆工艺制造的新型碳纤维复合芯导线，并通过实验方法对多种特性进行了探究，结果表明该新型碳纤维导线具有良好的性能。上述文献虽然初步研究了各类新型导线具有的优势，也尝试采用新型结构提高碳纤维导线的机械性能，但均没有涉及不同受力情况下铝包覆新型碳纤维复合芯导线局部结构的力学特性。

基于JLRX1／F2A－800／70 铝包覆新型碳纤维复合芯导线进行研究，通过建立该型号复合芯导线以及传统碳纤维导线的三维物理模型，采用有限元分析方法开展数值模拟计算，对比分析两种导线在受到径向压力或轴向拉力作用下的抗压与抗拉性能，为新型碳纤维复合芯导线的制造、安装及运行提供基础。

1 数值方法及模型建立

1.1 数值计算方法

应用以有限元方法为基础的静力学计算平台进行数值模拟计算。有限元方法是基于近代计算机快速发展而成熟起来的一种近似数值方法，可以用来解决力学和数学中带有特定边界条件的偏微分方程问题。该方法的基本求解思想是将计算域划分为有限多个互不重叠的单元，在每个单元内，选择一些合适节点作为求解函数的插值点，借助变分原理或加权余量法，将微分方程离散并进行求解计算［12-13］。

1.2 模型建立

传统碳纤维复合芯导线自内而外由碳纤维芯棒、内层铝绞线与外层铝绞线构成。而文献［11］中所提及的铝包覆新型碳纤维导线由碳纤维复合芯棒、铝包覆结构与外层铝绞线组成。两种导线的实际结构如图1—图2 所示。两种导线的主要区别在于，铝包覆新型碳纤维导线将传统导线的内层铝绞线通过特殊工艺替换为无缝铝包覆结构。

图1 传统碳纤维复合芯导线

图2 新型碳纤维复合芯导线

参照JLRX1／F2A－800／70 铝包覆新型碳纤维导线的结构尺寸以及Q／GDW 1851—2012 《碳纤维复合材料芯架空导线》中的相关参数［14］，分别对两种碳纤维复合芯导线进行三维建模，具体模型尺寸以及各部分材料的物理参数如表1—表2 所示，两种导线的三维计算模型如图3—图4 所示。

表1 两种导线结构参数

表2 模型各部分的材料参数

图3 传统碳纤维复合芯导线计算模型

图4 新型碳纤维复合芯导线计算模型

2 碳纤维复合芯导线力学性能分析

2.1 抗压性能对比分析

为对比两种导线的抗压能力，将两种模型的一端设定为固定端约束条件，即限制各方向上的位移和旋转。同时，在两种导线的另一端施加大小为30 N、方向为垂直向下的作用力，以此研究导线在过滑轮等实际工作条件下受到近似弯折外力时的力学特性。基于上述模型与边界条件，通过静力学计算平台开展数值模拟。计算结束后，对比分析模型中导线碳芯表面应力和总形变的数据结果，应力分布云图如图5—图6 所示。

图5 传统导线碳芯径向受压的应力分布

图6 新型导线碳芯径向受压的应力分布

图5 与图6 中，左端为固定端，右端施加了垂直向下的作用力。对比两图可知，传统导线碳棒表面的最大应力值约为5.08 MPa，而新型导线碳芯表面的最大应力值约为0.96 MPa，相较之下，后者应力下降了约81%，说明采用了铝包覆结构的导线在较大程度上降低了碳芯的最大应力。从应力分布上来看，传统导线芯棒存在较大的应力梯度，且较为密集。在实际生产及施工过程中，这种应力分布状况容易造成芯棒的损伤甚至发生断裂。而新型导线芯棒的应力分布较为均匀且没有产生明显的应力集中现象。综合考虑应力大小的结果，说明新型碳纤维导线能够有效降低芯棒折断的可能性，从而减小实际工程应用中事故发生的概率。

为进一步对比两种导线的力学特性，对碳棒表面的总形变分布进行分析，分析结果如图7 所示。此外，为了更加直观体现总形变的分布规律，分别统计沿两种导线轴向不同位置处的总形变数值并绘制曲线进行对比研究，结果如图8 所示。

由图7 可知，两种碳纤维复合芯导线的总形变分布基本一致，具体表现为左侧固定端基本为零，沿轴向慢慢增大，到模型右侧受力端达到最大值。由图8 可以得到传统导线碳芯的最大形变约为0.258 mm，新型导线碳芯的最大形变约为0.289 mm，二者相差不多，说明两者在径向受压的工况下形变特性基本相同。同时，该形变结果与碳芯长度相比量级很小，在一定程度上可以忽略其对导线整体力学性能的影响。

图7 两种导线碳芯径向受压的总形变分布

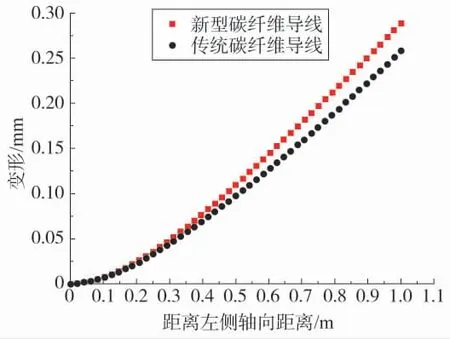
图8 径向受压时碳芯形变沿轴向分布曲线

此外，为了对比不同导线在运行过程中抗拉性能的差异，针对上述建立的三维导线模型，基于本文所提计算方法，对两种导线开展承受轴向拉力的数值模拟与分析。

2.2 抗拉性能对比分析

根据Q／GDW 1851—2012 《碳纤维复合材料芯架空导线》 中关于型线同心绞碳纤维导线额定拉断力的理论和计算方法［14］，拉断力计算公式为

式中：f 为导线的额定拉断力；f1为碳纤维材料芯的拉断力，由复合材料芯标称面积与碳纤维最小抗拉强度的乘积确定；f2为铝部分的拉断力，由导线铝标称面积与铝单线最小抗拉强度的乘积得到。通过式（1）可以计算出对于抗拉性能研究所采用的拉断力大小约为240 kN，并将该数值作为本工况下的计算边界条件。

将两种碳纤维复合芯导线模型的左端设定为固定端边界条件，在两类导线模型的右端施加大小为240 kN 的轴向作用力，从而模拟导线受到拉力的工况。基于上述的三维计算模型与边界条件，通过有限元计算平台开展数值模拟，并对两种导线的抗拉性能进行对比与分析。分析得出两种导线碳芯受轴向拉力作用下的应力分布云图如图9—图10 所示。

图9 传统导线碳芯受拉力的应力分布

图10 新型导线碳芯受拉力的应力分布

对比图9 与图10 中导线受轴向拉力作用下的应力大小可知，传统碳纤维导线芯棒表面的最大应力值约为1.79×104MPa，新型碳纤维导线芯棒的最大应力值约为1.49×104MPa，后者相较于前者下降了约17%。而从应力分布来看，传统导线碳棒表面的应力呈现近似条带状的分布特征，说明有较明显的应力集中发生。然而，新型导线碳芯表面上的应力梯度变化较小，应力分布较为均匀。综合考虑该工况下应力大小与分布特性，结果充分说明新型碳纤维导线在受拉力作用下的力学性能优于传统导线。

进一步的对比考察两种导线的总形变特征，分布如图11 所示。与上文类似，分别统计沿两种导线轴向方向上不同位置处的总形变数值，并绘制曲线开展对比分析，如图12 所示。

图11 两类导线碳芯受拉的总形变分布

图12 轴向受拉时碳芯形变沿轴向分布曲线

由图11 可以看出两种导线的总形变分布基本相同，均为从左端沿导线轴向缓慢增长并在模型右侧达到最大值。同时，由图12 可知传统导线碳芯的最大总形变约为0.133 m，新型导线碳芯的最大总形变约为0.114 m，相比之下后者减小了约14%，表明铝包覆结构新型碳纤维复合芯导线可以有效降低碳芯受轴向拉力作用下所产生的形变，也说明铝包覆结构能够更好保护碳棒的完整性，进而提升导线的整体力学性能。

3 结语

基于JLRX1／F2A－800／70 铝包覆新型碳纤维导线与传统碳纤维导线进行研究，通过分别建立两种导线的三维物理模型，采用有限元分析方法开展数值模拟计算，对比分析了两者在受到径向压力以及轴向拉力作用下的力学性能。

当固定两种导线的一端并在另一端施加相同的径向压力时，铝包覆新型碳纤维复合芯导线的最大应力值明显小于传统导线，应力梯度变化也较小，分布更加均匀。同时，两者的总形变基本一致，说明新型碳纤维导线的抗压性能优于传统碳纤维导线。

当固定两种导线的一端并在另一端施加相同的轴向拉力时，铝包覆新型碳纤维复合芯导线的最大应力值和总形变均小于传统碳纤维导线。同时，前者应力分布更为均匀，少有应力集中现象发生，说明新型碳纤维导线的抗拉性能优于传统碳纤维导线。

不同工况下新型碳纤维导线的力学性能均优于传统碳纤维导线，说明在一定程度上新型导线能够解决实际施工和运行过程中碳纤维导线存在的问题与隐患。