基于城市居民峰谷电价响应特性的超短期负荷预测研究
林启开,王 珂,陈文学,盛兆乐
(1.国网山东省电力公司检修公司,山东 济南 250118;2.中国电力科学研究院南京分院,江苏 南京 210003)
0 引言
居民用电负荷具有柔性负荷的许多特征[1-2],近年来,通过电价机制引导柔性负荷[2-4]参与调度运行作为短时间尺度上的调度资源受到极大重视。峰谷电价的实施改变了居民用电特性,相应地,会增大负荷预测的难度,当前对电价变化后的负荷预测往往没有考虑峰谷电价转变带来的影响[5],在电价拐点处的负荷预测精度相对较低。基于此,采用电价变化点负荷增长率指标分析城市居民峰谷电价响应特性,用负荷增长率修正预测模型来考虑峰谷电价对电价变化点超短期负荷预测的影响。
1 城市居民峰谷电价响应特性分析
1.1 负荷增长率指标及其计算方法
以某市居民历史负荷数据分析,该市居民08∶00—21∶00 为峰电价,21∶00—次日08∶00 为谷电价。以电价变化点负荷增长率来描述城市居民峰谷电价响应特性,定义如式(1)所示。

式中:γ 为电价变化点负荷增长率;t 为电价变化时刻;lt为电价变化点的负荷值;Δt 为电价变化后的响应时间;lt+Δt为电价变化Δt 时间后的负荷值。
为简化分析,选取电价变化后3 个点的负荷增长率来分析居民峰谷电价的响应特性,分别取10 min、30 min 及30 min 内最值(最大或最小)负荷增长率,08∶10 和08∶30 处的负荷增长率分别用γ10min1、γ30min1表示,30 min 内的最值用γm1表示,21∶10 和21∶30 处的负荷增长率分别用γ10min2和γ30min2表示,30 min 内的最值用γm2表示。
1.2 负荷增长率相关性分析
居民在电价变化后的负荷增长率受节假日类型和温度的影响较大,利用SPSS 数据分析软件对2 个电价变化点进行相关性分析可得表1 和表2。Pearson 相关系数值越大,相关性越强,N 表示样本数目,日类型分工作日和节假日2 种类型。
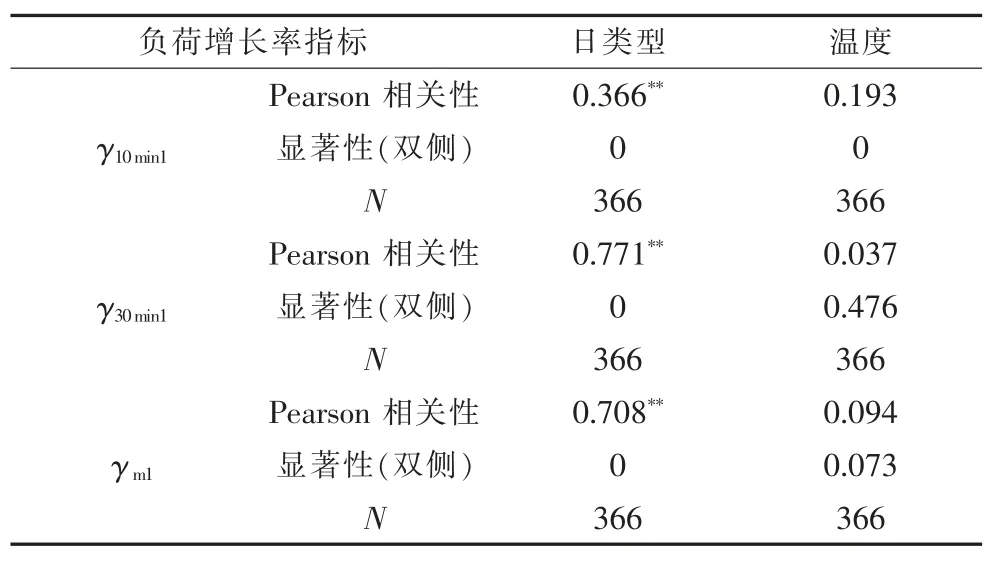
表1 08∶00 负荷增长率相关性
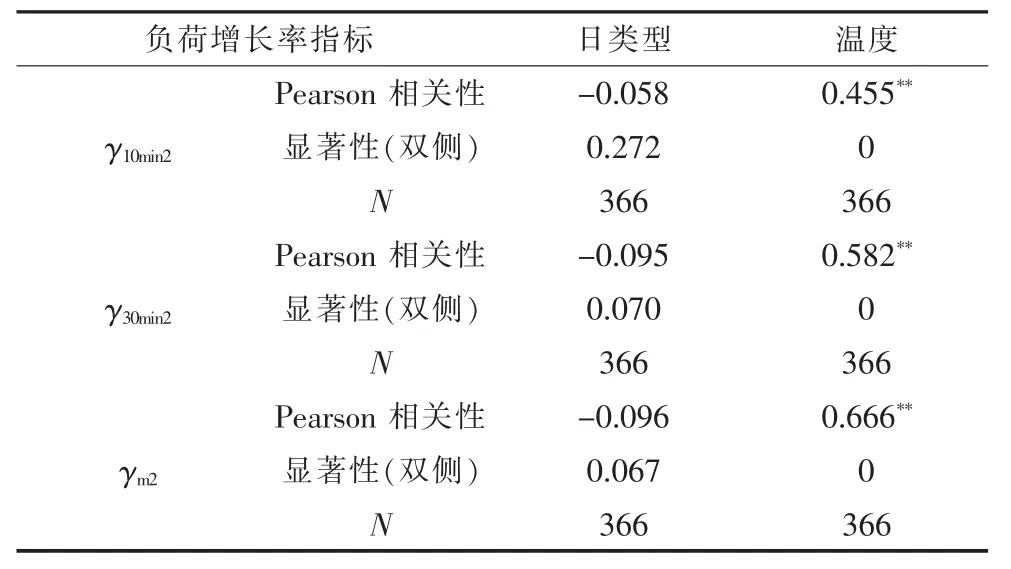
表2 21∶00 负荷增长率相关性
08∶00 处3 个负荷增长率与日类型相关系数分别为0.366、0.771、0.708,显著性检验值基本为零,在0.01 水平上呈现显著相关;负荷增长率与08∶00 温度相关系数均为超过0.2,相关性较弱。21∶00 处3 个负荷增长率与日类型相关系数绝对值均未超过0.1,负荷增长率与日类型基本不相关;负荷增长率与温度的相关系数分别为0.455、0.582、0.666,并且显著性的检验值基本为零,在0.01 水平上都呈现显著相关。
2 个电价变化点附近的负荷变化趋势如图1 所示。
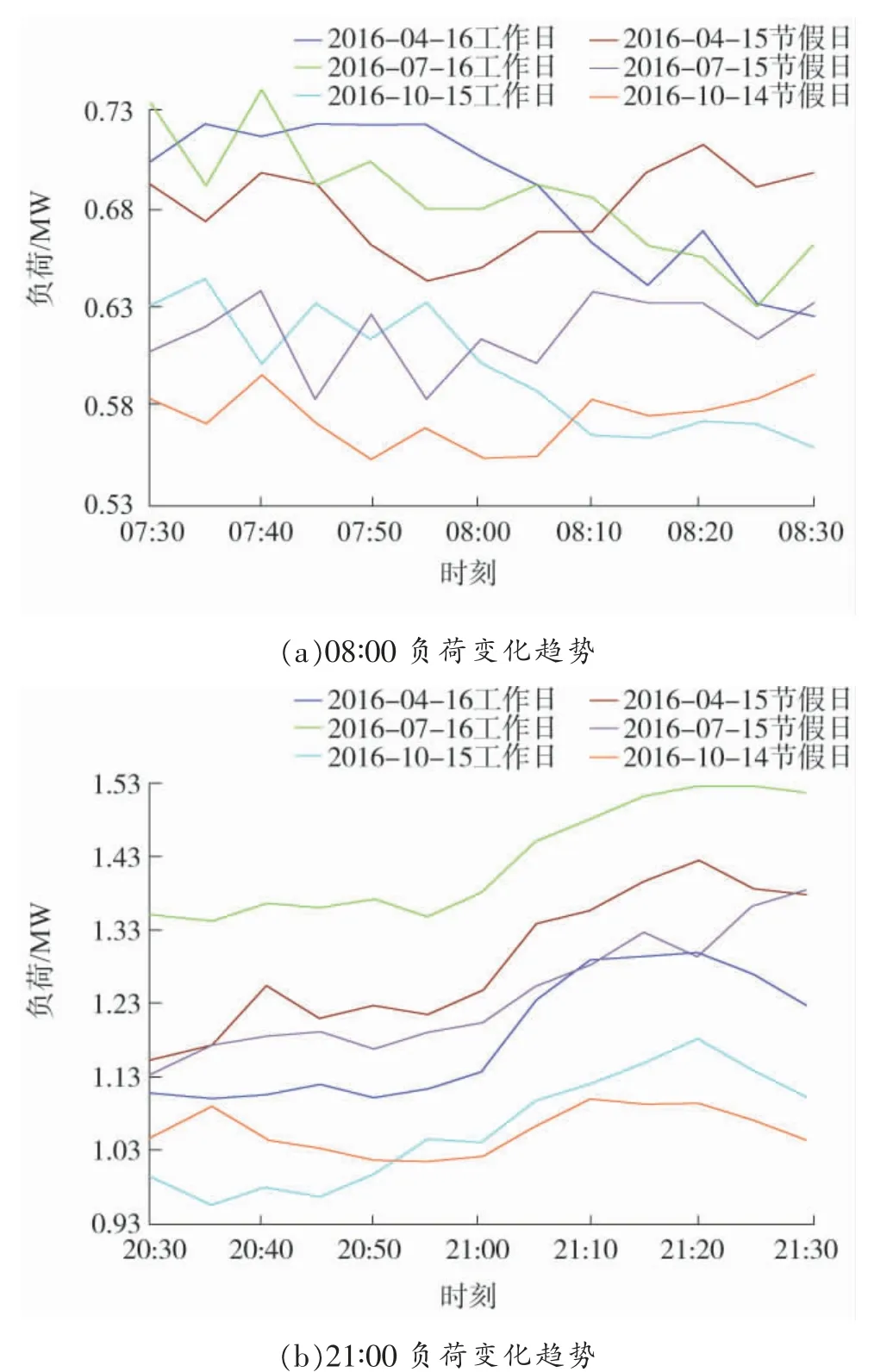
图1 电价变化点附近的负荷变化趋势
由图1(a)可知,居民负荷在由谷电价变为峰电价后并没有显著变化,电价升高没有减少居民负荷,且工作日与节假日负荷趋势不同。由图1(b)可知,居民负荷在21∶00 由峰电价变为谷电价以后出现一个明显的增长,且节假日和工作日都呈现增长趋势。这是因为一方面部分居民工作日在08∶00 需要外出上班,另一方面居民晚上电器使用较多,峰谷电价下可响应负荷较多,在电价变化后负荷变化比较明显。
2 居民负荷增长率时域特性分析
基于上文分析,居民峰谷电价在21∶00 由峰电价变为谷电价时起到的作用更加明显,所以分析21∶00负荷增长率特性更能体现峰谷电价的影响作用,具有明显的季节响应差异。
2.1 负荷增长率与响应时间的拟合模型
用MATLAB 拟合工具箱中拟合函数试探拟合分析,在用多项式模型进行拟合时可以达到较高的拟合优度,非常接近于1。用二次多项式模型拟合负荷增长率与响应时间的关系,模型可表示为
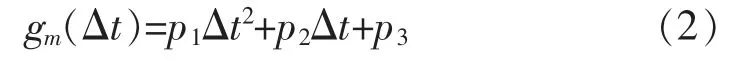
式中:m 为月份;Δt 为电价变化后响应时间;p1、p2、p3为随月份m 变化而变化的多项式系数。
随机选取某月为例求取拟合参数,并做出拟合曲线,某月负荷增长率多项式拟合曲线如图2 所示。
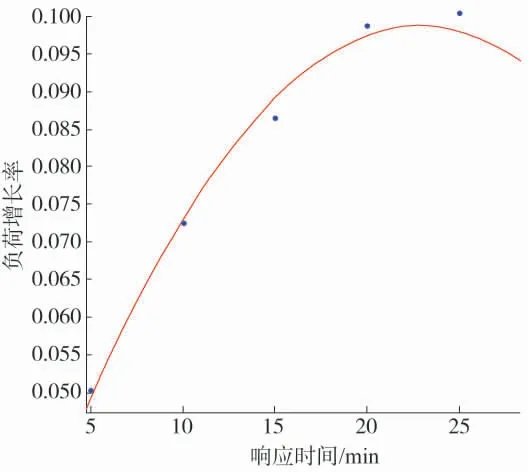
图2 某月负荷增长率多项式拟合曲线
由图2 可知,二次多项式模型对每个点的拟合误差都不大,且拟合优度和校正后的决定系数都非常接近于1,方差和均方根都接近于零。经验证,其他月份用二次多项式模型拟合时均可达到较高的拟合优度。
2.2 负荷增长率与月份的拟合模型
21∶00 负荷增长率变化具有很强的季节规律,上文分月对负荷增长率与响应时间进行了拟合,接下来分析相同响应时间尺度下负荷增长率与月份关系。以21∶05 负荷增长率拟合曲线为例分析,如图3所示,其中,纵坐标表示负荷增长率,横坐标表示月份,R2表示相关系数,越接近于1 说明拟合曲线越准确,自变量与因变量的关系越密切。
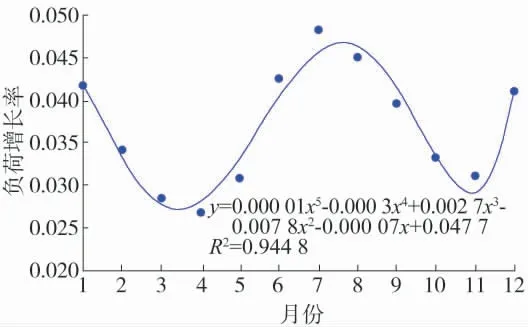
图3 21∶05 负荷增长率与月份拟合曲线
图3 为21∶05 负荷增长率与月份的拟合曲线,拟合曲线呈现两峰两谷,当用四次多项式拟合时,相关系数只有0.785 9,用五次多项式拟合时,拟合曲线表达式如图3 所示,相关系数达到0.944 8,可以很好地表示电价变化点5 min 负荷增长率与月份的关系。经分析,其他响应时间下也可以用五次多项式拟合负荷增长率与月份的关系,可以表示为
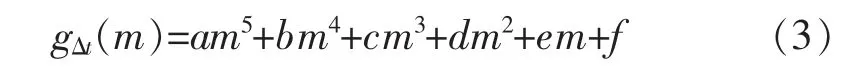
式中:a、b、c、d、e、f 为随Δt 变化而变化的多项式系数。
2.3 负荷增长率多元拟合模型
综合考虑负荷增长率与响应时间和月份的拟合模型,构建五次多元函数对月份尺度和响应时间尺度综合分析,构建的函数如式(4)所示。
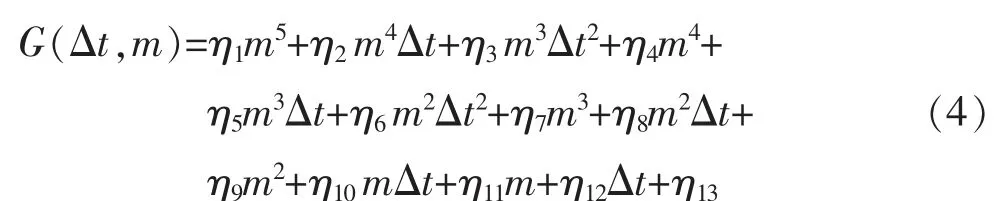
式中:G(Δt,m)为第m 月电价变化Δt 时间后的负荷增长率;ηi(i=1,2,...,13)为随m 和Δt 的变化而变化的多项式系数。
根据每月对应响应时间的负荷增长率,利用MATLAB 进行多元线性拟合得到拟合曲面如图4 所示。
拟合曲面呈现了负荷增长率与响应时间和月份之间的关系,7 月份和1 月份负荷增长率比其他月份大,且一般在电价变化后25min 出现最大值。为验证多元回归模型的准确性,计算负荷增长率残差分布如图5 所示。
在数理统计中,残差指实际观测值与回归拟合值的差,残差看作误差的观测值。利用残差所提供的信息,来考察模型假设的合理性及数据的可靠性称为残差分析。由图5 可知,只有2 个样本残差的置信区间没有包含零点,其他样本的残差置信区间都包含零点,说明回归模型能较好地符合原始数据。
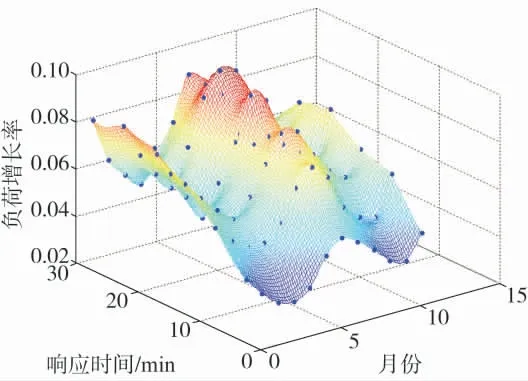
图4 负荷增长率多元回归函数辨识结果
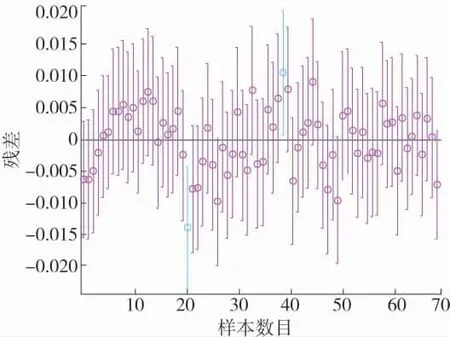
图5 负荷增长率多元回归残差分布
3 考虑负荷增长率修正的城市居民超短期负荷预测
采用人工神经网络[6-7]分别建立不考虑负荷增长率和考虑负荷增长率修正的预测模型,最后对仿真结果进行对比分析。
3.1 预测误差评价指标
在计算和分析误差指标时,有多种指标可以表示,在电力负荷预测计算分析中,常用来作为误差的评价指标有:
平均相对误差
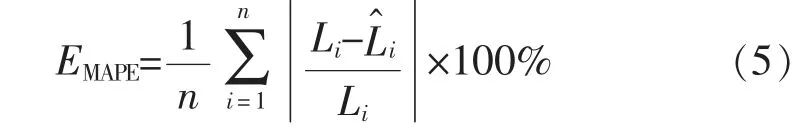
均方根相对误差
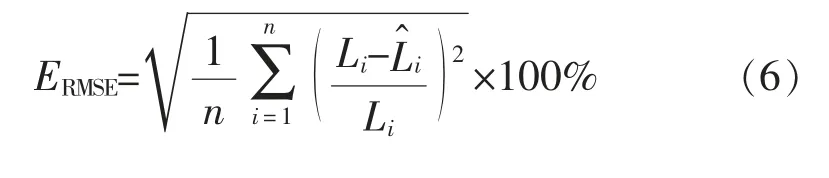
3.2 超短期负荷预测模型
使用单层隐含层的BP 网络分别建立不考虑负荷增长率和考虑负荷增长率修正的神经网络预测模型,如图6 和图7 所示。

图6 不考虑负荷增长率修正的预测模型
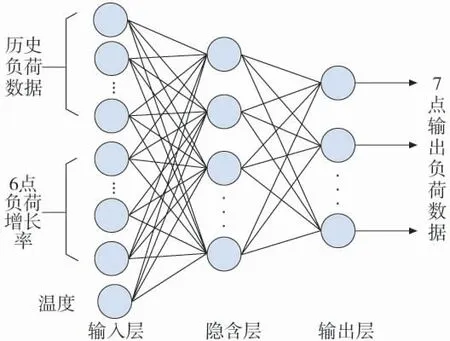
图7 考虑负荷增长率修正的预测模型
两种预测模型的目标输出都是电价变化点后30 min 内每5 min 负荷数据,共7 个负荷值(含电价变化点)。图6 模型取电价变化点前30 min 内每5 min负荷数据和前一天对应目标输出时刻负荷数据作为输入,共13 个负荷数据值。21∶00 城市居民负荷增长率与节假日类型相关性较小,所以不考虑节假日类型的影响,只需在仿真训练的时候剔除特殊节假日的影响即可,但与温度相关性显著,所以增加温度作为一个输入变量,因此输入节点数为14,输出节点数为7。图7 所示模型增加了对应月份电价变化后的负荷增长率(共6 个)作为输入量进行修正,这样输入层节点数就为20,输出节点数仍为7。
3.3 仿真分析
设置单层隐含层节点数为29,目标误差0.001,学习速率0.05,最大迭代次数1 000,对不考虑负荷增长率的网络模型训练,得到预测输出如图8 所示。设置隐含层节点数改为41,其他参数均不改变,用考虑负荷增长率修正的网络进行训练,预测输出结果如图9 所示。
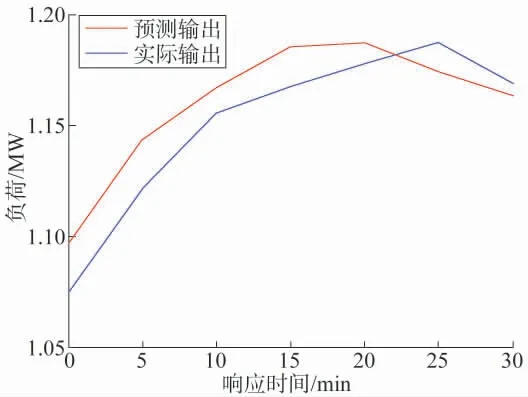
图8 不考虑负荷增长率修正的预测输出
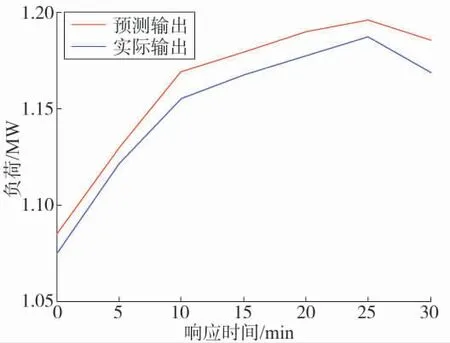
图9 考虑负荷增长率修正的预测输出
分析两种预测输出,考虑负荷增长率修正的预测输出负荷变化趋势与实际负荷变化趋势一致,而不考虑负荷增长率的预测输出在电价变化25 min 后出现与实际变化相反的趋势。对比两种模型的预测误差如表1 所示。

表1 两种模型预测误差对比 %
考虑负荷增长率修正的预测模型平均相对误差和均方根相对误差均小于不考虑负荷增长率修正得出的结果。通过电价变化点负荷增长率对负荷预测模型进行修正,可提高电价变化后超短期负荷预测的精度。
4 结语
通过对城市居民峰谷电价响应特性进行分析,发现日间电价变化点负荷增长率受节假日类型影响较大,与温度基本无关;夜间电价变化点负荷增长率受温度影响较大,与节假日类型基本无关。居民在夜间电价变化点做出的响应比日间电价变化点的响应敏感。
通过对居民负荷增长率时域特性进行分析,发现居民响应峰谷电价有明显季节规律。电价变化后夏冬季负荷增长率比春秋季大,夏季比冬季略大。夏冬季峰谷电量比春秋季节小,为居民降温取暖负荷响应峰谷电价所致。不同月份居民负荷增长率与响应时间符合二次多项式关系,不同响应时间尺度下居民负荷增长率与月份符合五次多项式关系。
利用人工神经网络建立超短期负荷预测模型,预测结果表明用电价变化点负荷增长率修正峰谷电价可以提高电价变化后超短期负荷预测的精度。

