附加基线矢量约束的双站协同精密定位方法

陈万通, 尚正辉, 汪竹青

(中国民航大学 天津市智能信号与图像处理重点实验室,天津 300300)

0 引 言

近年来全球卫星导航系统(GNSS)精密单点定位(PPP)技术越来越受到GNSS领域的广泛关注. PPP利用测码伪距和载波相位观测值以及国际GNSS服务(IGS)提供的高精度的卫星星历和卫星钟差产品,同时应用精化的误差模型和误差改正产品改正定位过程中的多种误差,进而实现国际地球参考框架下的高精度单点定位[1]. PPP相比于传统的单点定位和实时动态(RTK)定位方式,具有定位精度高,不受相对定位作用范围限制,操作方便,成本低廉等优点. 由于上述优点,PPP具有广泛的工程应用价值,现已全面应用到工程测绘、交通、大气水汽反演、精密授时等多个领域.

PPP通常采用Kalman滤波进行位置及其他参数的解算. Kalman滤波进行参数解算时不仅要包含必要的观测模型,同时引入了动态模型. 因此,Kalman滤波的精度不仅取决于观测值的精度,还依赖于建立的动态模型和给定的初值是否准确. 然而,由于接收机运动状态具有很多的随机不确定性,很难通过精确建模来描述,初始信息也很难精确获取,这给Kalman滤波递推计算带来了一定困难,不仅可能降低精度,滤波甚至可能会发散. 改善Kalman滤波的性能通常从建立更准确的动态模型和采用特殊的外部先验信息入手. 许多学者提出了抗差滤波[2]、自适应选权滤波[3]等改进模型来控制观测异常和动态模型误差的影响,另外,国内外学者对于带约束的滤波算法进行了一定的研究,文献[4]分析了线性系统下三种约束滤波算法,并利用车辆跟踪仿真实验比较了三者的性能;文献[5]将制约车辆运动的道路信息引入Kalman滤波模型,提高了滤波结果的精度. 但是,上述研究都主要集中于抗差自适应算法以及对残差的研究,即使考虑外部约束信息也多是在目标跟踪领域基于计算机进行二维仿真,将考虑附加约束信息的Kalman滤波与精密定位相结合并以实测卫星观测数据进行验证的研究较少. 鉴于此,本文讨论了一种利用先验基线约束信息对Kalman滤波进行改进的双站协同PPP定位方法,该方法在滤波解算过程中充分考虑了状态参数之间的函数关系,增强了模型的强度,不同程度上提高了定位解算的精度.

1 PPP数学模型

1.1 观测模型

传统PPP算法采用基于双频伪距和载波相位消电离层(IF)组合的观测方程[6]:

(1)

(2)

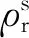
对于上述模型,电离层延迟项已经采用观测值IF组合的方式加以消除. 对流层延迟可分为天顶对流层干延迟和天顶对流层湿延迟,其中干延迟部分采用经验模型来改正,湿延迟部分通常作为参数来估计. 通常,与卫星相关的硬件延迟项会合并到卫星钟差项中,可通过IGS提供的精密钟差进行改正;与接收机相关的硬件延迟项会合并到接收机钟差中,作为一个整体进行参数估计. 相位观测方程中的相位延迟项(包含硬件相位延迟项和初始相位偏差项)会被相应的模糊度参数吸收,使得模糊度参数失去整数特性[7]. 相位缠绕、固体潮、大洋潮汐、相对论效应、地球自转等引起的误差根据相应的模型进行修正. 最终式(1)和式(2)经过误差改正后通常简写为:

(3)

(4)

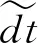
(5)

(6)

1.2 Kalman滤波参数估计

PPP中通常采用Kalman滤波算法进行参数估计,若待估的状态序列为{xk,k=0,1,…,n},观测值为{zk,k=0,1,…,n},则Kalman滤波模型可由如下线性化后的动态模型和观测模型表示[8]

xk=Fk-1xk-1+wk-1,wk-1～N(0,Qk-1),

(7)

zk=Hkxk+vk,vk～N(0,Rk-1).

(8)

式中:F为状态转移矩阵；H为设计矩阵；w和Q为系统噪声及其协方差矩阵,v和R为观测噪声及其协方差矩阵. 在静态定位中,状态向量主要包含接收机的位置(X,Y,Z)、接收机钟差dt、对流层延迟trop以及IF组合模糊度(Ni,i=1…，n)四类基本参数. 即:

(9)

状态转移矩阵F在静态定位中可设为单位阵.

设计矩阵H可表示为

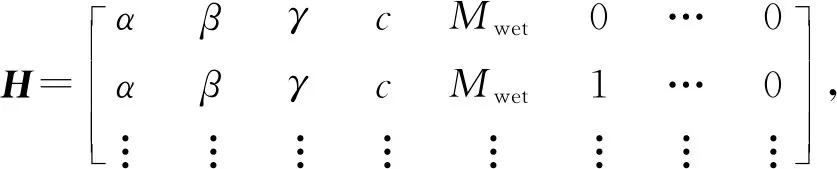
(10)

式中:α、β、γ为星站矢量的方向余弦;c为真空中的光速;Mwet为对流层延迟投影函数.其余为模糊度项系数.

观测噪声的协方差矩阵Rk可根据卫星高度角模型对伪距和相位观测值分别赋值,即:

(11)

过程噪声的协方差矩阵Qk为

(12)

式中,σ2为噪声对应的方差,可根据经验赋值.

对于静态PPP,位置参数和模糊度在过程噪声矩阵中对应的元素为0,接收机钟差对应的元素取105,对流层湿延迟参数对应的元素取10-9[9].

2 附加基线约束的双站协同PPP模型

2.1 附加基线约束信息的Kalman滤波

在实际的参数解算过程中,待估的状态参数间会存在一些已知的函数关系,这些先验的函数关系可以作为约束用来改善Kalman滤波的稳定性,从而增强PPP的定位性能[10].状态约束信息通常可表示为一系列的等式或者不等式,对于这些约束信息通常有以下几种处理方式:

1)模型简化法,通过引入等式状态约束来消除一些系统模型参数,从而简化模型;

2)伪观测法,将等式约束视为零观测噪声的高权重的完美观测值,使得观测方程得到增广,加强观测空间的结构[11],从而将约束估计问题转化为非约束估计问题. 批处理方法和序贯处理方法是伪观测法中常见的计算手段;

3)投影法,将未约束的Kalman滤波的状态估计投影到约束空间[12]. 事实上,上述三种约束处理方法具有等价性,前两种方法可视为投影法的特殊情况[13]. 为了便于理解状态约束对状态估计及其方差-协方差矩阵的影响,以下采用更一般的投影法的形式来推导附加约束的Kalman滤波递推公式.

系统的状态方程及观测方程如第1.2节的定义. 另外,等式状态约束条件通常表示为如下线性的约束方程:

Dk·xk=dk,

(13)

式中:Dk为系数矩阵;dk为约束向量.

利用投影法处理带约束的参数估计问题可表示为如下数学形式[12]:

(14)

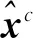
上述问题最优解为

xc=x-W-1DT(DW-1DT)-1(Dx-d).

(15)

当过程噪声和观测噪声为高斯的,可以取W的值为无约束条件下估值的误差协方差矩阵,即W=(Pk)-1,此时估计值具有最小的估计误差协方差.

采用投影法的约束Kalman滤波算法有两种形式,可分为开环形式和闭环形式. 具体区别在于,开环形式中,直接利用约束对最后的状态估计值进行改正,而闭环形式中,需要将每个历元修正后的估计值反馈给下一个历元. 两种形式的流程框图如图1所示. 由于闭环投影具有更好的约束性能[4],本文中采取闭环投影的形式.

(a)开环形式

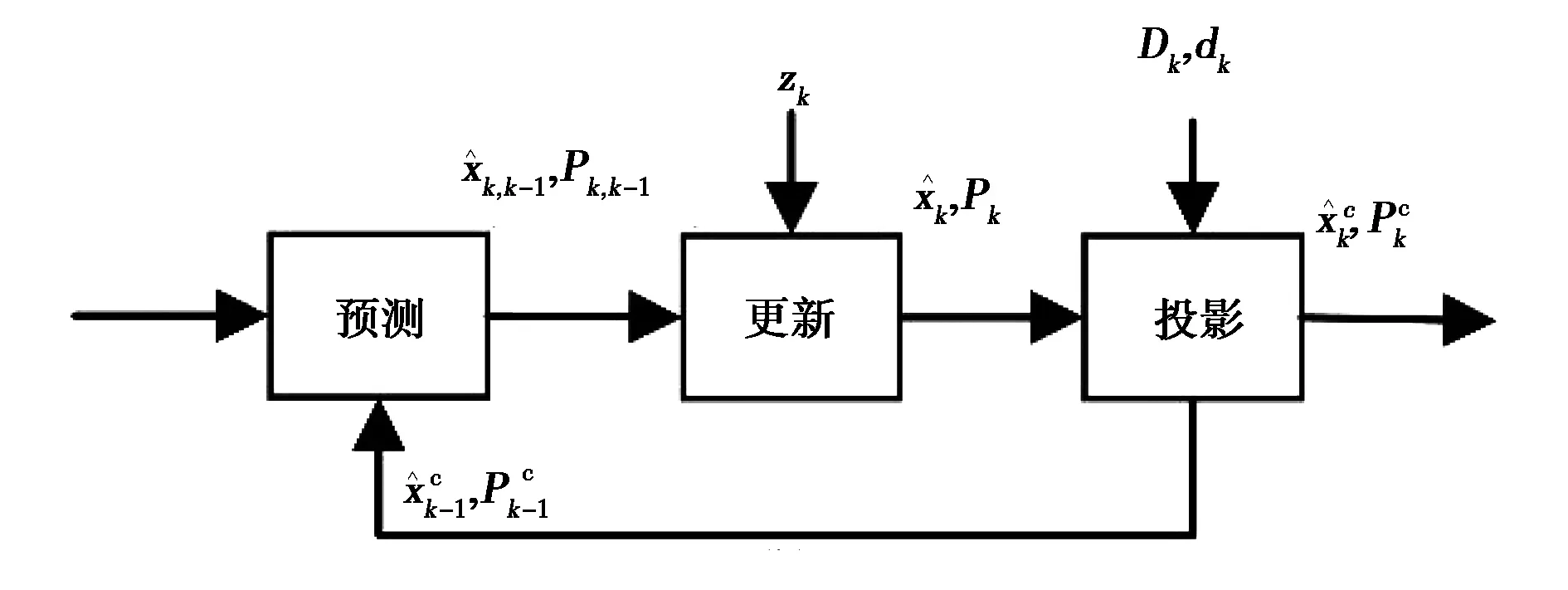
(b)闭环形式图1 投影法的不同形式

最终得到附加状态约束的Kalman滤波递推公式如下:

(16)

Pk,k-1=FPk-1FT+Qk-1,

(17)

(18)

(19)

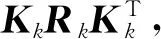
(20)

(21)

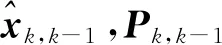
由上面的递推方程可以看出,将约束条件引入Kalman滤波方程,其思路是在原有滤波的基础上,利用约束条件对滤波递推方程中状态估值的表达式(19)作了修正,以改善滤波结果[10].

进一步研究约束修正后的估值的方差-协方差矩阵. 由式(21)可以得到:

(22)

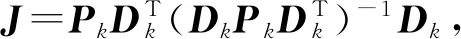
(23)

根据误差协方差的定义则有:

=Pk-JPk-PkJT+JPkJT.

(24)

根据J的定义,有如下性质PkJT=JPkJT,且JPk为正定矩阵,由式(24)可以进一步得到:

(25)

(26)

(27)

可以发现,经约束信息修正后的状态估值的误差协方差阵小于无约束条件下状态估值的误差协方差阵[14],即状态约束信息可以改善参数估值的误差-协方差矩阵,从而参数估值的精度得到了提高.

2.2 附加基线约束信息的PPP

考虑两个观测站同时进行静态PPP的定位场景,则这两个观测站之间会构成一个基线矢量,这个基线矢量不仅包含了方向信息也包含了长度信息. 因此,如果提前根据相对定位或者其他手段得到两测站的基线(相对位置坐标),则用各个方向上的相对位置坐标差除以基线长度可以获得这个基线矢量的方向余弦,即方向信息. 另外,根据基线坐标可以计算得到两个测站之间的距离信息. 上述方向和距离约束信息本质上提供测站之间的几何约束关系,将此几何约束信息融入到Kalman滤波解算就有可能提高每个测站的PPP定位性能.

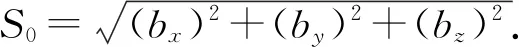
估值相对应的基线向量的基线长度为

(28)

首先,任何一个矢量的方向都可以由它的方向角来决定,而向量的三个方向余弦分别为这三个方向角的余弦值,因此可用矢量的方向余弦表征矢量的方向性. 设α,β,γ为基线矢量与地心地固坐标系三个坐标轴的方向角,cosα,cosβ,cosγ为对应的三个方向余弦,根据方向余弦的定义:

(29)

则任意k时刻,这两个测站位置参数满足如下方向约束:

(30)

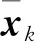
(31)

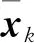
(32)

以X方向的基线方向约束方程为例,可写出矩阵方程Dk·xk=dk形式表示的基线方向约束:

Dk=

(33)

(34)

其他各方向上的基线方向约束方程构建方法同理.将得到的三个方向上的基线方向约束方程带入2.1节的Kalman滤波递推方程则可以得到方向约束后的两测站坐标.

此外,之前计算得到的两个测站之间的距离,也可以作为约束对两天线的位置进行修正. 两天线之间的先验距离为S0,则任意k时刻,这两个测站位置参数满足如下距离约束:

(35)

上述距离约束方程同样为非线性方程,需在预测值处进行线性化,只保留一阶项后可将上述方程整理为矩阵方程Dk·xk=dk的形式.有:

(36)

(37)

将上述方程带入2.1节的Kalman滤波递推方程则可以得到距离约束后的两测站坐标.

3 数据处理与分析

3.1 数据处理策略

本文以开源的PPP程序PPPH[15]为框架,根据附加约束的Kalman滤波算法原理对程序改进后进行PPP的解算. 数据预处理采用Turbo-Edit方法进行周跳的探测. 误差改正部分采用了IGS的精密产品和精化的误差改正模型来进行修正. PPP解算中未进行模糊度固定,参数估值为浮点解. 具体处理策略如表1所示.

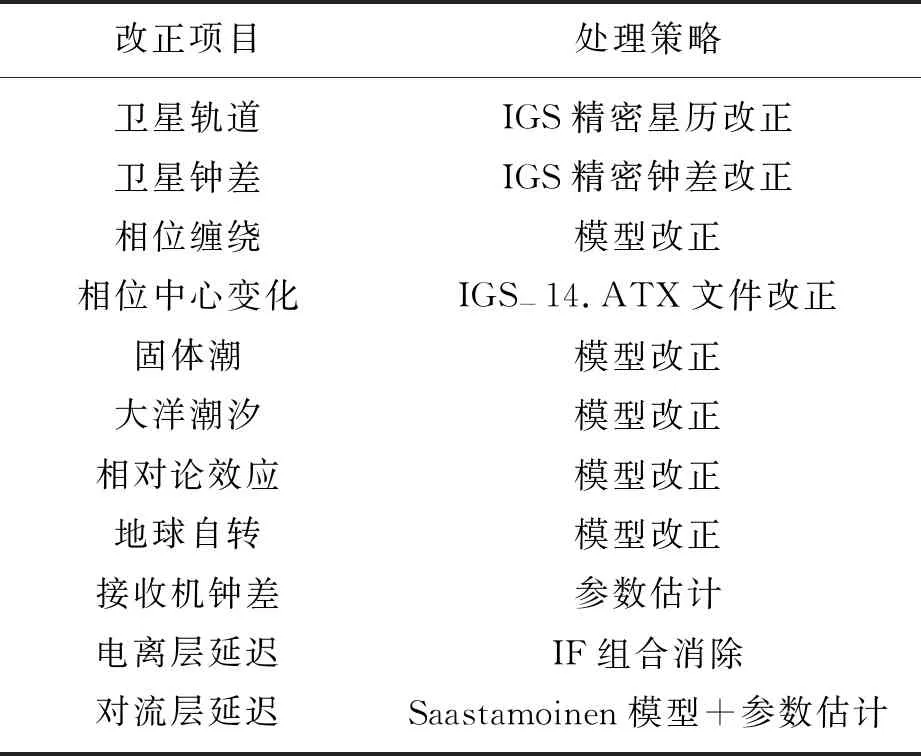
表1 数据处理策略

实验过程中采用15 min采样率的精密星历和30 s采样率的精密卫星钟差,并采用9阶拉格朗日内插对卫星星历和钟差进行插值加密,以获得每一观测时刻的卫星星历和钟差.

3.2 实验结果分析

为了更加全面地评估附加基线约束的PPP算法的定位性能,实验利用采集的真实GPS观测数据进行定位解算. 实验数据采集于山西省太原市中北大学校园内,接收机采用华测CHCNAV的接收机. 在相距位置约2.5 m的两个点分别架设两个天线,在同一时间段内对两测站进行同步观测,接收机采样率为1 s. 观测时间段为2020年1月2日6:39:26-9:18:15. 截取了其中三个不同时长的数据进行解算,分别为8:00-9:00的1 h观测数据;7:30-9:00的1.5 h观测数据;7:00-9:00的2 h观测数据.

为了确定方向约束和距离约束的约束方程的系数矩阵和约束向量,首先将观测数据利用RTKLIB软件static模式解得的基线作为两天线之间的约束. 解得的基线坐标为(-2.4597,-0.8604,-0.0028),基线长度为2.605 m. 以2.2节所述构建约束方程,得到约束方程后,依次采用以下四种方案进行PPP解算:

1) 采用不附加约束的Kalman滤波;

2) 采用附加基线方向约束的Kalman滤波;

3) 采用附加基线长度约束的Kalman滤波;

4) 采用同时附加基线方向约束和基线长度约束的Kalman滤波.

以两个天线在各个方向的定位偏差的RMS值为评价指标,评价两个天线在各个方向的定位精度. 各方向的RMS值由收敛时刻(CT)到观测截止时刻的坐标偏差计算得到,以连续60 s内三维坐标偏差的2范数不超过0.15 m作为判断收敛的条件. 得到如表2所示的三个不同时段内两天线X、Y、Z方向上的RMS统计.

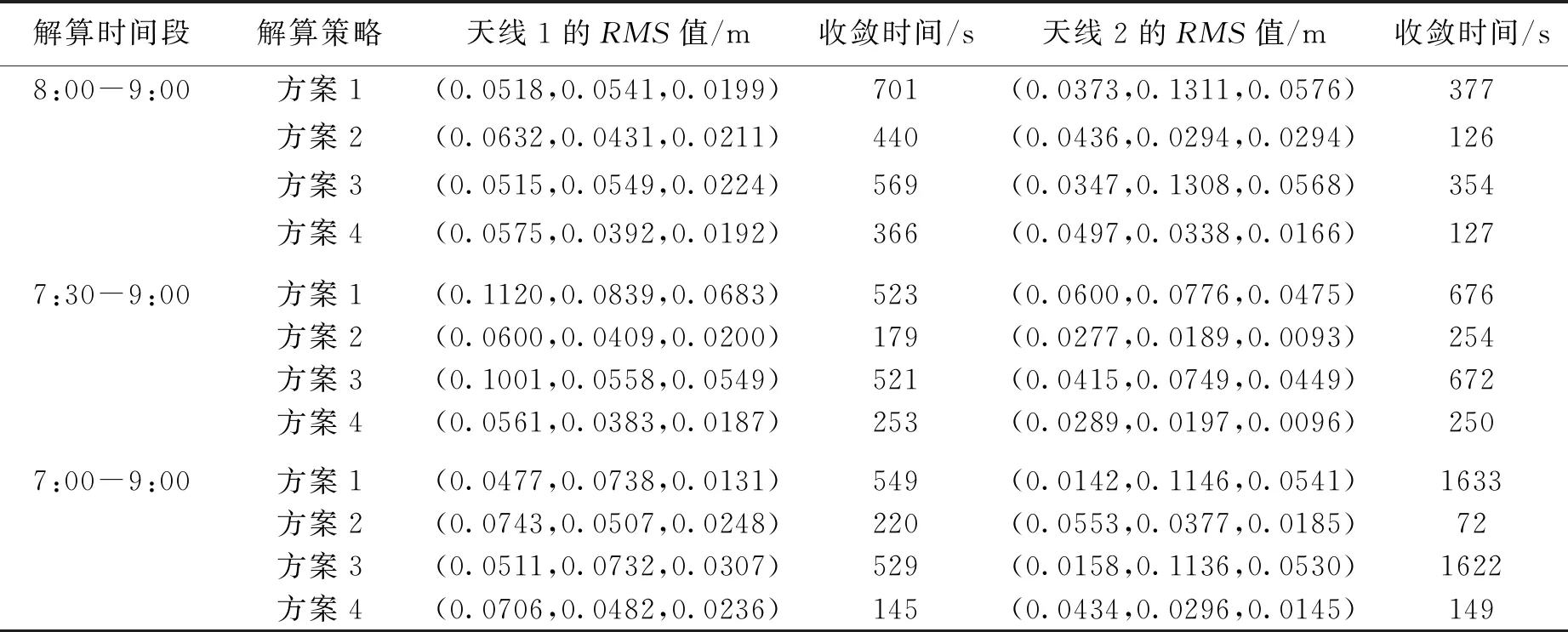
表2 两个天线定位偏差的RMS统计

分析表2可知,相比于方案1,参数解算过程中附加约束后(方案2～方案4),PPP定位性能得到了不同程度的改善,收敛时间也得到加快. 具体体现在:使用8:00-9:00时间段内数据进行解算,方案2下,1号天线Y坐标,2号天线Y、Z坐标估计精度得到提高,尤其是2号天线Y方向坐标RMS值由0.131 1变为0.029 4,减小了77%;方案3下,1号天线X坐标,2号天线X、Y、Z坐标估计精度得到提高;方案4下,1号天线Y、Z坐标,2号天线Y、Z坐标估计精度得到提高,同样2号天线Y方向坐标RMS值变化明显,由0.131 1变为0.033 8,减小了74%. 使用7:30-9:00时间段内的数据进行解算,三种附加约束信息的解算方案两天线各个方向上定位精度均得到提高. 使用7:00-9:00时间段内的数据进行解算,方案2下,1号天线Y坐标,2号天线Y、Z坐标估计精度得到提高,特别是2号天线Y方向坐标RMS值由0.114 6变为0.037 7,减小了67%;方案3下,1号天线Y坐标,2号天线X、Y、Z坐标估计精度得到提高;方案4下,1号天线Y坐标,2号天线Y、Z坐标估计精度得到提高,同样2号天线Y方向坐标RMS值变化明显,由0.114 6变为0.029 6,减小了74%.

综合来看,通过在PPP解算中附加约束条件,能有效缩短收敛的时间. 不同观测时长的数据,利用附加约束的PPP解算方案进行解算,收敛时间都得到了缩短. 尤其是方向约束条件(方案2及方案4),对于收敛时间改善效果较为明显. 三种附加约束的解算方案,均能较大程度提高2号天线Y方向的定位精度. 另外,采用1 h和2 h观测时长的数据,不同解算方案下,三个方向上定位精度变化不同,但总体上三维方向坐标估计偏差呈减小的趋势,这点从收敛的判定条件和收敛时间缩短中也可以看出来. 总的来看,三种附加约束的PPP算法定位性能均满足精密定位的要求,相比无约束定位算法,在不同方向上有不同的提升效果.

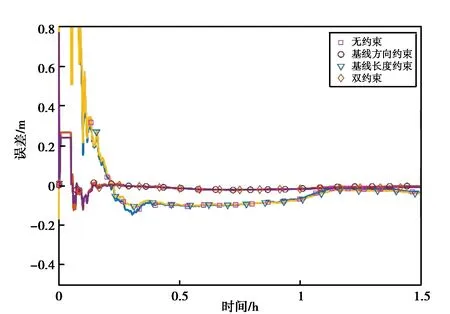
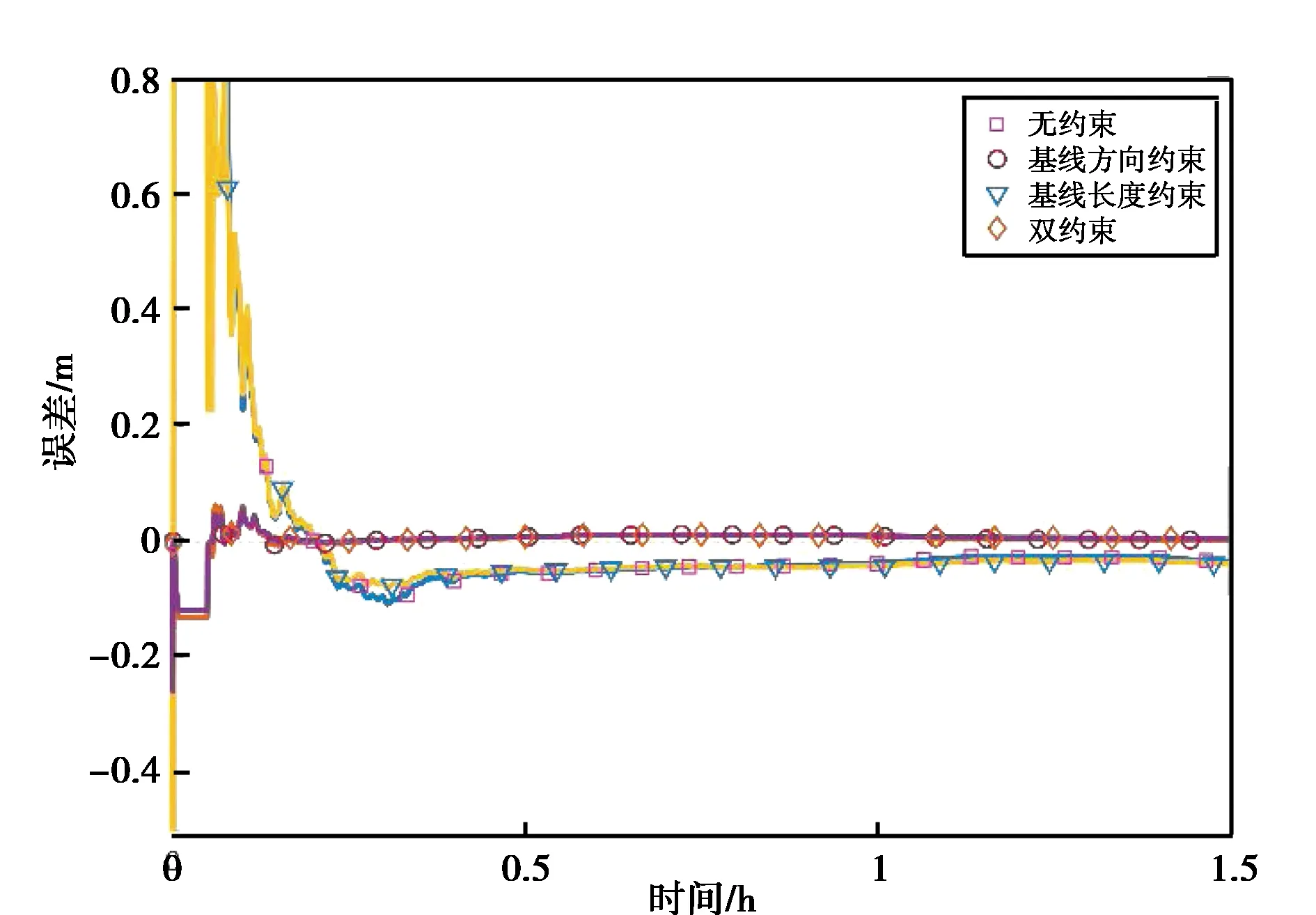
为了观察约束条件对于参数估计的影响过程,将7:30-9:00这一时间段四种方案的解算结果同RTKLIB的PPP模式解得的位置坐标(视为真值)进行比较,可以得到三个方向上4种解算方案的坐标估计误差变化,如图2所示.

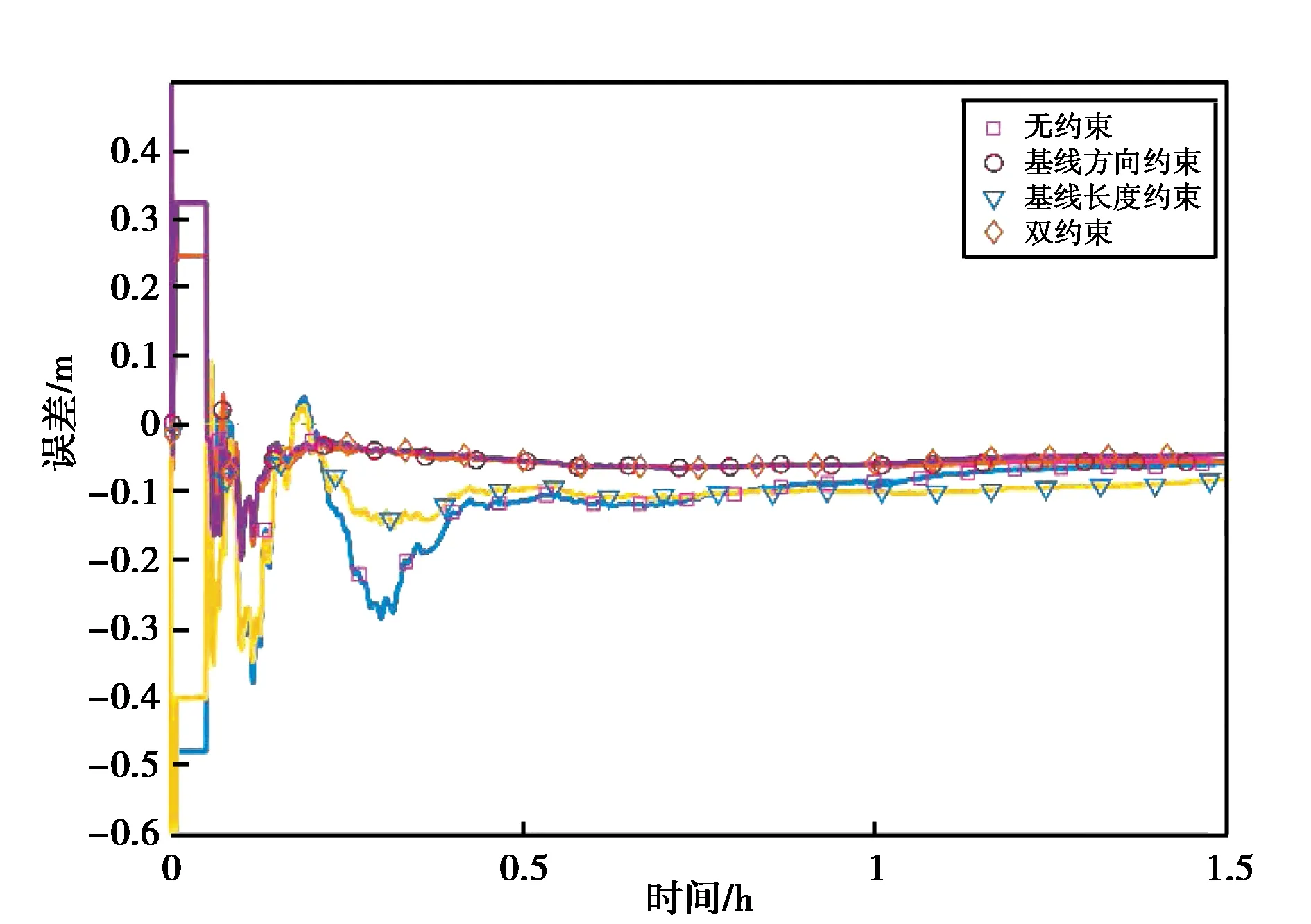
(a) 天线1-X方向

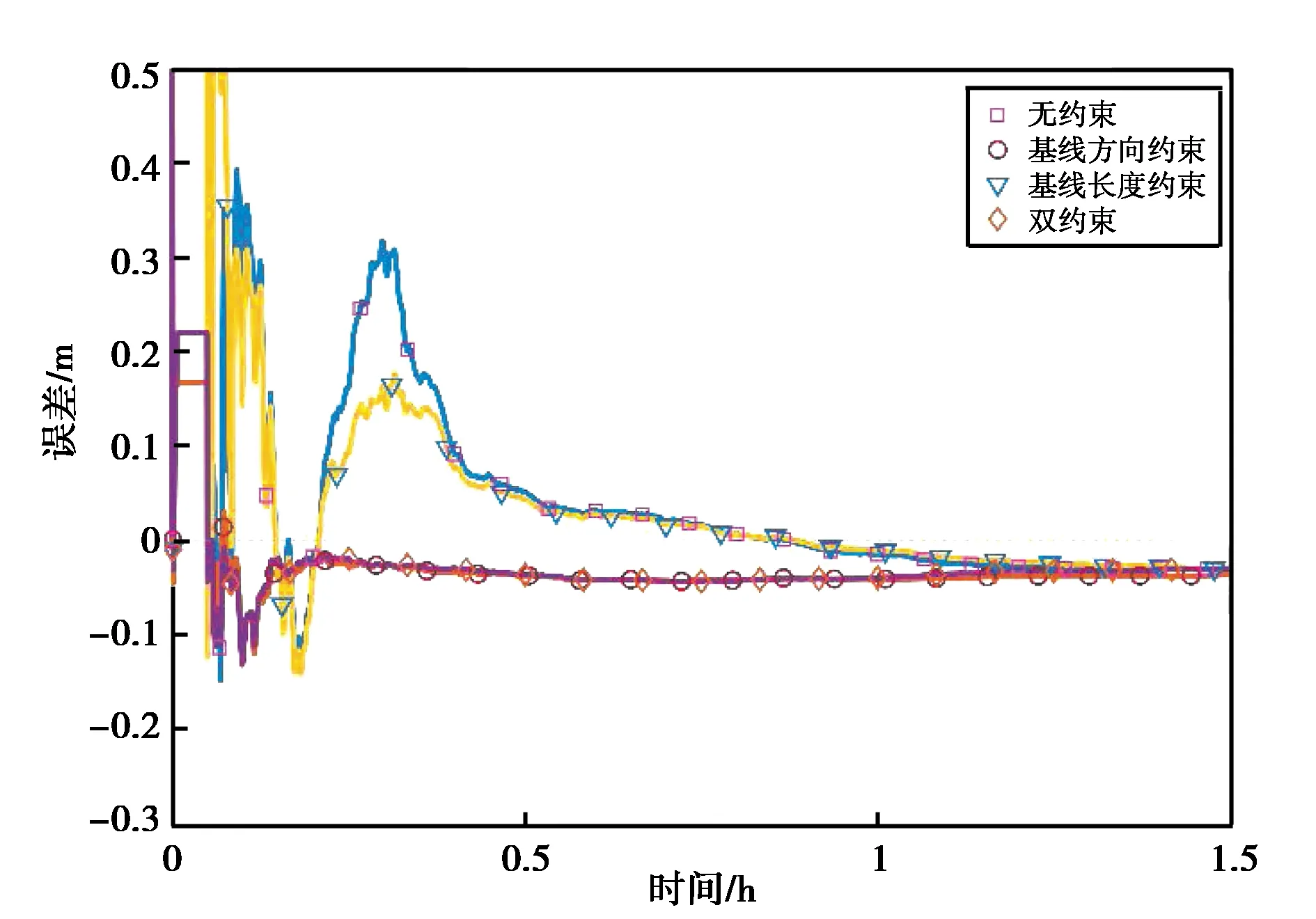
(b) 天线1-Y方向

(c) 天线1-Z方向

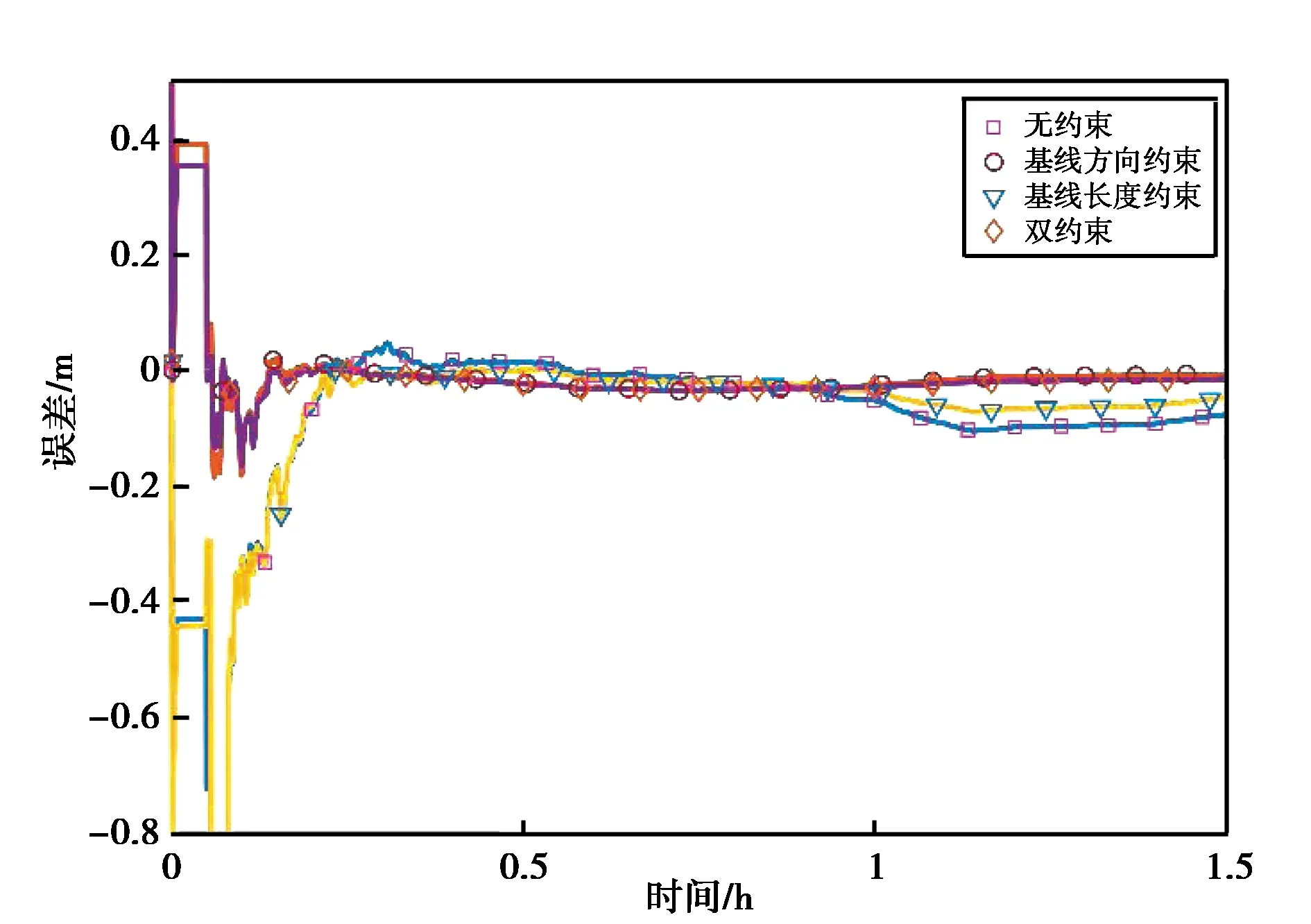
(d) 天线2-X方向

(e) 天线2-Y方向

(f) 天线2-Z方向图2 不同解算方案坐标估计误差

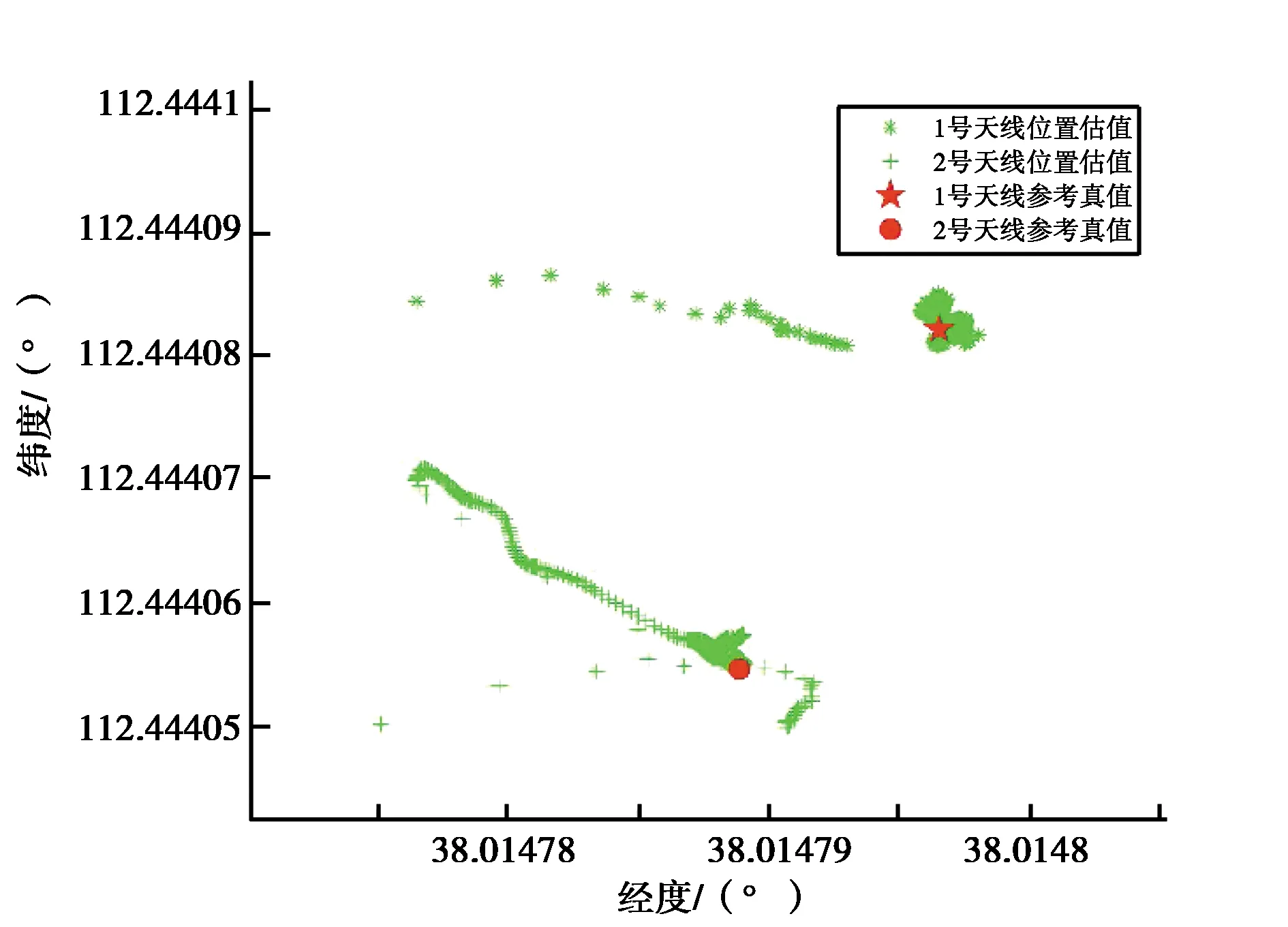
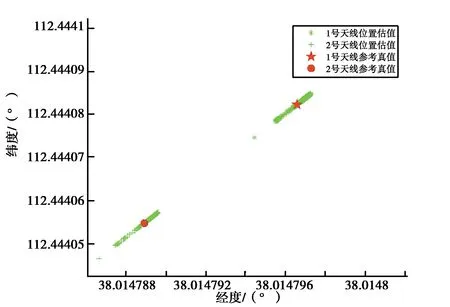
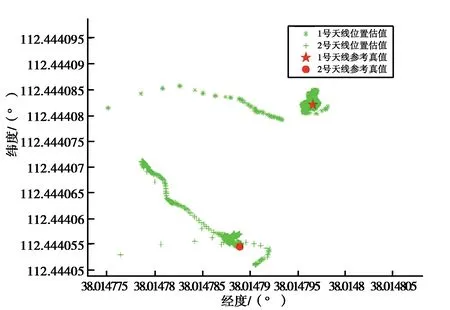
另外,将解得的两天线位置坐标转换到大地坐标系下,可以得到上述4种解算方案下的两天线估计位置分布,如图3所示.

(a) 方案1

(b) 方案2

(c) 方案3

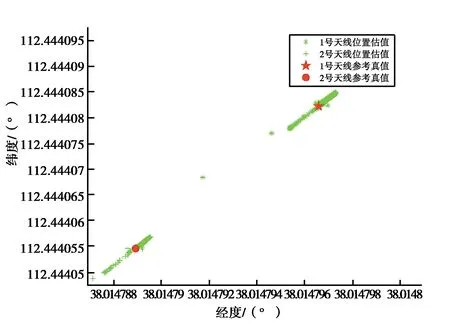
(d) 方案4图3 大地坐标系下两天线位置分布散点图

对比图2中不同方向上4种解算方案的位置估计误差图可以发现,附加约束的PPP解算结果(方案2、方案3、方案4)的精度都不同程度优于无约束的PPP解算结果. 可以发现,不同方向定位结果收敛稳定之前,附加约束的解算方案误差曲线相比无约束解算方案更加平缓,其对应的定位误差更小,而估计结果稳定后,4种方案的误差曲线差距并不明显. 说明约束条件主要影响前期解算精度不高的时段,通过附加约束能够较快使坐标估计值符合到真值处,降低定位误差,从而提高收敛速度. 待解算收敛后定位达到较高精度,约束条件对于估值的作用削弱.

对比图3中的天线位置散点图可以发现,无约束时估计得到的天线位置分布较为散乱,具有很大的随机性. 附加约束后(方案2、方案3、方案4),天线位置分布均产生变化,尤其是方案2及方案4附加方向约束的情况下,得到的天线位置分布具有很强的规律性,估计得到的天线位置分布在两天线所在直线上. 这也体现了约束条件对于接收机位置估值产生了影响.

另外,综合对比表2、图2～3可以发现,当仅考虑距离约束(方案3)的情况下,其定位精度提升并不明显,估计得到的天线位置分布仍近似于无约束的参数估计结果,较为离散. 而在附加基线长度后,另外附加约束方向约束(方案4),对于解算结果影响较大,其最终的接收机定位分布接近于仅考虑基线方向约束的情况,并且两天线Y方向定位精度提高不大的情况得到了有效改善. 究其原因可能是因为PPP作为一种精密定位手段,该技术本身的定位精度很高(本实验中无约束下为厘米级),而RTKLIB相对定位解算出的基线,其精度也在厘米级,因此通过基线坐标求平方和得到的距离约束条件对于两个天线的坐标改正量较小. 而基线方向约束条件隐含的几何约束效果对于两个天线的坐标改正量较大. 在构建约束条件时,特别要注意先验信息要足够精确,其精度最好高于无约束定位结果1到2个数量级,可使得约束效果更为明显. 如可通过采集更长时间的观测数据或者采用双差定位的方式,求得毫米级的先验点坐标信息,从而获取更准确的基线信息.

4 结束语

针对PPP中采用Kalman滤波进行数据解算时,其性能受限于动态模型和滤波初值的准确程度的情况,本文提出将待估参数之间的函数关系作为约束应用到滤波解算过程中以改善定位性能. 通过实测的GPS观测数据进行实验发现,附加天线之间所成基线隐含的方向信息和距离信息,可以不同程度地提高传统PPP的定位精度,缩短收敛时间. 但是同样发现,由于约束条件本身精度的限制,限制了约束条件对于参数估值的修正作用. 因此,首先需要保证事先获得的约束信息有较高精度,从而建立准确的约束条件;另外在选取约束条件时,应更仔细地分析系统本身的特点,找到约束效果更强参数间的函数关系,如直线轨迹约束强于距离约束和平面约束,这是保证约束定位算法解算性能的前提.