资本资产定价模型的实证分析——以单只股票为例

(四川大学 四川 成都 610000)

一、理论基础

价格机制是市场机制的核心，而金融产品的定价理论一直是金融理论的焦点。威廉·夏普(William Sharpe)通过对马科维茨模型的进一步分析后进行简化，于1963年提出了单因素模型。次年，夏普提出了资本资产定价模型(CAPM， Capital Asset Pricing Model)。该模型主要通过公式中的β系数衡量资产风险，使得资产风险可以定量计算。在此之前，由于理论的限制，大多数研究者只能对资本市场理论进行理论上的定性分析，而资本资产定价模型的剔除使其转入定量分析。投资者得以运用证券投资理论进行实际投资操作。

CAPM模型自从诞生以来，国内外的众多学者对该模型进行了研究和改进。经过不断完善，资本资产定价模型在风险分析、资产定价等领域得到了广泛应用。模型中的β系数用来衡量资产的系统性风险。该模型适用于单一证券或投资组合。模型中的β系数的绝对值越高，则表示该证券或投资组合收益率的波动率相比于整体市场越大。若β=0，则表示该证券或投资组合的收益率与无风险收益率相等。一般情况下，β>0。当0<β<1时，市场整体的波动率高于该证券或风险资产组合的波动率；β>1时，该证券或投资组合的波动率小于整体市场波动率。β<0这种情况从理论上说也是存在的，说明该证券或投资组合的收益率变动情况与市场整体成反方向。大部分股票的β系数在0.5～1.5之间。

二、实证研究和结果

(一)数据选取

本文选取2010年-2019年数据，共10年作为研究对象，所采取的数据均为日度数据。所用数据来源于国泰安数据库。使用R语言数据分析软件进行数据的整理和分析。

本文主要选择A股市场某公司(下称A公司)股票。A公司属港口水运行业，于2009年在上证股市上市。本文选择国泰安数据库中考虑现金红利再投资的日个股回报率字段作为个股收益率数据，用rA表示。本文选取的无风险收益率数据为国泰安数据库中“日度化无风险利率”字段作为无风险收益率，用rf表示。对于市场整体收益率，本文选取“考虑现金红利再投资的综合日市场回报率(流通市值加权平均法)”为市场整体收益率，使用rm表示。

(二)模型构建

将A公司股票收益率数据和上证市场整体收益率导入软件中进行拟合，得到该公司的公司个股收益率和整体市场组合收益率的散点图和最佳拟合曲线，如图1所示。

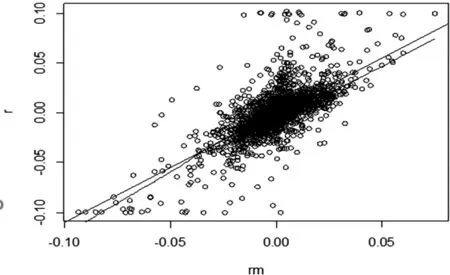
图1 A公司股票收益率和整体市场收益率散点图

根据上图可以看出，该公司股票十年内的收益率与整体市场收益率大致满足线性相关关系，并且为正相关。根据CAPM模型的推广式和上述分析可以构建出该公司β系数的一元线形回归模型：

rA-rf=β(rm-rf)+ε

整理后可以得到β系数计算公式：

ε为模型的随机误差项

(三)参数估计

应用前一节得到的方程模型，应用R语言数据分析软件对数据进行回归分析，得到β系数，回归结果如表所示：

表 2 β系数回归结果

从上表可以看出，回归系数为1.093，且在1%的水平下显著，拒绝原假设，自变量对因变量有显著影响。回归方程斜率为1.093，说明该公司β系数为1.093。说明整体市场收益率每上升1%，该公司收益率将上升1.093%，反之也将下降相同百分比。该公司β系数略大于1，投资者在选择该公司进行投资时还是存在一定风险。

三、小结

根据分离定理，系统风险决定了资产的收益率。资本资产定价模型的提出，使得投资者可以估计出β系数，对资产定价和投资风险分析有重要意义。本文经过理论与实证分析，对A公司的β系数进行测算。运用图形分析和数据分析探究该公司收益率和整体市场收益率的关系，并得到其β系数，本文得出的结论如下：

(1)从散点图和拟合线可以看出，该公司收益率与整体市场收益率成正相关关系。

(2)通过对数据进行回归分析得到，该公司的β系数为1.093，略大于1。该公司收益率波动性略大于上证市场整体收益率，其风险也略高于整体市场。投资者在进行投资时仍需要慎重选择。

资本资产定价模型的假设十分严格、理想。虽然可以在一定程度上解释收益率变动情况，但其缺点也十分明显。因此，在进行实际操作过程中，仍需要进一步完善模型，更加综合全面的分析。